冲击地压预测是冲击地压灾害防治的基础[1-6]，目前开采中的冲击地压预测主要基于冲击地压孕育过程中的应力、变形、钻屑、微震、电磁辐射和电荷等指标数据，分析指标演化规律，建立单指标[7-8]或多指标[9-11]方法进行预测。一方面，冲击地压失稳破坏过程是临界不稳定状态，力学行为是非线性和不规律的，不仅应力、变形等力学指标，而且电磁辐射、红外辐射等物理指标随时间变化均呈现出非单调性[12-17]特点，另一方面，冲击地压发生的地质环境差异、构造复杂、类型多样，冲击地压前兆具有复杂性和多样性。因此，冲击地压预测的临界指标确定困难。针对冲击地压预测的非线性科学问题，只有动态监测、跟踪非线性破裂的发展过程[18]，识别煤岩变形破坏状态和特征，才有可能达到精确预测的目标。
在岩爆、冲击地压和滑坡等工程地质灾害的微震观测发现，灾害发生前，微震事件数量会逐渐增多，并会向某一区域集中，密度增大，认为微震事件的聚集是工程地质灾害的前兆特征[19]。微震是岩体内部微裂纹发生和扩展演化的反映，微震聚集的本质是煤岩受载作用下产生微裂纹，当加载到一定阶段，原来随机分布的微裂纹会集中在一个或多个条带上发展，即形成所谓的微裂纹局部化；自微裂纹局部化开始，煤岩力学行为便步入了非线性、不连续的阶段，微裂纹局部化演化的结果是宏观裂纹的出现和快速扩展，直至发生破坏，这就是变形局部化现象。变形局部化现象作为煤岩非线性破裂发展过程中的必经阶段和破坏前兆特征，成为工程地震灾害预测研究的重要内容[20]。
在变形局部化演化规律及破坏特征识别方面。如郑捷等[21]用光弹贴片法、声发射技术和电视录像的方法，研究了辉长岩试件在单轴压缩过程中的变形局部化；潘一山等[22]采用数字散斑相关方法，研究了岩石变形局部化演化过程，并得到了变形局部化带宽度；马少鹏等[23]通过引入非均匀性指标，提出了变形局部化启动的识别方法；宋义敏等[24]通过实验研究了变形局部化的变形场和能量演化规律，得到局部化带相对滑移速率与声发射参数对应关系。
在跟踪变形局部化过程研究冲击地压发生规律方面，LINKOV等[25]根据变形局部化过程具有单调增加、可跟踪性的特点，提出采用变形局部化理论和实验方法进一步研究冲击地压。章梦涛等[26]认为煤岩体变形局部化，形成应变集中区是冲击地压发生的必要条件；潘一山[27]研究了冲击地压启动后煤岩变形破坏规律，发现冲击地压启动后煤岩变形破坏产生局部化。
虽然学者们在变形局部化预测冲击地压方面进行了初步探索，但以下3个方面问题需要进一步研究和探讨：① 没有明确变形局部化与冲击地压之间的关系，缺乏变形局部化预测冲击地压的理论依据。② 无法从理论上描述冲击地压孕育发展和相对应的变形局部化过程。因为传统的弹塑性本构关系不含有长度的参数，在进行理论模型研究时，不能给出变形破坏向某一区域集中，且集中区具有一定尺度的现象。③ 国内外对于实验室煤岩试件破坏、隧洞岩爆、煤矿冲击地压都观测到了变形破坏具有变形局部化特征，但是如何来量化变形局部化状态还没有提出。
本文研究变形局部化与冲击地压的关系，提出描述变形局部化的本构模型，计算变形局部化带的大小，通过与实验结果对照确定煤岩本构参数。提出局部化状态参数描述方法，室内试验采用声发射局部化预测试件破坏区域，对煤矿现场采用微震局部化预测冲击地压危险区域。
1 煤岩变形局部化预测冲击地压基本原理
通过理论推导，建立冲击地压发生与煤岩变形局部化的对应关系，为变形局部化预测冲击地压提供理论依据。
1.1 冲击地压发生临界条件
煤矿矿井中发生在煤体中的冲击地压，多数是由于煤岩体在压性载荷下发生的失稳[28-29]。
设煤岩变形系统在面力P和体力F的作用下，产生的位移为u，应力为σ，应变为ε，塑性软化区大小为Vs，其余的弹性区大小为Ve。设在某一平衡状态下，给煤岩体施加一个微小的虚位移Δu，产生虚应力Δσ，虚应变Δε，若外力所做的虚功大于应变内能的增加，则煤岩变形系统是非稳定的，即冲击地压发生条件为
(1)
由于煤岩系统处于平衡状态，满足虚功方程，即外力在虚位移所做虚功等于应力在虚应变所做虚功，方程可以表示为
(2)
由式(1)和式(2)简化，可得到冲击地压发生条件为
(3)
1.2 煤岩变形局部化发生条件
煤岩变形系统在面力P作用，产生的应力为σ，应变为ε。部分区域由于应力集中超过峰值强度而变成应变软化材料，该部分的区域为Vs，其他区域仍为弹性变形区，体积为Ve。在该状态下假设煤岩系统面力载荷产生一个扰动增量ΔP，则产生应力增量Δσ，应变增量Δε，位移增量Δu，则
(4)
式中，B为应变矩阵。
而Δε和Δu的关系为
Δε=BΔu
(5)
弹性区煤岩本构关系为
Δσ=DeΔε
(6)
软化区煤岩本构关系为
Δσ=DepΔε
(7)
式中，De、Dep分别为弹性矩阵和弹塑性矩阵。
将式(5)～(7)代入式(4)得
ΔP=KΔU
(8)
(9)
式中，K为刚度矩阵；ΔU为总体位移向量。
根据变形局部化定义，假如在同一增量ΔP作用下，还存在另一组与ΔU不同的位移增量分布，则该点即为破坏局部化开始点。设在ΔP作用下，产生的另一组位移分布为ΔU*，则有
ΔP=KΔU*
(10)
比较式(8)和式(10)有
KΔa=0
(11)
式中，Δa=ΔU-ΔU*，为2个不同位移场分布之差。
当式(11)存在非零解时，则有2个位移分布存在，即破坏局部化开始，而式(11)存在非零解的条件为
det K=0
(12)
{ΔU}TKΔU=0
(13)
(14)
可见煤岩体破坏局部化开始条件和煤岩体冲击地压发生的临界条件是一样的，煤(岩)体应力接近强度极限，破坏局部化，产生应变集中区，微裂隙在区内进一步密集并合，形成宏观裂隙。当宏观裂隙扩展，发生失稳扩展时，猛然释放弹性能就发生冲击地压。平衡系统重新恢复稳定，裂隙扩展停止或减速趋于稳定，冲击地压现象终止。这就是从煤(岩)体破坏的角度，所看到的冲击地压发生的物理过程。
因而可以说冲击地压的变形破坏过程就是煤岩体破坏局部化的过程。
2 煤岩变形局部化解析分析
采用梯度塑性理论，通过引入内部长度参数，构建变形局部化模型，对变形破坏向某一区域集中，且集中区具有一定尺度的现象进行理论解析。
2.1 煤岩塑性变形的非局部性
传统的宏观连续介质力学是局部的理论，即一个物质点上的应力被认为仅和该点过去的变形历史有关。而事实上，材料中一个物质点的状态受到周围点发生变形的显著影响，尤其对于煤岩材料，影响其力学性质的主要因素是颗粒直径分布及裂隙的发育情况等，因此产生塑性变形时是非局部的。材料的本构关系不仅和应变有关，而且与应变梯度有关，即
(15)
式中，
为应变梯度，为了将其与第1项ε统一量纲，必须引入一个长度量纲形成
为材料内部长度参数，大小反映了材料非局部作用的尺度。对于粒状煤岩，l的大小和粒径相当，对于裂隙煤岩，l的大小与裂隙尺寸相当。
实际上，
其中，L为与变形相关的特征尺度，对于通常的煤岩变形问题，L≫l，则
因此忽略梯度效应的传统理论是足够的。当煤岩产生破坏局部化时，煤岩变形局部化特征尺寸L≈l，此时应变梯度和应变是同量级。因此，研究煤岩变形局部化时，必须考虑应变梯度的影响。
2.2 煤岩变形局部化的应变梯度模型
研究煤岩变形局部化问题，在屈服函数中考虑二阶塑性应变梯度项，并引入材料内部长度l，建立煤岩变形局部化的应变梯度模型。图1为煤岩应力应变曲线(图中，σc为峰值应力；εc为峰值应变)。
图1 煤岩应力应变曲线
Fig.1 Stress-strain curve of coal and rock
在弹性阶段，煤岩的本构关系为
σ=Eε
(16)
达到峰值强度后，煤岩进入应变软化的塑性变形，考虑煤岩的应变梯度，根据各向同性假设，应变梯度只能是偶次阶，取简单的二阶梯度，屈服函数形式为
(17)
式中，
为屈服应力;εp为塑性应变。
2.3 煤岩变形局部化区域带宽的解析解
煤岩变形局部化会达到什么程度？尺寸多大？和煤岩材料性质有什么关系？下面进行理论推导。
弹塑性小变形问题为
(18)
式中，
为总应变率向量；
为弹性应变率向量；
为塑性应变率向量。
定义等效应力σi及等效塑性应变率
为
(19)
式中，σ′为偏应力向量。
煤岩材料符合Drucker-Prager屈服破坏准则：
(20)
式中，I1为应力第1不变量；J2为应力偏量第2不变量。
式中，φ为煤岩材料内摩擦角。
单轴压缩下岩石本构关系简化为双线性。峰值强度前为线弹性，弹性模量为E。超过峰值强度σc后，线性应变软化，软化模量为λ。假设在一般应力状态下屈服应力
和等效塑性应变γ满足单轴时的本构关系，则
(21)
考虑各向同性的煤岩材料，因而只能引入偶次阶的梯度塑性项，取最低的二阶梯度。假设屈服应力与等效塑性应变二阶梯度∇2γ成线性关系，则
∇2γ
(22)
则屈服函数F写为
∇2γ=0
(23)
假设煤岩材料符合相关流动法则
(24)
式中，
为塑性乘子率。
设Q=diag[1,1,1,1/2,1/2,1/2]，则
(25)
引入对称矩阵P：
则屈服函数及塑性应变率向量分别为
∇2γ
(26)
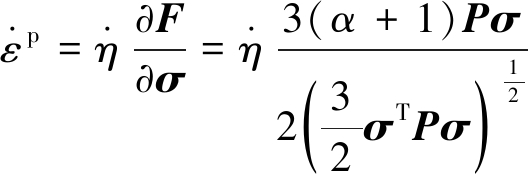
(27)
(28)
式中，
考虑梯度塑性的增量本构关系变为
(29)
式中，De为弹性矩阵。
在试验机具有极大刚度、加载速率极小的条件下，煤岩试件-试验机系统可简化为图2所示的模型。
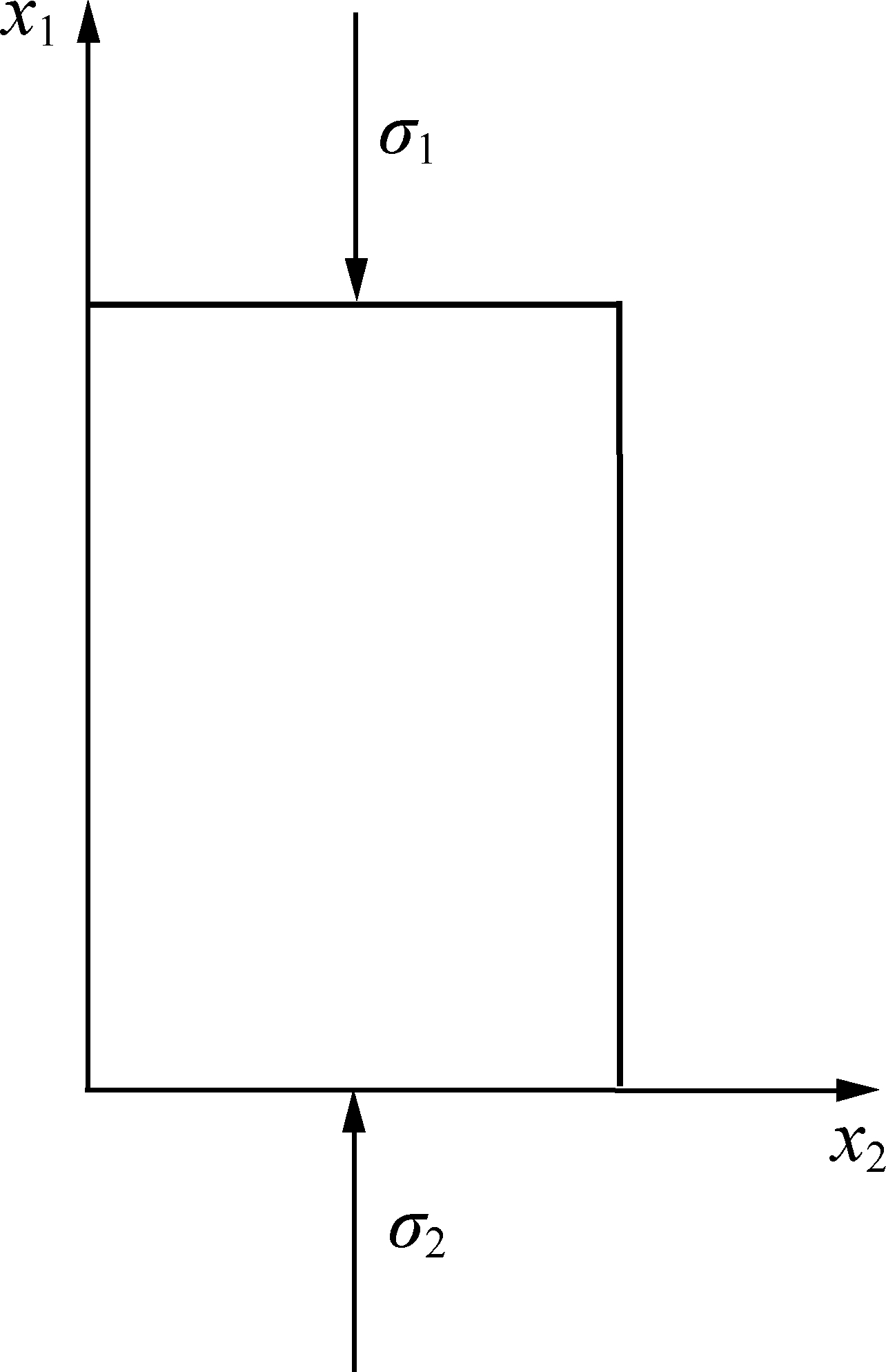
图2 煤岩试件-试验机系统冲击地压模型
Fig.2 Rockburst model of coal rock specimen-testing machine system
平面初始应力状态：
σ={σ11,0,σ33,0,0,0}
(30)
式中，σ33=0对应于平面应力单轴压缩，σ33=0.5σ11对应于不可压缩平面应变。
对于单轴压缩平面应力情况，根据平衡方程，并考虑局部化变形区产生体积扩容，假设具有关系：
(31)
式中，δ为煤岩材料的扩容系数，δ=1退化为不可压缩情况。
引入流函数φ得到平面应力情况下的应变率：
(32)
(33)
对屈服条件取全微分得到一致性条件，将应变率代入得出方程组：
(34)
(35)
(36)
(37)
式中，下标1、2代表x1、x2方向；ν为泊松比；G为剪切弹性模量。
假设煤岩材料在如图3所示的坐标系下出现宽度为W的变形集中区，其倾角为θ，局部化区域外围还是弹性变形区。引入垂直于局部化带的坐标系xoy，则有坐标变换：
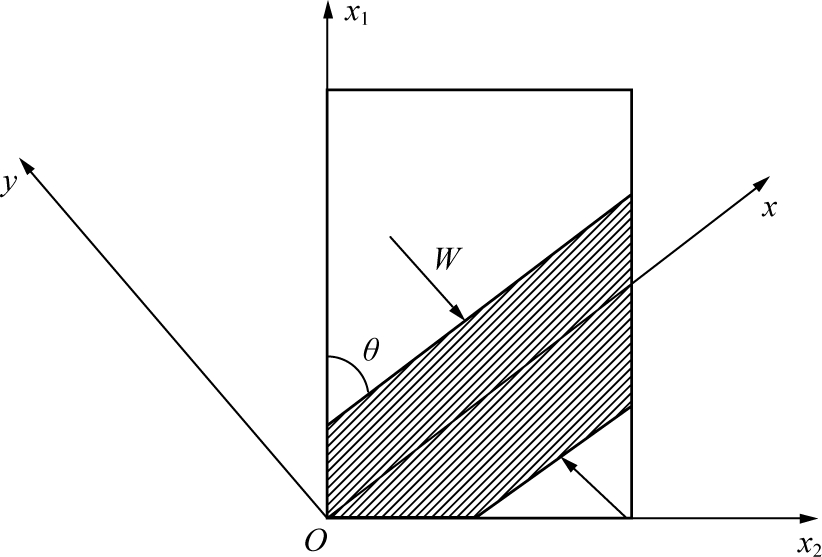
图3 煤岩变形局部化带及坐标变换
Fig.3 Localization zone and coordinate change of coal rock deformation and failure
x=x1cos θ+x2sin θ，y=x1sin θ-x2cos θ
(38)
假设变形局部化带内参数沿着x方向不变化，是均匀的，只沿着变形局部化带的y方向变化，则
(39)
(40)
(41)
(42)
(43)
根据坐标变换，式(34)和式(35)简化为
(44)
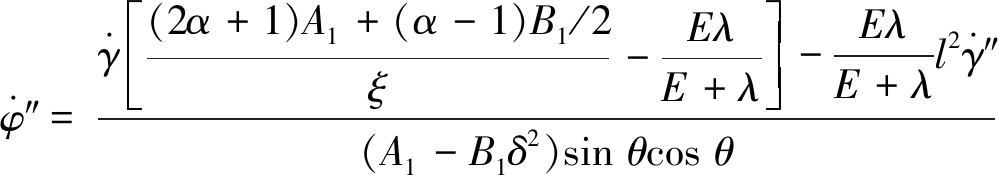
(45)
从上面两式中消去
得
(46)
(47)
在局部化带和外围的弹性区交界上应有边界条件：
(48)
要使微分方程(45)的解满足边界条件，即能形成变形局部化带，则系数A必须满足：
A=a2>0
(49)
分析A的表达式可知E、G、λ、l都是材料常数，仅θ是变量，要使A满足式(44)，则必须使A取极大值，由此得局部化带的角度θ为
(50)
局部化带的宽度为
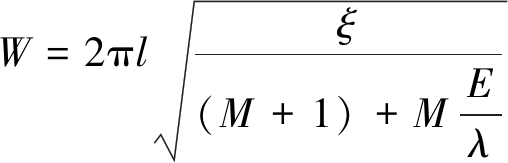
(51)
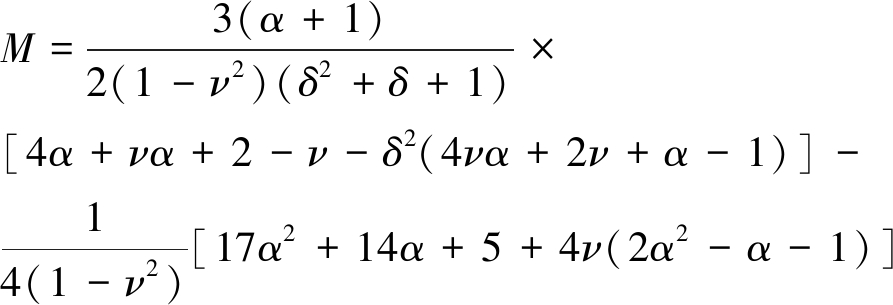
(52)
由上述分析可知，采用梯度塑性本构关系，煤岩试件-试验机系统发生冲击地压后煤岩出现变形集中区，根据计算得出了上述的局部化带宽度的计算公式。煤岩发生冲击地压后变形破坏将完全集中在此，其他区域还处于非破坏状态。
以煤(岩)的弹性模量为3 GPa，内摩擦角为30°，泊松比为0.3，煤(岩)冲击能指数(双线性模型中其表达式为E/λ)为1为例，计算材料内部长度与局部化带宽度关系曲线如图4(a)所示。以煤(岩)的弹性模量为3 GPa，内摩擦角为30°，泊松比为0.3，内部长度为1 mm为例，计算冲击能指数与局部化带宽度关系如图4(b)所示。
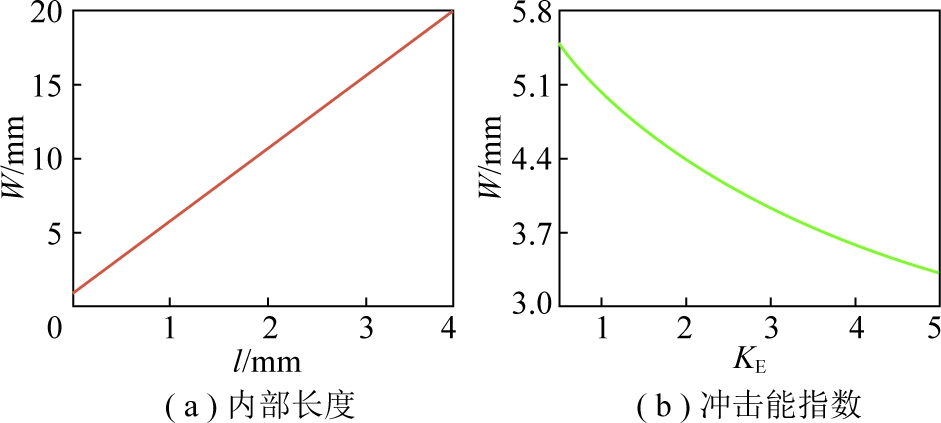
图4 变形局部化带宽度W的影响因素
Fig.4 Factors influencing the width W of deformation damage localization zone
根据上述解析分析可得，随着材料内部长度l增大，局部化带宽度W线性增大；随着冲击能指数E/λ增大，局部化带宽度W非线性减小。
3 煤岩变形局部化室内试验研究
通过开展煤岩变形破坏单轴压缩加载试验，采用数字散斑方法结合变形局部化带宽度的理论公式，计算并分析煤岩的材料内部长度参数。
实验系统由实验加载系统和数字散斑相关方法观测系统2部分组成。实验加载系统为RLJW-2000型液压伺服试验机，以位移控制方式进行单轴压缩加载，采集加载过程中载荷信息。数字散斑相关方法观测系统的测试和数据分析由硬件和软件系统两部分组成。硬件系统由CCD相机、光源、计算机组成。实验系统如图5所示。
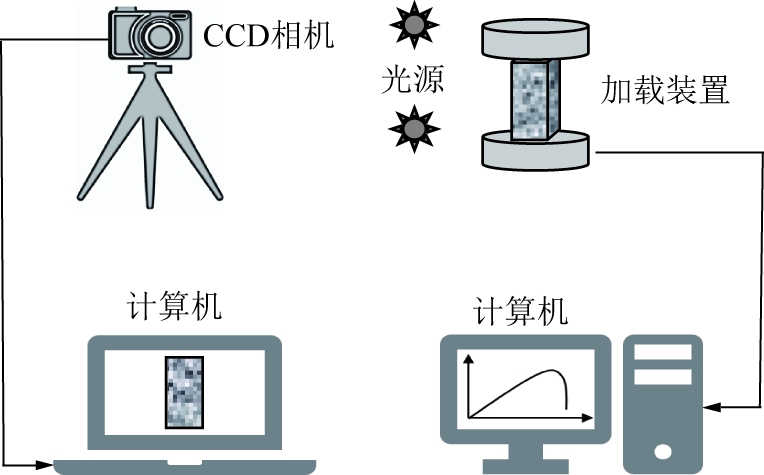
图5 实验系统示意
Fig.5 Schematic diagram of experimental system
选用煤、红砂岩、花岗岩和大理岩4种试件，尺寸为50 mm×50 mm×100 mm。加载速率为0.3 mm/min，图像采集速率为5帧/s，图像分辨率为1 600像素×1 200 像素。图6、7分别为试件最终破坏形式以及实验过程应力应变曲线。
图6 试件最终破坏形式
Fig.6 Final failure mode of specimen
图7 实验过程应力应变曲线
Fig.7 Stress-strain curves during the experiment
通过数字散斑相关方法对试件标识点时刻散斑图像进行分析，得到图8所示的最大剪应变场云图。从图8可以看出，试件最终都是由一条主裂纹贯通而造成破坏。其中，煤、红砂岩、花岗岩和大理岩的变形局部化带宽度分别为6.37、8.08、7.85和5.25 mm。
图8 最大剪应变场云图
Fig.8 Cloud diagram of maximum shear strain field
对式(51)转换得到煤岩材料内部长度参数计算式为
(53)
将试件材料力学参数以及通过数字图像相关方法分析得到的局部化带宽度代入式(53)，得煤试件、红砂岩试件、花岗岩试件、大理岩试件的材料内部长度为0.95、1.21、1.03、0.62 mm。
4 煤岩变形局部化监测关键指标
从以上的研究发现冲击地压发生和变形局部化是一致的，也可以计算出变形局部化的尺寸。但是否能通过实验室或现场的监测数据来刻画、跟踪变形局部化的过程还需进一步验证。声发射和微震是实验室和现场应用较为广泛的监测技术，采用传感器接收煤岩破裂释放的弹性波，通过理论分析实现对煤岩破裂位置的确定。因此可通过声发射或微震监测等监测数据，引入“空间聚集指标”和“空间尺度显著性指标”，来刻画和跟踪变形局部化过程，进而预测冲击地压的发生。
4.1 监测数据空间聚集性指标
全局Moran’s I是常用的空间自相关指数[30]，具体计算方法如下:
全局Moran’s I为
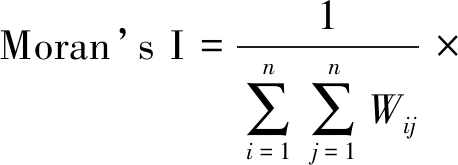
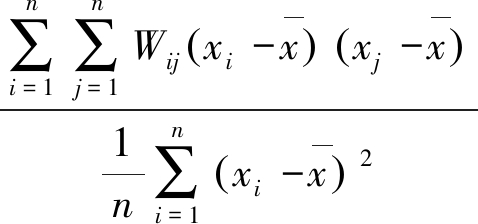
(54)
式中，n为区域单元个数；xi为区域单元i的属性观测值；Wij为空间权重系数，当区域i与j邻接时，Wij=1，当区域区域i与j不邻接时，Wij=0。
当Moran’s I接近1时，为正空间自相关，呈集聚分布；Moran’s I接近-1时，为负空间自相关，呈离散分布；Moran’s I为0时，则无空间自相关，呈随机分布。
Moran’s I的期望值En(I)为
(55)
Moran’s I的方差VARn(I)为
VARn (I)=
(56)
式中，
为第i列和第j列之和。
检验统计量计算：
(57)
根据Z的大小，在设定显著性水平下做出接受或拒绝零假设的判断。双边置信概率α取5%，当Z>1.96，呈集聚格局，当Z<-1.96，呈离散格局。
4.2 监测数据空间尺度显著性指标
空间尺度显著性是一种基于曲面光滑函数的曲面空间分布结构特征统计分析方法，通过二维核函数—局部多变量回归方法进行信号估计、考察各信号点的梯度变化与曲率变化，并进行梯度显著性与曲率显著性分析[31]。
4.2.1 梯度显著性
将观测数据归算到n×m的网格结点上，假设任一结点(i,j)归算后的观测值Yi，j可以表示为
Yi，j=s(i,j)+εi,j
(58)
式中，s为(i,j)点可能存在的信号；εi,j为服从均值为0的正态分布的随机变量，则信号的估计值可由观测数据与核函数的离散卷积表示为
(59)
矩阵形式为
(60)
Kh为高斯密度核函数，公式为
Kh(i，j)=Kh(i)Kh(j)
(61)
对于i=(1-n)…(n-l),j=(l-m)…(m-1)有
(62)
式中，h为核函数带宽，[hmin,hmax]一般为从2倍的最小时间间隔至所研究数据时间段长度的范围内，核函数的带宽对信号估计具有重要影响。
点(i,j)处s的梯度为
G(s)=[(s1)2+(s2)2]1/2
(63)
式中，s1和s2分别为信号曲面s在两正交方向的偏导数。
梯度估计值为
(64)
其中，
两个偏导数是估计值，表示为
(65)
Kh,1(i,j)，Kh,2(i,j)由下式计算得到
(66)
当梯度估计值大于随机噪声水平时，则拒绝假设H0∶G(s)=0，并认为该点在窗宽为h时的尺度空间内具有显著性变化。
该假设检验所依据的基础为假定εi,j服从均值为0的二维正态分布，则信号两方向偏微分估计值服从双变量正态分布：
(67)
可以证明，在上述条件下，
从而
因此，对一些观测点，若
则假设H0被拒绝。这里，概率α′与α的关系为α′=1-(1-α)1/l，分位数
为给定的置信水平，
其中，
为平均有效样本数。
(68)
有效样本数ESS(i,j)：在核函数计算过程中每一个窗口内(带宽为h)包含的样本数目，公式如下：
ESS=(Kh*l)/(Kh(0,0))
(69)
这里l为n×m阶元素为1的矩阵，分母项保证了中心点像素为1，并将其他点的数值进行归算。ESS(i,j)的取值和带宽h成正比关系。
这里以绿色线条表示有显著性变化的梯度线，以粉色线条标注梯度等值线。
4.2.2 曲率显著性
信号在点(i,j)的弯曲属性可由Hessian矩阵表示为
(70)
式中，s11、s22为信号曲面s在两正交方向的二阶偏导数；s12、s21为二阶混合偏导数。
二阶偏导数的估计值为
(71)
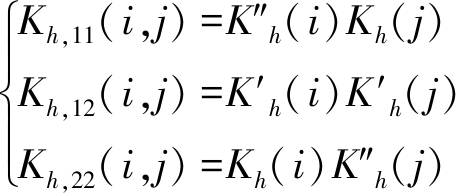
(72)
Hessian矩阵的特征值能够从总体上表示信号曲面的局部弯曲特征。在二维情况下Hessian矩阵特征值可由下式计算：
(73)
当曲面某点的λ+、λ-其中一个或全部计算值大于噪声水平时，则认为该点存在一定的曲率显著性变化。这里用于假设检验的参数为T=max{|λ+|，|λ-|}，其估计值
给定的原假设为H0∶T=0。T的分布较为复杂，但当εi,j服从正态分布(或可用中心极限定理描述)时，T的分布如下三变量正态分布密切相关：
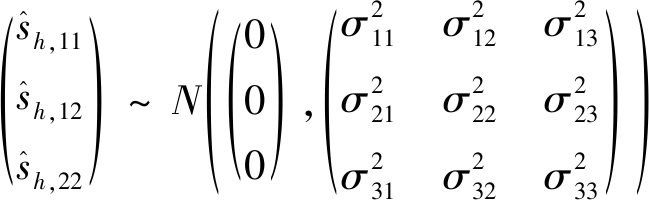
(74)
当给定某置信水平α时，其分位数
可以通过模拟量值的线性插值得到。
所有分析结果以图像的形式给出。若某点接受原假设，则背景色(黑色)不变；拒绝原假设时，通常以不同颜色的圆点标注信号曲面在某点的特征，见表1。
表1 信号曲面特征对照
Table 1 Comparison of signal surface characteristics
颜色信号曲面特征特征值和分位数的关系黄色凹点λ^+,λ^->q^T^橘黄色谷地λ^+>q^T^,λ^-
4.3 监测指标与变形局部化关系
声发射和微震是通过监测岩石变形破坏过程中应变能释放产生的弹性波，反映岩石变形破坏状态。变形局部化本质是微裂纹破坏的聚集过程。
通过声发射和微震的定位，监测微裂纹空间分布，跟踪变形局部化演化。变形局部化演化包括“时间演化”属性和“结构演化”属性2个方面。“时间演化”属性表现为随着载荷作用，岩石变形从初始微裂纹随机扩展向裂纹逐渐向一个条带聚集，图9(a)为岩石变形局部化“时间演化”属性实例[32]。“结构演化”属性表现为变形局部化形成过程中，局部化区域变形存在不均匀性，即局部化区域内部不同位置的微破裂发育存在明显的差异，图9(b)为岩石变形局部化“结构演化”属性实例。
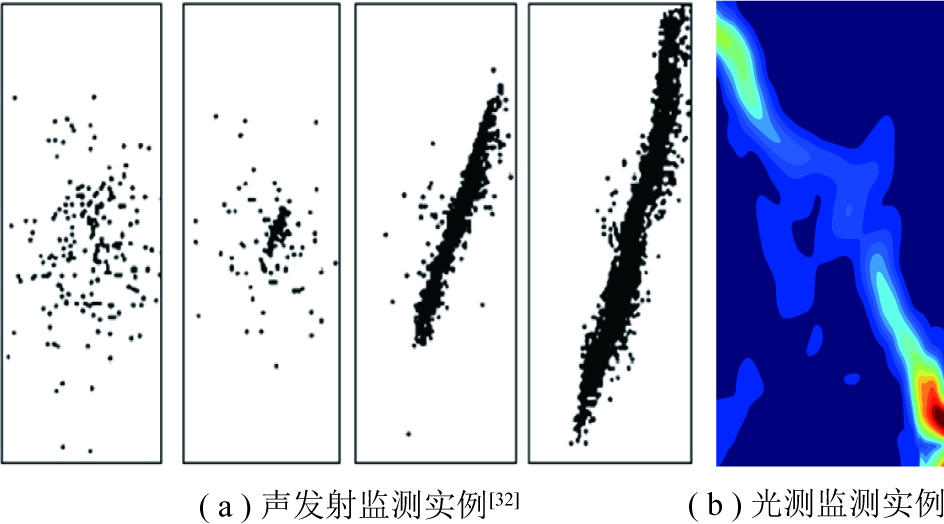
图9 岩石变形局部化“时间演化”和“结构演化”属性
Fig.9 “Time evolution”and “structure evolution”attributes of rock deformation failure localization
监测数据“空间聚集性”指标，可以采用全局Moran’s I，全局Moran’s I能够指示声发射或微震事件空间自相关性，判断随时间变化的声发射或微震事件聚集性，进而分析变形局部化空间分布的“时间演化”属性。
当Moran’s I接近1时，声发射或微震事件呈空间集聚分布，处于变形局部化状态；Moran’s I接近-1时，声发射或微震事件呈空间离散分布；Moran’s I等于0时，声发射或微震事件无空间自相关，呈随机分布。
监测数据“空间尺度显著性”指标，可以采用梯度显著性和曲率显著性，梯度显著性和曲率显著性能够指示声发射或微震信号曲面变化的剧烈程度，进而分析变形局部化空间分布潜在的“结构演化”属性。
梯度显著性包括梯度线和梯度等值线，梯度线显示声发射或微震事件的空间分布密度最大变化方向。梯度等值线显示声发射或微震事件的空间分布密度在某区域变化的剧烈程度。
曲率显著性显示声发射或微震的空间分布密度在某区域变化的复杂程度。信号曲面凹点(黄色)和谷地(橘黄色)表示声发射或微震事件密度较低的地区。信号曲面坡地(紫色)和峰点(蓝色)代表声发射或微震事件空间分布高密度，信号曲面鞍点(红色)总体上围绕信号高密度区域，鞍点包围区域内存在有高密度事件。当信号曲面特征按黄色、橘黄色、红色、紫色和蓝色顺序排列，说明声发射或微震事件空间分布密度曲面变化连续，当各色点的分布秩序较混乱，说明声发射或微震事件的空间分布密度变化剧烈。
根据梯度显著性和曲率显著性从“结构演化”属性角度，分析变形局部化区域内不同位置的微破裂发育情况。
5 实验室和现场冲击地压的预测
5.1 变形局部化预测试件破坏区域
以砂岩和花岗岩试件为例，建立二维平面模型，并进行空间网格划分，取某一时间段声发射数据分析，定位点分布如图10所示。
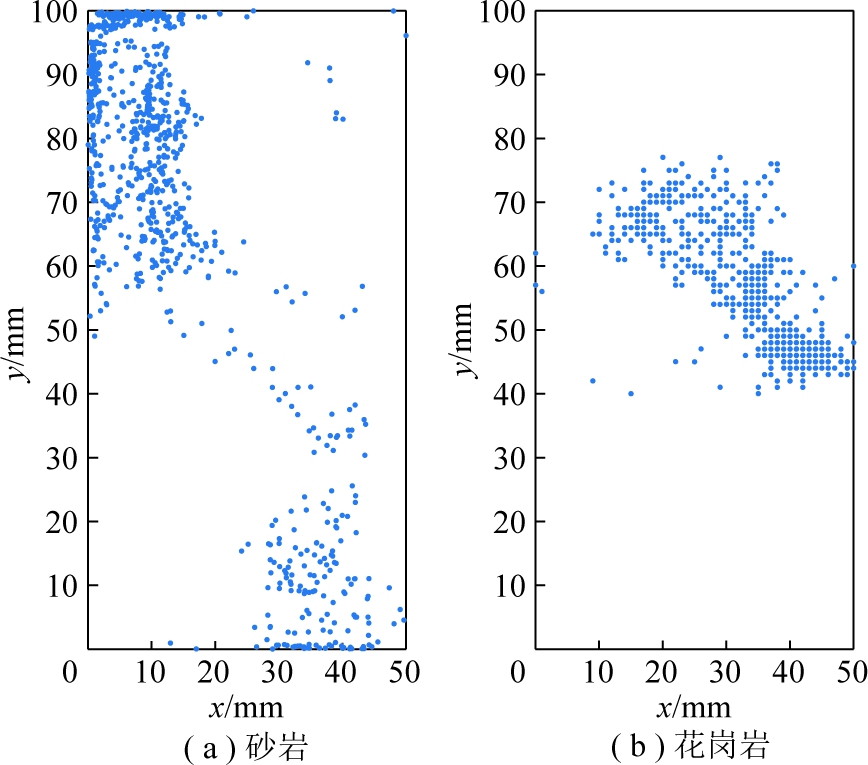
图10 试件声发射二维定位点分布
Fig.10 Two-dimensional localization point distribution of specimen acoustic emission
声发射定位点聚集性可以反映试件变形局部化的“空间”和“数值”特征，计算得出两试件的空间自相关指数见表2。
表2 声发射定位点空间分布Moran’s I及Z
Table 2 Spatial distribution of acoustic emission positioning points Moran’s I and Z
试件事件数Moran’s IE(I)VAR(I)Z砂岩1 0060.651 8-0.010 10.004 99.447 8花岗岩7280.524 1-0.010 10.003 27.724 4
两试件的空间自相关指数随时间的演化如图11所示，由图11可知，随着时间推移，微震事件呈现出明显的聚集性特征。
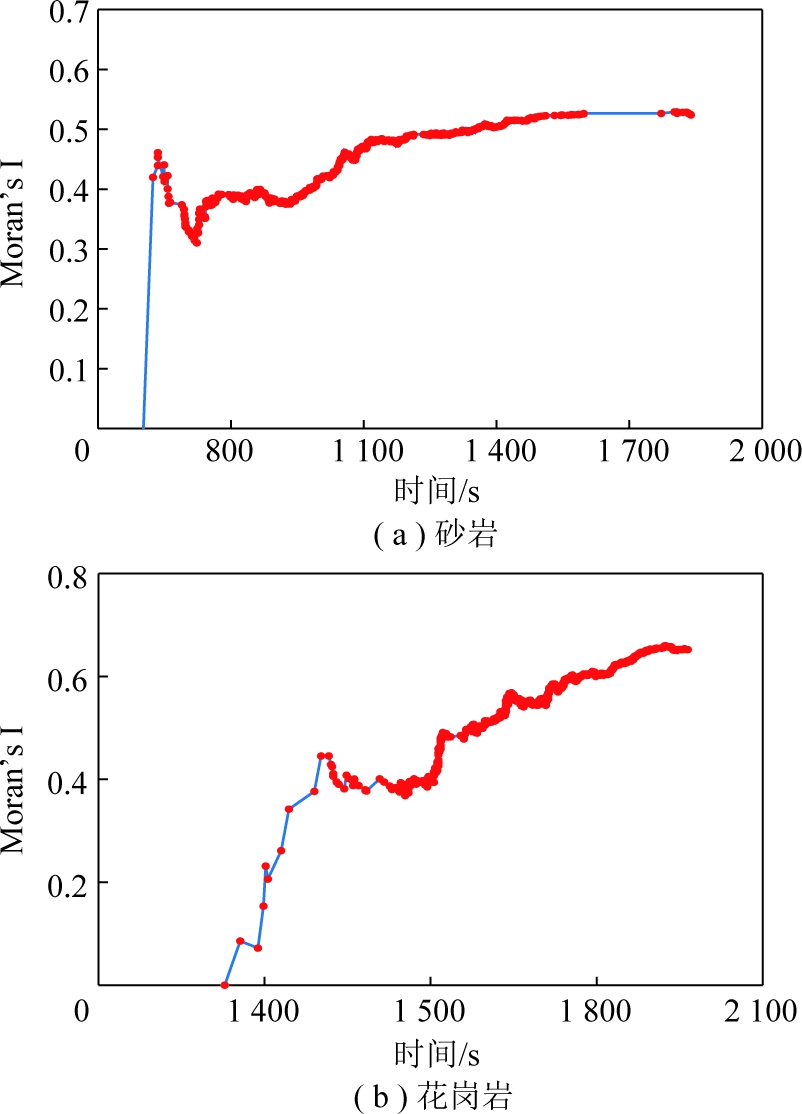
图11 Moran’s I演化曲线
Fig.11 Moran’s I evolution curves
采用上述空间尺度显著性分析方法，区域划分网格为50×100。图12为h=1、α=0.05时计算得到的试件空间分布梯度和曲率显著性结果图。
图12 梯度和曲率显著性
Fig.12 Gradient and curvature significance
由图12(a)可知，梯度等值线较密集于试件左上区域以及右下区域，白色线条框选范围所示，在这两个区域空间内声发射事件分布密度较大，局部化程度较高，由图12(b)可知，左上区域及右下区域由红色和紫色点围绕区域出现峰点(蓝色点)，该局部区域的事件空间分布密度相较仅有橘黄色和黄色点围绕的区域更高，此区域范围内变形局部化程度高于其他区域，预测最终破坏位置将在变形局部化区域发生(如蓝色椭圆线条框选范围所示)。图12(c)为砂岩试件破坏图。
由图12(d)可知，梯度线及梯度等值线主要分布于试件中部区域，白色线条框选范围所示，在此区域内声发射事件空间分布密度较大，局部化程度较高。由图12(e)可知，峰点(蓝色点)主要集中出现在右上区域，均被橘黄色、红色和紫色点围绕，此区域内的事件空间分布密度较大，并且右上区域的峰点数量明显多于左下区域，说明局部化程度相较左下区域更高，预测试件更倾向于此处发生破坏(如蓝色椭圆线条框选范围所示)。图12(f)为花岗岩试件破坏图。
5.2 变形局部化预测冲击地压危险区域
采用工作面掘进期间微震事件数据，通过变形局部化指标分析，预测冲击地压危险区域。
某矿区618综放工作面开采深度1 223.2～1 266 m，工作面可采走向长度650 m，倾向回采水平长度160 m，煤层平均厚度8 m，倾角3°～15°，平均倾角8°。工作面西翼为七采区(未开发)，工作面北翼为井田边界；南翼与回风石门留设保护煤柱80 m(为结束线)；东翼为516综放回采工作面(2018-01-05—2019-02-15)留设平面保护煤柱6 m。618综放工作面相对位置如图13所示。
图13 618综放工作面
Fig.13 618 fully mechanized top-coal caving face
618综放工作面从2021-02-25开始掘进，2022-06-10开始回采。根据618综放工作面掘进期间微震事件定位结果，得出掘进期间的微震事件空间分布如图14所示。
图14 掘进期间微震事件空间分布
Fig.14 spatial distribution of microseismic events during tunneling
微震定位点计算得出的空间自相关指数随工作面掘进过程的演化如图15所示，由图15可知，从618综采工作面掘进开始，微震事件计算的Moran’s I从0不断增大，根据Moran’s I指标意义表明，微震事件从掘进初期的离散分布状态逐渐向聚集状态转变，掘进结束时，工作面微震事件呈现出明显的聚集性特点，即预测工作面变形局部化初步形成。
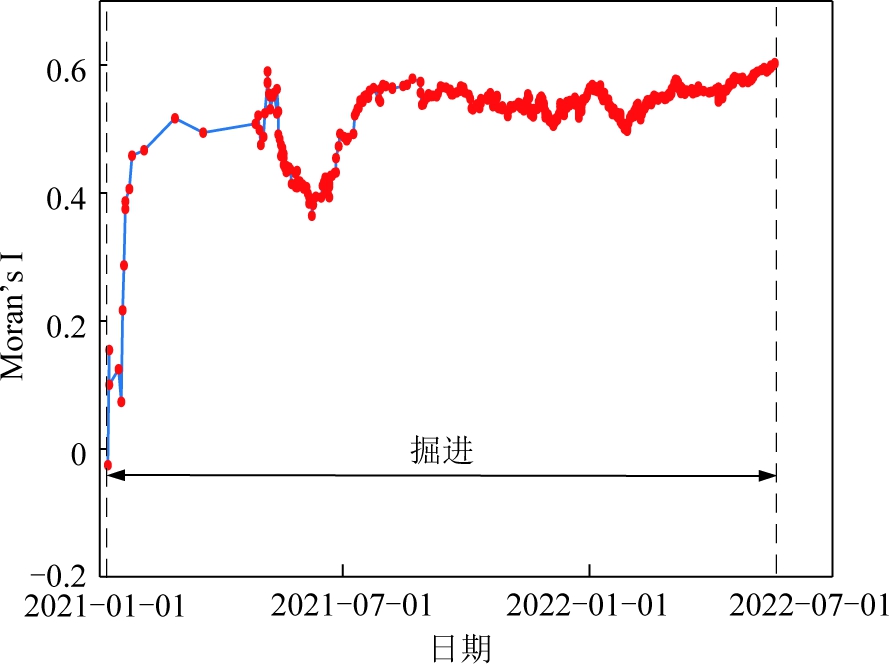
图15 微震事件Moran’s I演化曲线
Fig.15 Moran’s I evolution curve of microseismic event
根据618综放工作面掘进期间微震事件空间分布，计算梯度显著性和曲率显著性指标，预测变形局部化位置。图16为掘进期间微震事件空间分布的梯度显著性和曲率显著性计算结果，区域划分网格为40×100，窗宽h=1，置信水平α=0.05。图16(a)为梯度显著性分析结果，由图16(a)可知，梯度线主要分布于工作面走向的中间区域和工作面终采线区域，采用白色线条框选出梯度等值线密集区，预测框选区域为变形局部化区域。图16(b)为曲率显著性分析结果，采用蓝色椭圆曲线对曲率显著性峰点(蓝色点)进行框选，从“结构演化”属性，预测框选区为冲击地压危险区域。
图16 微震事件空间分布梯度和曲率显著性
Fig.16 Significance of spatial distribution gradient and curvature of microseismic events
工作面从2022-06-10开始回采，图17为回采30 m过程中，微震事件空间分布情况，由图17可知，微震事件主要集中于变形局部化预测区域内，由于受采动应力及其扰动影响，工作面走向中间区域的微震事件明显多于终采线区域，需要采取冲击地压解危技术，防治冲击地压发生。
图17 回采过程中微震事件空间分布
Fig.17 Spatial distribution of microseismic events during mining
6 结 论
(1)建立了冲击地压发生临界条件和变形局部化发生条件，发现冲击地压条件和煤岩变形局部化条件一致，因此提出煤岩变形局部化预测冲击地压的新方法。
(2)采用梯度塑性理论，通过引入内部长度参数，建立变形局部化模型，揭示了煤岩变形破坏向某一区域集中，且集中区具有一定尺度的现象，得到局部化带宽度与材料内部长度、冲击能指数的关系。通过声发射实验监测得到煤岩变形局部化带宽度，并通过对理论公式的间接测量得到煤岩内部长度参数。
(3)提出了刻画、描述和跟踪煤岩变形局部化过程的3个指标，即空间聚集性指标、梯度显著性指标和曲率显著性指标。对实验室煤岩试件的破坏和某矿区工作面冲击地压进行了预测，预测和实际取得了很好的一致性效果，证明本文提出的变形局部化方法预测冲击地压具有可行性。
[1] LIT,CAIMF,CAIM.Are view of mining-inducedin China[J].International Journal of Rock Mechanics and Mining Sciences,2007,44(8):1149-1171.
[2] 钱七虎.岩爆、冲击地压的定义、机制、分类及其定量预测模型[J].岩土力学,2014,35(1):1-6.
QIAN Qihu.Definition,mechanism,classification and quantitative prediction model of rock burst and rock burst[J].Rock and Soil Mechanics,2014,35(1):1-6.
[3] 姜耀东,赵毅鑫.我国煤矿冲击地压的研究现状:机制、预警与控制[J].岩石力学与工程学报,2015,34(11):2188-2204.
JIANG Yaodong，ZHAO Yixin.State of the art：Investigation on mechanism，forecast and control of coal bumps in China[J].Chinese Journal of Rock Mechanics and Engineering，2015，34(11)：2188-2204.
[4] MANSUROVA.Prediction of rock bursts by analysis of induced seismicity data [J].International Journal of Rock Mechanics and Mining Sciences,2001,38(6):893-901.
[5] 宋振骐,卢国志,彭林军,等.煤矿冲击地压事故预测控制及其动力信息系统[J].山东科技大学学报:自然科学版,2006,25(4):1-5.
SONG Zhenqi,LU Guozhi,PENG Linjun,et al.Forecast and control of rockburstincollieries and its dynamic information system[J].Journal of Shandong University of Science and Technology:Natural Science,2006,25(4):1-5.
[6] 姜福兴,苗小虎,王存文,等.构造控制型冲击地压的微地震监测预警研究与实践[J].煤炭学报,2010,35(6):900-904.
JIANG Fuxing，MIAO Xiaohu，WANG Cunwen，et al.Predicting research and practice of tectonic-controlled coal burst by microseismic monitoring[J].Journal of China Coal Society，2010，35(6)：900-903.
[7] 李回贵,高保彬,李化敏.单轴压缩下煤岩宏观破裂结构及声发射特性研究[J].地下空间与工程学报,2015,11(3):612-618.
LI Huigui,GAO Baobin,LI Huamin.Study on macroscopic fracture structure and acoustic emission character of coal rock under uniaxial compression[J].Chinese Journal of Underground Space and Engineering,2015,11(3):612-618.
[8] 肖晓春,丁鑫,潘一山,等.颗粒煤岩破裂过程声发射与电荷感应试验[J].煤炭学报,2015,40(8):1796-1804.
XIAO Xiaochun,DING Xin,PAN Yishan,et al.Experiment of acoustic emission and charge induction in granular coal rock failure[J].Journal of China Coal Society,2015，40(8):1796-1804.
[9] 窦林名,牟宗龙,李振雷,等.煤矿冲击矿压监测预警与防治研究进展[J].煤矿支护,2015(2):17-26.
DOU Linming,MOU Zonglong,LI Zhenlei,et al.Research progress on monitoring,warning and prevention of coal mine impact pressure[J].Coal Mine Support,2015(2):17-26.
[10] 刘善军,魏嘉磊,黄建伟,等.岩石加载过程中红外辐射温度场演化的定量分析方法[J].岩石力学与工程学报,2015,34(S1):2968-2976.
LIU Shanjun,WEI Jialei,HUANG Jianwei,et al.Quantitative analysis methods of infrared radiation temperature field variation in rock loading process[J].Chinese Journal of Rock Mechanics and Engineering,2015,34(S1):2968-2976.
[11] 曹安业,井广成,窦林名,等.不同加载速率下岩样损伤演化的声发射特征研究[J].采矿与安全工程学报,2015,32(6):923-928.
CAO Anye,JING Guangcheng,DOU Linming,et al.Damage evolution law based on acoustic emission of sandy mudstone under different uniaxial loading rate [J].Journal of Mining &Safety Engineering,2015,32(6):923-928.
[12] 李宏艳,康立军,徐子杰,等.不同冲击倾向煤体失稳破坏声发射先兆信息分析[J].煤炭学报,2014,39(2):384-388.
LI Hongyan,KANG Lijun,XU Zijie,et al.Precursor information analysis on acoustic emission of coal with different outburst proneness [J].Journal of China Coal Society,2014,39(2):384-388.
[13] 吕玉凯,蒋聪,成果,等.不同冲击倾向煤样表面温度场与变形场演化特征[J].煤炭学报,2014,39(2):273-279.
LÜ Yukai,JIANG Cong,GENG Guo,et al.Evolution of the surface temperature field and deformation field of different impact proneness coal specimens [J].Journal of China Coal Society,2014,39(2):273-279.
[14] 王春秋,蒋邦友,顾士坦,等.孤岛综放面冲击地压前兆信息识别及多参数预警研究[J].岩土力学,2014,35(12):3523-3530.
WANG Chunqiu,JIANG Bangyou,GU Shitan,et al.Study of precursor information recognition and multiparameter early warning before rockburst of island fully mechanized caving face [J].Rock and Soil Mechanics,2014,35(12):3523-3530.
[15] 宋义敏,杨小彬.煤破坏过程中的温度演化特征实验研究[J].岩石力学与工程学报,2013,32(7):1344-1349.
SONG Yimin,YANG Xiaobin.Experimental study of temperature evolution characteristics during deformation and destruction process of coal [J].Chinese Journal of Rock Mechanics and Engineering,2013,32(7):1344-1349.
[16] 姜福兴,XUN Luo,杨淑华.采场覆岩空间破裂与采动应力场的微震探测研究[J].岩土工程学报,2003,25(1):23-25.
JIANG Fuxing,XUN Luo,YANG Shuhua.Study on microseismic monitoring for spatial structure of overlying strataand mining pressure field in longwall face [J].Chinese Journal of Geotechnical Engineering,2003,25(1):23-25.
[17] 赵毅鑫,姜耀东,王涛.“两硬”条件下冲击地压微震信号特征及前兆识别[J].煤炭学报,2012,37(12):1960-1966.
ZHAO Yixin,JIANG Yaodong,WANG Tao.Features of microseismic events and precursors of rock burst in underground coal mining with hard roof [J].Journal of China Coal Society,2012,37(12):1960-1966.
[18] 赵阳升.岩体力学发展的一些回顾与若干未解之百年问题[J].岩石力学与工程学报,2021,40(7):1297-1336.
ZHAO Yangsheng.Retrospection on the development of rock mass mechanics and the summary of some unsolved centennial problems[J].Chinese Journal of Rock Mechanics and Engineering,2021,40(7):1297-1336.
[19] 潘一山，唐治，李忠华，等.不同加载速率下煤岩单轴压缩电荷感应规律研究[J].地球物理学报，2013，56(3)：1043-1048.
PAN Yishan，TANG Zhi，LI Zhonghua，et al.Research on the charge inducing regularity of coal rock at different loading rate in uniaxial compression tests[J].Acta Geophysica Sinica，2013，56(3)：1043-1048.
[20] 潘一山,宋义敏.岩石变形破坏局部化的理论与实验研究[C]//中国岩石力学与工程学会第六次学术大会论文集.2000:260-264.
[21] 郑捷,姚孝新,陈顒.岩石变形局部化的实验研究[J].地球物理学报,1983,26(6):554-563.
ZHENG Jie,YAO Xiaoxin,CHEN Yong.An experimental study on localization of deformation of rock[J].Acta Geophysica Sinica,1983,26(6):554-563.
[22] 潘一山,杨小彬,马少鹏.岩石变形破坏局部化的白光数字散斑相关方法研究[J].岩土工程学报,2002，24(1):98-100.
PAN Yishan,YANG Xiaobin,MA Shaopeng.Study on deformation failure localization of rock by white light digital speckle correlation method[J].Chinese Journal of Geotechnical Engineering,2002，24(1):98-100.
[23] 马少鹏,周辉.岩石破坏过程中试件表面应变场演化特征研究[J].岩石力学与工程学报,2008,27(8):1667-1673.
MA Shaopeng,ZHOU Hui.Surface strain field evolution of rock specimen during failure process[J].Chinese Journal of Rock Mechanics and Engineering,2008,27(8):1667-1673.
[24] 宋义敏,邢同振,赵同彬,等.岩石单轴压缩变形场演化的声发射特征研究[J].岩石力学与工程学报,2017,36(3):534-542.
SONG Yimin,XING Tongzhen,ZHAO Tongbin,et al.Acoustic emission characteristics of deformation field development of rock under uniaxial loading[J].Chinese Journal of Rock Mechanics and Engineering,2017,36(3):534-542.
[25] LINKOV A M.Rockbursts and the instability of rock masses[J].International Journal of Rock Mechanics &Mining Sciences &Geomechanics Abstracts,1996,33(7):727-732.
[26] 章梦涛.冲击地压机理的探讨[J].阜新矿业学院学报,1985(S1):65-72.
ZHANG Mengtao.Disscussion on the mechanism of coal burst[J].Journal of Fuxin Mining Institute,1985(S1):65-72.
[27] 潘一山.冲击地压发生和破坏过程研究[D].北京：清华大学,1999.
PAN Yishan.Study on rockburst initiation and failure propagation [D].Beijing:Tsinghua University,1999.
[28] 齐庆新,史元伟,刘天泉.冲击地压粘滑失稳机理的实验研究[J].煤炭学报,1997,22(2):144-148.
QI Qingxin,SHI Yuanwei,LIU Tianquan.Mechanism of instability caused by viscous sliding in rockburst[J].Journal of China Coal Society,1997,22(2):144-148.
[29] 高明仕,窦林名,张农,等.煤(矿)柱失稳冲击破坏的突变模型及其应用[J].中国矿业大学学报,2005,34(4):433-437.
GAO Mingshi,DOU Linming,ZHANG Nong,et al.Cusp catastrophic model for instability of coal pillar burst damage and analysis of its application[J].Journal of China University of Mining &Technology,2005,34(4):433-437.
[30] 陈彦光.基于 Moran 统计量的空间自相关理论发展和方法改进[J].地理研究,2009,28(6):1449-1463.
CHEN Yanguan.Reconstructing the mathematical process of spatial auto correlation based on Moran’s statistics[J].Geographical research,2009,28(6):1449-1463.
[31] 陈时军.不同构造环境的地震活动丛集特征研究[D].北京：中国地展局地质研究所,2004.
CHEN Shijun.Clustering characteristics of spatial-temporal distribution of earthquakes in different tectonic regions[D].Beijing：Institute of Geology,China Earthquake Administration,2004.
[32] 耶格 J C,库克 N G W.岩石力学基础[M].中国科学院工程力学研究所译.北京：科学出版社,1981:576-626.
