煤矿采场顶板破坏及采场上覆岩层垮落过程一直是采矿界关心的重要问题,有许多工程设计方法和理论[1-5]描述了岩层破断特征及工作面顶板矿压控制方法,这些方法主要针对岩层特点建立数学模型,并采用材料力学和结构力学的计算方式,对实际情况进行了简化处理。为了更充分的模拟实际情况,采用各类数值方法模拟地下施工过程已得到普遍应用,主要可以分为非连续方法和连续性方法两个大类;非连续方法中应用较多的是离散元方法[6-8],连续方法包括常规有限元方法[9-11]、损伤分析方法[12-13]、扩展有限元方法[14]等。
非连续方法能够较好的体现大变形、破坏的情况,但离散元方法的参数确定及块体的预先划分方式对计算结果影响较大,计算难度高;连续性方法中,以损伤力学为基础的数值方法通常所需参数较多,损伤局部化计算复杂,有时需要考虑动态演化过程;扩展有限元方法避免了复杂的网格重构,但其计算精度受对待求问题特征了解程度的影响[15],在工程实践中通常难以应用。有限元方法较为常用,但其变形协调假定在根本上排除了变形不协调存在的情况,进而无法直接反映开裂、破坏问题。因此在连续体中想要研究开裂破坏情况,不能忽视变形不协调的影响,如关键层理论[2]就将层间变形不协调作为关键层位的判据之一。现有的开采过程有限元模拟主要基于单应力或单应变破坏准则或是否达到屈服面作为结构破坏部位的判定方式,仍然依赖于在变形协调条件下计算有解的情况,对于变形不协调的影响体现不足。因此,在有限元方法及连续性假设的基础上,找到能够反映结构应力调整过程、指示连续介质中的变形不协调部位的数值方法,是本文关注的主要问题。
笔者从连续介质力学的基本定义出发,将结构的变形不协调问题转换为连续介质力学分析解的存在性问题[16]:在静态或准静态连续介质边值问题分析过程中,要求结构同时满足平衡条件、变形协调条件及本构关系;若有解,则结构总体能够保持连续性,结构变形协调;若解不存在,则结构无法保持变形协调,存在变形不协调部位,并表现为损伤、开裂的破坏形式。具体到有限元方法中,变形加固理论[17]认为,非线性弹塑性有限元解不存在时,作用力对应的平衡应力场超出屈服面,此时作用力和抗力的差值称为不平衡力,若在对应位置施加与不平衡力等大且反向的加固力,则结构可以保持平衡,若不施加加固力则结构破坏,通过不平衡力分布定量确定变形不协调位置及产生变形不协调的可能性。
笔者采用自主开发的数值计算程序TFine进行同忻煤矿8102工作面开采过程中的坚硬顶板破坏过程数值模拟。TFine早期主要用于常规弹塑性有限元模拟计算,杨强等[16-19]提出变形加固理论及非平衡弹塑性力学理论后使用该软件计算结构不平衡力。在过去的研究中,不平衡力多用于指示与不平衡力等大且反向的全局最优加固力,以便对坝基、边坡坡脚等位置进行高效率加固,使结构稳定。而笔者从连续介质力学的基本定义出发,对不平衡力的理论基础进行了重新梳理,认为其可以指示破坏区域,并以层间关键部位重设网格模拟变形不协调对不平衡力发展的影响,最终实现坚硬顶板破断发展过程模拟,为顶板控制来压分析、水力压裂层位选择等方面提供数据支撑。
1 工作面基本地质条件
山西省同忻煤矿8102工作面为同忻煤矿一盘区东翼最后一个未开采的孤岛工作面,其两侧工作面(8101工作面、8103工作面)均已采空,且工作面上部为侏罗系煤层采空区。8102工作面倾向宽度251 m,走向长度1 399 m,煤层平均厚度16.7 m,顶板岩层存在多层厚硬岩层,采用综合机械化放顶煤开采。8103工作面回采过程中,其基本顶及上覆坚硬岩层的垮落步距大,矿压显现剧烈,强矿压导致的动力现象严重,因此有必要对8102孤岛工作面进行数值模拟,研究坚硬顶板破断过程。
根据8102工作面上的1602井层位,在合理合并过薄的岩层后,得到8102工作面3-5煤层和其上部的40层岩层(总高度为290.7 m)层位及厚度详细关系见表1;距离煤层超过290.7 m直至地面的岩层概化为上覆岩层。
表1 岩层厚度及性质
Table 1 Rock strata thickness and property

编号厚度/m岩层编号厚度/m岩层43184.30上覆岩层223.60细砂岩4211.60粉砂岩213.40粉砂岩417.80中砂岩204.90细砂岩403.80粉砂岩1920.25粉砂岩3923.90细砂岩186.65粗砂岩383.60粉砂岩177.20粉砂岩3716.25细砂岩165.05泥岩364.95粉砂岩155.40中砂岩356.60煤层144.15细砂岩345.20粉砂岩1316.05粗砂岩333.40中砂岩124.15细砂岩324.10细砂岩113.20泥岩316.75粉砂岩104.00粗砂岩309.95细砂岩92.90细砂岩297.50粉砂岩84.07泥岩285.60细砂岩73.79粉砂岩272.50粗砂岩65.51粗砂岩266.60细砂岩57.58细砂岩252.60中砂岩410.90粗砂岩245.25细砂岩32.77炭质泥岩238.35粉砂岩218.883-5煤125.00底板
现场采取岩样,在实验室进行单轴压裂试验、巴西劈裂试验,试验结果见表2。岩石内摩擦因数f及黏聚力c可通过摩尔库伦准则,由单轴抗压强度及抗拉强度求得。
表2 岩石性质参数
Table 2 Mechanical parameters of the rock

岩层密度/(g·cm-3)弹性模量/GPa单轴抗压强度/MPa抗拉强度/MPa细砂岩2.3711.299.773.17中砂岩2.514.6455.783.01粗砂岩2.223.7343.381.93炭质泥岩2.305.9358.921.78粉砂岩2.257.8659.201.16煤样1.591.3210.710.21
2 数值方法概述
2.1 连续介质边值问题
静态或准静态连续介质力学边值问题是给定体积力、应力边界条件和位移边界条件,求解结构应力应变状态的问题。结构要求同时满足以下3个条件:平衡条件、变形协调条件及本构关系。其中,平衡条件包括平衡微分方程及应力边界条件,为
(1)
其中,σij为结构应力场;fi为体力在体积上的分布;V为体积;Ti为边界面力;nj为边界外法线方向;Sσ为应力边界。变形协调条件包括几何方程和位移边界条件,为
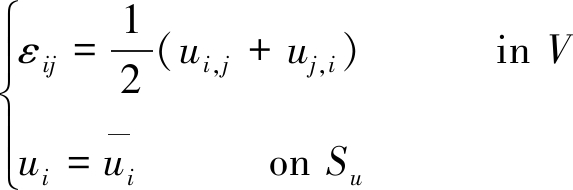
(2)
其中,εij为结构应变;u为位移;![]() 为边界位移;Su为位移边界。根据式(1),可求出满足平衡要求的应力场;根据式(2),可根据边界条件得到位移场,再由几何方程微分得到应变场;最终由本构关系得到应力与应变之间的联系。此时结构能够满足平衡条件、变形协调条件及本构关系的要求。
为边界位移;Su为位移边界。根据式(1),可求出满足平衡要求的应力场;根据式(2),可根据边界条件得到位移场,再由几何方程微分得到应变场;最终由本构关系得到应力与应变之间的联系。此时结构能够满足平衡条件、变形协调条件及本构关系的要求。
对于弹性模型,由于其本构关系对材料承载能力没有特定限制,总能求解出满足上述要求的应力应变结果,通常通过额外的应力或应变破坏准则来判断材料变形不协调情况。而对于弹塑性模型,本构关系除了反映应力应变关系外,还包含了屈服面的要求,使求解过程受到了新的限制。求解出一组满足平衡条件及变形协调条件的应力应变状态后,需要检查其是否满足材料屈服条件,并通过迭代计算消除应力状态超出屈服面的部位。在始终满足平衡条件、变形协调条件和应力应变关系的前提下,若结构应力最终能够全部处于屈服面内,此时弹塑性计算有解,系统是一个自平衡应力场,通常不会产生大的位移。若弹塑性计算迭代后最终无法回到屈服面内,则意味着在给定条件下无法找到同时满足平衡条件、变形协调条件及本构关系的解,即意味着无法同时满足这3条基本要求,结构无法保持变形协调状态。
文献[16]对弹塑性解不存在的情况进行了讨论,认为弹塑性迭代过程实质上是寻找一个能够满足结构变形协调要求的解,应力状态在屈服面上的结构塑性区并不能直接视为破坏,而弹塑性计算无解时结构才真正无法保持变形协调,在应力状态超出屈服面的部位应出现变形不协调,并通过损伤、开裂的形式体现;且应力状态偏离屈服面越多,变形不协调导致的破坏可能性越大;从而从连续介质力学求解的基本定义出发,描述了材料变形不协调的判定方式,提出了新的数值模拟思路。
由上述论证可知,想要定量描述变形不协调程度,需要考虑最终应力状态超出屈服面后材料的行为模式,而经典的弹塑性理论要求最终应力处于屈服面内,需要引入黏塑性方法对屈服面外应力的发展规律进行求解。
2.2 黏弹塑性本构关系及不平衡力计算
2.2.1 黏塑性本构关系的弹塑性近似
以下参考黏塑性模型的对超出屈服面的应力的处理方法,对经典弹塑性模型进行拓展,关注弹塑性计算迭代后无法消除的屈服面外应力情况,并阐明其物理意义。过应力黏塑性Duvaut-Lions模型中与超出屈服面的应力σ1相关的等式[20]为
(3)
其中,![]() 为黏塑性应变率;τ为黏滞系数;C为柔度张量;σ为屈服应力,由满足平衡条件的实际应力状态σ1通过最近点投影法确定,要求σ1在屈服面外,σ在屈服面上。Duvaut-Lions模型采用最近点投影法[21]确定屈服面上的应力σ,实质上包含了最小塑性余能原理[22]:在黏塑性计算的每一时刻,结构的过应力场Δσvp=σ1-σ都趋向于使结构塑性余能ΔE最小。其中,结构塑性余能ΔE为过应力Δσvp=σ1-σ的范数在结构体积上的的积分:
为黏塑性应变率;τ为黏滞系数;C为柔度张量;σ为屈服应力,由满足平衡条件的实际应力状态σ1通过最近点投影法确定,要求σ1在屈服面外,σ在屈服面上。Duvaut-Lions模型采用最近点投影法[21]确定屈服面上的应力σ,实质上包含了最小塑性余能原理[22]:在黏塑性计算的每一时刻,结构的过应力场Δσvp=σ1-σ都趋向于使结构塑性余能ΔE最小。其中,结构塑性余能ΔE为过应力Δσvp=σ1-σ的范数在结构体积上的的积分:
(4)
假设初始条件、边界条件均一致,ZIENKIEWICZ等[23]认为对Δt足够小的瞬态过程,黏塑性与弹塑性结果的差异是可以接受的;CHABOCHE[24]证明了单一材料弹塑性计算结果是黏塑性时间趋于无穷大的极限形式。弹塑性模型与黏塑性模型具有接近的物理意义,为弹塑性模型引入该屈服面外应力处理方法提供了理论基础。对于弹塑性模型,本文同样采用最近点投影法进行弹塑性迭代。YANG 等[22]、冷旷代[25]推导出,弹塑性计算采用最近点投影法进行迭代时,弹塑性模型求解应变增量时的公式如下所示,与Duvaut-Lions黏塑性模型在形式上相似:
Δεp=C:(σ1-σ)
(5)
其中,σ由满足平衡条件的应力状态σ1通过最近点投影法确定。由于此处的弹塑性迭代同样采用了最近点投影法,且式(5)与式(3)具有近似的形式,有理由相信,超出屈服面的弹塑性迭代过程同样是使结构塑性余能趋于最小值的过程,即塑性应力Δσp=σ1-σ也应使结构塑性余能ΔE最小,此时的结构塑性余能ΔE对应为弹塑性计算中超出屈服面的塑性应力Δσp的范数在结构体积上的的积分:
(6)
2.2.2 基于最小塑性余能原理计算不平衡力
在规定弹塑性迭代采用最近点投影法,并引入最小塑性余能原理后,经典弹塑性计算得到拓展,以最小塑性余能原理对平衡应力处于屈服面外的情况做出了约束,使得最终的Δσp可以通过式(6)的变分计算得出,从而使弹塑性模型能够处理平衡应力场最终位于屈服面外的情况。同时,笔者获得了一个重要物理量:弹塑性迭代得到的屈服面外塑性应力Δσp=σ1-σ,将其称为不平衡应力场。
在实际有限元数值计算中,本文考虑理想弹塑性材料,屈服条件保持不变,采用D-P准则作为屈服条件。σ1为满足平衡条件的应力场,σ为满足屈服条件的实际应力场。若σ1处处满足屈服条件f(σ1)≤0则结构保持稳定,退化为经典平衡态弹塑性分析;若存在区域使f(σ1)>0,则迭代计算寻找满足最小塑性余能原理的Δσp、σ1、σ,其中Δσp为不平衡应力场,调整迭代过程如图1所示。

图1 弹塑性应力调整
Fig.1 Iteration of elasto-plastic stress
为了更加直观的反映塑性变形驱动力的分布,将不平衡应力场Δσp的等效节点力定义为不平衡力Q,则有
F-P
(7)
式中,B为刚度矩阵;e为对所有单元求和。
σ1为满足平衡条件的应力场,F为外荷载的等效节点力,满足:
(8)
式中,σ为满足屈服条件的应力场;P为结构自承力,满足:
(9)
理想弹塑性模型中的最小塑性余能原理也可以表述为:在给定超出结构极限承载能力的外荷载时,实际结构的自承能力最大而不平衡力最小。
根据上述计算过程,笔者将弹塑性迭代得到的屈服面外应力Δσp=σ1-σ定义为不平衡应力场,并将不平衡应力场在有限元数值计算中的等效节点力称为不平衡力Q,若迭代最终存在无法消除的不平衡力Q,则意味着在对应位置的弹塑性连续体计算无法达到平衡,现实结构将以变形不协调的形式进行调整,体现为结构开裂、破坏等形式。
2.3 不平衡力的物理意义
由2.1及2.2节的计算及推导,笔者得到了重要的物理量:不平衡应力场Δσp及其等效节点力不平衡力Q。不平衡力是对弹塑性计算进行扩展后的产物,其有两重物理含义:
(1)由不平衡力的计算过程可知,不平衡应力场及不平衡力直接指示了弹塑性计算无法收敛时应力状态超出屈服面的具体程度。不平衡力越大,意味着应力状态偏离屈服面越多;不平衡力为0时,不存在应力超出屈服面的部位,计算退化为经典弹塑性分析解。以上即为不平衡力的直接定义。
(2)由连续介质力学的基本方程可知,出现不平衡力的位置意味着结构变形协调条件在该处无法满足。若迭代最终存在无法消除的不平衡应力场Δσp及不平衡力Q,意味着在结构变形协调条件强制满足的要求下,无法找到一组应力应变使得计算有解,真实世界中的结构只能通过在不平衡应力场出现处产生损伤、开裂等变形不协调情况来消除不平衡力的影响,最终趋向平衡状态。因此,不平衡应力场Δσp及不平衡力Q实质上是一种材料变形不协调可能性的表述,可用于指示材料出现变形不协调的可能性,指示材料出现开裂、破坏的可能性及范围。
因此,将不平衡力分布区作为判定开裂、破坏的指示物理量,应用于煤炭开采的数值模拟过程中,从而判定开采过程中岩层产生开裂、破坏的影响范围,从这个角度来看,不平衡力分布区所指示的范围与垮落带、裂隙带比较接近。
相较于传统有限元方法采用应力准则、应变准则或屈服区判定开裂的方法,该方法指出了出现变形不协调的根本原因是无法满足连续介质力学的基本假设,体现了弹塑性模型中屈服面的整体影响,在保持有限元方法计算效率高、收敛性强、网格依赖性较低的情况下,指示出现非连续性的具体部位,为结构的开裂破坏部位判断提供依据。
以不平衡力作为变形不协调的表征方法在水力压裂[26]及拱坝坝基分析[27]等领域已有实际应用。变形加固理论[16-19]对不平衡力及相关数值方法进行了详细论述。
2.4 开采过程坚硬顶板破坏及岩层扰动模拟
2.4.1 层间变形不协调对岩层扰动的影响
由工程实践经验及研究可知,开采产生的影响可以传递到相对高位的岩层,高位坚硬顶板同样会对采场矿压产生影响[28-29],由于过强的连续性假定,传统的弹塑性有限元方法所得的屈服区主要集中在直接顶及附近的低位岩层,难以真实体现开采产生的扰动对岩层的影响范围。在实际开采过程中,岩层及层间的连续性受到严重破坏,岩层变形后通常出现互相分离的情况,模型试验结果如图2所示。在有限元模型的计算中,这种程度的大变形及离散情况需要采用特定计算方式进行模拟。

图2 相似模型试验中的离层现象
Fig.2 Abscission layer in similar model test
考虑岩层破断过程主要在竖直方向上传递,且层与层之间的界面相对连续性较弱,大规模的变形不协调在层间发生的可能性高,竖直方向上的位移扰动也较大。常用的分析理论如关键层理论[2]同样强调层间的变形协调关系,以此作为关键层的判据之一。因此,在采用基于不平衡力的有限元数值模拟方法的同时,同样要特别关注层与层之间变形不协调的情况。
2.4.2 考虑层间变形不协调的数值模拟方法
试算结果表明,开采过程中不平衡力首先会自然集中在层间,如图3(a)所示,符合层间易发生变形不协调的实际情况。因此,笔者在不平衡力对变形不协调区域的指示作用的基础上,采取重设网格的方式体现层间变形不协调对整体结构不平衡力发展的影响。对于给定的开采距离,不平衡力分布范围的计算步骤如下:
(1)开采至该给定距离时,首先进行初步计算,获得不平衡力分布区域如图3(a)所示。
(2)寻找计算结果中岩层间的不平衡力集中区域,并移除岩层间不平衡力聚集区对应的薄层单元,如图3(b)所示。由2.1~2.3节分析可知,若两岩层之间不平衡力聚集,则说明此处连续性被破坏,出现变形不协调情况及离层现象,此时通过移除层间薄层单元来完全破坏层与层之间的连续性,以模拟离层情况,反映开采对岩层造成的扰动向上传播的过程。

图3 离层模拟方法
Fig.3 Simulation of abscission layer
(3)对移除薄层单元后的模型再次进行计算,获得新的不平衡力区域。薄层单元移除模拟了发生离层后的岩层受力情况,其对应的岩层下部悬空,受力条件恶化,不平衡力将向上继续发展。
(4)重复步骤(2)、(3)的计算过程,直至不平衡力不再发展,意味着此时为最终的不平衡力分布区域,一个典型的发展过程如图4所示。此时的不平衡力分布区域,即为最终受开采扰动导致岩层破坏、变形的范围。

图4 考虑离层情况的不平衡力发展过程
Fig.4 Development of unbalanced force in the case of separation layer
三维非线性有限元程序TFine软件可用于计算不平衡力。对其进行二次开发,并实现上述步骤(1)~(4)计算流程,包括层间薄层单元不平衡力聚集区的判定、移除及重新计算,可得到任意开采距离下不平衡力分布区域,即开采扰动导致岩层破坏、变形的范围。设置不同开采距离,并按照上述方法进行计算,即可得出煤矿开采全过程中的不平衡力分布区域变化,并依此进行坚硬顶板破坏及岩层扰动情况的分析。
常规弹塑性有限元方法与本文计算结果对比如图5所示。由于过强的连续性,弹塑性有限元所得的屈服区主要集中在直接顶及附近的低位岩层,难以体现开采产生的扰动情况。而采用不平衡力、考虑离层情况的计算方法在保持有限元计算优点同时,可更为准确的反映开采对岩层的扰动影响范围。

图5 屈服区与不平衡力分布区对比
Fig.5 Comparison between yield zone and distribution of unbalanced force
3 数值计算及验证
3.1 数值模型及计算工况
将该数值方法应用至同忻煤矿8102工作面数值模拟,根据表1的层位厚度关系、表2的岩石力学参数进行建模。为了避免煤层过于接近模型底部约束,设置25 m厚的底板以消除底部约束的影响;煤层上方超过270 m位置的更高处岩层对煤层开采的影响不大,故合并为统一材料的上覆岩层,体现地应力作用。其中,编号为35的侏罗系煤层在先前的开采中已经采空,在此模拟中以软化模量的形式进行体现。
建立8102工作面三维有限元弹塑性地质模型,如图6所示。此三维模型模拟了煤层及上部40层实际岩层的情况,长宽高分别为1 683、600、500 m,单元数量为158 760,节点数量为187 579。两侧已采空的8101及8103工作面采用调整模量的方式体现。

图6 三维数值模型示意
Fig.6 Schematic of the 3D numerical model
为了实现2.4节中的离层模拟方法、充分体现层间变形不协调的影响,模型的任意两岩层交界处均设置了2 cm厚度的薄层单元,其物理性质与薄层单元上部岩层保持一致,以便后续移除(图7)。模型采用以摩尔库伦准则顶点拟合外接圆的D-P屈服准则进行弹塑性计算。

图7 模型XOZ剖面示意(平行于开采方向)
Fig.7 Schematic of model XOZ profile (Parallel to mining direction)
3.2 坚硬顶板断裂与上覆岩层破坏规律分析
以10 m为步长,分别计算了8102工作面开采10~300 m不同距离时的不平衡力分布情况,以8102工作面中部截面作为云图取值截面,计算结果如图8所示。

图8 开采150 m不平衡力分布
Fig.8 Distribution of unbalanced force in the mining process of 150 m
以下对开采过程中能够体现岩层破断规律及厚硬顶板控制效果的不平衡力发展典型过程进行详细说明,如图9、10所示。
(1)在开采10~70 m的前期,不平衡力随开采范围的增加稳步向上层蔓延,意味着顶板垮落范围随开采距离逐渐增大,不平衡力分布范围没有突增或者迟缓的情况,此时变形不协调区域的范围不受特定顶板的控制,主要取决于开采范围。
(2)开采80~100 m的过程如图9(a)~(c)所示,不平衡力范围在水平方向上保持蔓延,但在向上延伸过程受阻,煤层上方48.87 m处的13号岩层(以下称为厚硬岩层1)阻止了岩层破坏范围向上延伸,其下方岩层破坏,出现离层现象,而上部岩层连续性保持完好,意味着厚硬岩层1承担了其上部地层的应力,且其下没有可供承载的地层。
(3)在开采110 m时,如图9(d)所示,不平衡力聚集区突破厚硬岩层1,到达厚硬岩层1上方的岩层中。在此之后至开采到200 m的过程中,不平衡力发展趋势与开采10~70 m的过程类似,不平衡力分布范围随开采距离逐渐增大。

图9 80~110 m开采长度不平衡力分布
Fig.9 Distribution of unbalanced force during the mining process of 80-110 m
(4)开采200~260 m的过程如图10(a)~(c)所示,再次出现不平衡力范围在水平方向上保持蔓延,而在向上延伸过程受阻的情况,煤层上方93.37 m处的19号岩层(以下称为厚硬岩层2)阻止了岩层破坏范围向上延伸,其下方岩层破坏,出现离层现象,而上部岩层连续性保持完好,意味着厚硬岩层2同样承担了其上部地层的应力,且其下没有可供承载的地层。
(5)在开采270 m时,如图10(d)所示,不平衡力聚集区突破厚硬岩层2,到达厚硬岩层2上方。在此之后的开采过程中不平衡力发展趋势与开采10~70 m的过程类似,不平衡力分布范围随开采距离逐渐增大。

图10 200~270 m开采长度不平衡力分布
Fig.10 Distribution of unbalanced force during the mining process of 200-270 m
根据以上分析可知:
(1)不平衡力分布范围主要受开采长度影响,通常情况下不平衡力分布范围和开采长度直接相关,但其分布高度同时会受到坚硬顶板的影响。
(2)在开采80~100 m和开采200~260 m的过程中,分别对应的厚硬层位下部不平衡力较大,在不平衡力分布区内的岩层变形不协调,连续性遭到破坏,出现离层情况;厚硬层位下部离层,而上部保持连续,其在此时承担了其上部地层的应力,是应力集中的区域。在开采至110、270 m时,不平衡力突破厚硬层位,地应力得到释放,可能是导致剧烈来压的重要原因。
根据上述计算结果及分析,可以获得整个开采过程中岩体受工程扰动后的不平衡力分布,进而得知出现变形不协调的范围大小及变化过程,可以理解为开采扰动产生的垮落带、裂隙带影响范围;同时,可以通过不平衡力发展是否贯穿某一岩层来判定此岩层的断裂情况,为采场的来压控制、预先水力压裂、加固支护等提供理论依据。
3.3 模型试验验证
将上述回采过程在实验台上进行小尺寸模拟验证,依据相似模拟理论确定本次物理相似模拟的各项参数选取如下:

几何相似比:CL=lm/lp=1∶200
密度相似比:Cρ=ρm/ρp=1∶1.60
应力相似比:Cσ=σm/σp=1∶320
泊松比为1∶1。其中,lm为模型尺寸;lp为原型尺寸;m为模型密度;p为原型密度;m为模型应力;p为原型应力。相似模拟采用与表1、2完全一致的岩层厚度及岩性条件,模型尺寸为2 500 mm×1 500 mm×200 mm,模拟工作面走向500 m范围内的回采过程。用钢锥从左向右以5 cm/次的开采步距进行回采,在开采15 cm时直接顶尚未垮落,将2个微型液压支架并排放入刚挖好的回采空间,关闭泄压阀,手动按压活塞手柄加压撑起支架顶梁直至与直接顶完全接触,并将在每个开采步距结束后向前移架5 cm,模型及支架如图11所示。

图11 模型及液压支架示意
Fig.11 Schematic of model and hydraulic support
在整体开采过程中,模型分别于工作面推进112.6、176.1 cm处发生顶板岩层破断,支架监测阻力如图12所示,对应岩层破断形式如图13所示。

图12 支架阻力随采变化规律
Fig.12 Variety of support resistance during the mining process

图13 模型试验顶板破坏情况
Fig.13 Fracture of hard roof in model test
模型试验结果中,工作面发生了2次厚硬层位破断导致的强来压,规律与数值计算结果基本保持一致。
3.4 现场实测资料分析
同忻煤矿8103工作面紧邻8102工作面,具有近似地质情况及开采过程,采用其实测来压情况作为数值模拟的验证。
实测结果表明,8103工作面推进至127.5 m时发生初次来压,来压期间部分支架立柱最大下缩量达到0.5 m,安全阀开启率达到76%,中部区域顶煤破碎,有炸帮现象,工作面来压强烈;当工作面推进至194.95 m时,工作面出现周期来压,周期来压步距为67.45 m,工作面来压较为强烈,机道局部顶煤破碎;当工作面推进至211 m时,工作面再次出现周期来压,支架最大工作阻力达到15 500 kN,工作面来压强度为中等。8103工作面初采阶段来压步距情况见表3。数值模拟结果的初次来压位置与8103工作面实测资料基本一致,进一步验证了数值计算结果的合理性。
表3 8103工作面来压位置及来压步距
Table 3 Weighting interval and position of No.8103 working face

来压次数推进距离/m来压步距/m1127.50127.502194.9567.453211.0016.054254.1043.105301.6547.556322.8021.157353.4030.608385.8532.459417.8031.9510435.5517.7511473.4537.9012499.5026.0513529.1029.60
注:初次来压步距127.5m,平均周期来压步距33.46 m。
4 结 论
(1)连续性结构的变形不协调问题可以转换为连续介质力学边值问题分析解的存在性问题。计算有解时,结构能够保持连续;计算无解时,平衡条件、变形协调条件及本构关系无法同时满足,将出现变形不协调情况,体现为结构的开裂、破坏。
(2)通过引入黏塑性模型对过应力的处理方式,经典弹塑性理论可扩展至屈服面外,平衡应力场与屈服应力场的差值称为不平衡应力场,对应的等效节点力称为不平衡力。不平衡力是结构偏离平衡位置的度量,不平衡力为0时结构能够同时满足平衡条件、变形协调条件及本构关系,结构保持连续性;不平衡力不为0时,其位置和大小可以用于指示结构变形不协调部位,进而判断结构开裂、破坏情况。
(3)数值模拟结果表明,开采过程中不平衡力首先集中在近场的层间,之后因层间变形不协调影响而向上部岩层发展;不平衡力分布范围总体和开采推进距离相关,其分布高度同时会受厚硬层位影响,煤层上方48.87 m处厚度16.05 m的13号岩层、煤层上方93.37 m处厚度20.25 m的19号岩层两个厚硬层位对不平衡力分布区域起阶段性控制作用。
(4)在开采至110、270 m时,不平衡力分布区贯穿并突破厚硬层位向上发展,地应力得到释放,可能是导致剧烈来压的重要原因。数值模拟结果得到了模型试验及现场实测数据的验证,可为顶板控制来压分析、预先水力压裂层位选择等方面提供数据支撑。
[1] 钱鸣高,缪协兴,何富连.采场“砌体梁”结构的关键块分析[J].煤炭学报,1994,19(6):557-563.
QIAN Minggao,MIAO Xiexing,HE Fulian.Analysis of key block in the structure of voussoir beam in longwall mining[J].Journal of China Coal Society,1994,19(6):557-563.
[2] 钱鸣高,缪协兴,许家林.岩层控制中的关键层理论研究[J].煤炭学报,1996,21(3):2-7.
QIAN Minggao,MIAO Xiexing,XU Jialin.Theoretical study of key stratum in ground control[J].Journal of China Coal Society,1996,21(3):2-7.
[3] 黄庆享,钱鸣高,石平五.浅埋煤层采场老顶周期来压的结构分析[J].煤炭学报,1999,24(6):581-585.
HUANG Qingxiang,QIAN Minggao,SHI Pingwu.Structural analysis of main roof stability during periodic weighting in long wall face[J].Journal of China Coal Society,1999,24(6):581-585.
[4] 宋振骐,蒋宇静,刘建康.“实用矿山压力控制”的理论和模型[J].煤炭科技,2017,150(2):1-10.
SONG Zhenqi,JIANG Yujing,LIU Jiankang.Theory and model of “practical method of mine pressure control”[J].Coal Science &Technology Magazine,2017,150(2):1-10.
[5] 姜福兴.采场覆岩空间结构观点及其应用研究[J].采矿与安全工程学报,2006,23(1):30-33.
JIANG Fuxing.Viewpoint of spatial structures of overlying strata and its application in coal mine[J].Journal of Mining &Safety Engineering,2006,23(1):30-33.
[6] LU Cunjin,XU Jinpeng,ZHAO Heng,et al.Floor disturbance and failure characteristics of super-large mining height working face[J].Geofluids,2022,2022:1-13.
[7] LU Yiyu,GONG Tao ,XIA Binwei,et al.Target stratum determina-tion of surface hydraulic fracturing for far-field hard roof control in underground extra-thick coal extraction:A case study[J].Rock Mechanics &Rock Engineering,2018,52(8):2725-2740.
[8] 李杨,任玉琦,王楠,等.采空区垮落顶板形态及其演化特征[J].煤炭学报,2021,46(12):3771-3780.
LI Yang,REN Yuqi,WANG Nan,et al.Structure form and evolution characteristics of collapsed roof in goaf[J].Journal of China Coal Society,2021,46(12):3771-3780.
[9] REN Fengyu,ZHANG Dongjie,CAO Jianli,et al.Study on the rock
mass caving and surface subsidence mechanism based on an in situ geological investigation and numerical analysis[J].Mathematical Problems in Engineering,2018,2018:1-18.
[10] 付玉平,宋选民,邢平伟.浅埋煤层大采高超长工作面垮落带高度的研究[J].采矿与安全工程学报,2010,27(2):190-194.
FU Yuping,SONG Xuanmin,XING Pingwei.Study of the mining height of caving zone in large mining height and super-long face of shallow seam[J].Journal of Mining &Safety Engineering,2010,27(2):190-194.
[11] 吕进国,姜耀东,李守国,等.巨厚坚硬顶板条件下断层诱冲特征及机制[J].煤炭学报,2014,39(10):1961-1969.
LÜ Jinguo,JIANG Yaodong,LI Shouguo,et al.Characteristics and mechanism research of coal bumps induced by faults based on extra thick and hard roof[J].Journal of China Coal Society,2014,39(10):1961-1969.
[12] 张杰,杨相海.采场覆岩的流固耦合损伤分析[J].西安科技大学学报,2010,30(2):141-144,149.
ZHANG Jie,YANG Xianghai.Liquid-solid coupling damage influence of coal roof[J].Journal of Xi’an University of Science and Technology,2010,30(2):141-144,149.
[13] 孙琪皓,马凤山,赵海军,等.基于渗流-损伤-应力耦合作用下考虑力学参数弱化的巷道围岩变形破坏分析[J].工程地质学报,2019,27(5):955-965.
SUN Qihao,MA Fengshan,ZHAO Haijun,et al.Deformation and failure of surrounding rock considering weakening of mechanical parameters under seepage-damage-stress coupling[J].Journal of Engineering Geology,2019,27(5):955-965.
[14] 陈灿,刘贤,肖洪天.塔山煤矿坚硬顶板水力压裂裂缝扩展规律研究[J].矿业研究与开发,2020,40(9):75-80.
CHEN Can,LIU Xian,XIAO Hongtian.Study of fracture propagation law of hydraulic fracturing in hard roof of Tashan coal mine[J].Mining Research and Development,2020,40(9):75-80.
[15] 郭历伦,陈忠富,罗景润,等.扩展有限元方法及应用综述[J].力学季刊,2011,32(4):612-625.
GUO Lilun,CHEN Zhongfu,LUO Jingrun,et al.A review of the extended finite element method and its applications[J].Chinese Quarterly of Mechanics,2011,32(4):612-625.
[16] 杨强,王守光,李超毅,等.岩体结构变形破坏的内在驱动力-不平衡力[J].工程地质学报,2020,28(2):202-210.
YANG Qiang,WANG Shouguang,LI Chaoyi,et al.Internal driving force of deformation and failure of rock mass structure-unbalanced force[J].Journal of Engineering Geology,2020,28(2):202-210.
[17] 杨强,薛利军,王仁坤,等.岩体变形加固理论及非平衡态弹塑性力学[J].岩石力学与工程学报,2005,24(20):106-114.
YANG Qiang,XUE Lijun,WANG Renkun,et al.Reinforcement theory considering deformation mechanism of rock mass and non-equlibriem elasto-plastic mechanics[J].Chinese Journal of Rock Mechanics and Engineering,2005,24(20):106-114.
[18] 杨强,冷旷代,刘耀儒.变形加固理论的力学基础与工程意义[J].岩土力学,2011,32(1):1-8.
YANG Qiang,LENG Kuangdai,LIU Yaoru.Mechanical basis and engineering significance of deformation reinforcement theory[J].Rock and Soil Mechanics,2011,32(1):1-8.
[19] 杨强,陈新,周维垣.基于D-P准则的三维弹塑性有限元增量计算的有效算法[J].岩土工程学报,2002,24(1):16-20.
YANG Qiang,CHEN Xin,ZHOU Weiyuan.A practical 3D elasto-plastic incremental method in FEM based on D-P yield criteria[J].Chinese Journal of Geotechnical Engineering,2002,24(1):16-20.
[20] DUVANT G,LIONS J L.Inequalities in mechanics and physics[M].Berlin:Springer,1976.
[21] MACARI E J,WEIHE S,ARDUINO P.Implicit integration of elastoplastic constitutive models for frictional materials with highly non-linear hardening functions[J].Mechanics of Cohesive-Frictional Materials,1997,2(1):1-29.
[22] YANG Qiang,LENG Kuangdai,CHANG Qiang,et al.Failure me-
chanism and control of geotechnical structures[M].Berlin:Springer,2013:63-87.
[23] ZIENKIEWICZ O C,HUMPHESON C,LEWIS R W.Associated and non-associated visco-plasticity and plasticity in soil mechanics[J].Geotechnique,1975,25(4):674-689.
[24] CHABOCHE J L.A review of some plasticity and viscoplasticity constitutive theories[J].International Journal of Plasticity,2008,24(10):1642-1693.
[25] 冷旷代.岩体结构非平衡演化稳定与控制理论基础研究[D].北京:清华大学,2013.
LENG Kuangdai.Research on the fundamentals of stability and control of non-equilibrium evolution of rock mass structures[D].Beijing:Tsinghua University,2013.
[26] DENG J Q,YANG Q,LIU Y R,et al.3D finite element modeling of directional hydraulic fracturing based on deformation reinforcement theory[J].Computers and Geotechnics,2018,94:118-133.
[27] 程立,刘耀儒,吕庆超,等.特高拱坝非平衡演化的变形稳定控制理论及应用[J].水力发电,2019,45(10):53-58,115.
CHENG Li,LIU Yaoru,LÜ Qingchao,et al.Theory and application of deformation stability control of non-equilibrium evolution for super high arch dams[J].Water Power,2019,45(10):53-58,115.
[28] 于斌,朱卫兵,高瑞,等.特厚煤层综放开采大空间采场覆岩结构及作用机制[J].煤炭学报,2016,41(3):571-580.
YU Bin,ZHU Weibing,GAO Rui,et al.Strata structure and its effect mechanism of large space stope for fully-mechanized sublevel caving mining of extremely thick coal seam[J].Journal of China Coal Society,2016,41(3):571-580.
[29] 蒋金泉,张培鹏,聂礼生,等.高位硬厚岩层破断规律及其动力响应分析[J].岩石力学与工程学报,2014,33(7):1366-1374.
JIANG Jinquan,ZHANG Peipeng,NIE Lisheng,et al.Fracturing and dynamic response of high and thick stratas of hard rocks[J].Chinese Journal of Rock Mechanics and Engineering,2014,33(7):1366-1374.
