随着低碳环保、节能减排等政策的深入实施，要求在矿产资源开发全过程中，必须实施科学有序开采，使矿区及周边生态环境扰动在可控范围内，以实现环境生态化、开采方式科学化、资源利用高效化、管理信息数字化、矿区社区和谐化的绿色矿山建设目标。煤炭作为我国主体能源，在保障国家能源安全的同时，垮落式管理顶板的地下开采方法也造成了大面积的地表塌陷和环境损伤破坏。1985年辽宁工程技术大学与抚顺矿务局合作，在老虎台矿进行正式的覆岩离层注浆试验并取得成功[1]，杨伦[2]进一步分析了老虎台矿特定的地质采矿条件下，特厚绿色页岩层遇水破碎的膨胀特性及其支撑上覆岩层的效果；表明实施采动覆岩离层注浆，既可以有效解决粉煤灰、矿渣等废弃物的堆存占地及其诱发的次生灾害问题，又可以一定程度地控制覆岩与地表下沉。

国内外学者从不同角度对覆岩移动规律和离层发育规律开展研究，包括地面钻孔观测、数值模拟、相似材料模型实验、理论分析等。PALCHIK[3-4]通过地面钻孔利用橡胶塞封堵，分段测量钻孔内的瓦斯溢出情况，进一步判断覆岩破坏带高度和水平离层层位；滕永海等[5]通过地面钻孔设置压缩木以确定离层层位和离层发育规律；YU等[6]通过地面钻孔电视实测分析覆岩的移动破坏规律。CHEN和GUO利用Cosserat理论数值模拟长壁开采覆岩离层的演化规律并分析岩性的影响[7]；苏仲杰等[8]采用RFPA仿真软件模拟覆岩离层；WANG等[9]采用UDEC分析上覆岩层移动和离层特征；郭惟嘉等[10]将层状岩体视为各向同性材料，采用富氏积分变换得出了水平煤层开采覆岩离层的解析表达式，并采用黏弹性力学模型进行离层的数值模拟分析。YE Qing和ZHAO Pengxiang等[11-12]利用相似材料模型实验研究上覆岩层采动裂隙发展演化特征；钱鸣高、许家林、鞠金峰等研究提出了岩层控制的关键层理论[13]，构建了覆岩关键层位置的判别方法[14]，分析了关键层运动对及地表移动影响以及离层演化规律[15-16]，并开展覆岩离层注浆减沉钻孔的布置等系列研究[17-18]；吴侃等[19]将岩体视为弹脆性体，岩体移动变形为刚性位移加弹性变形，通过建立采空区上方已破裂岩体与顶板压力之间的关系，搭建基于多组合梁的岩体内部破坏过程动态力学模型，实现了覆岩离层随断裂带高度发展的跳跃、张闭等演化过程计算可视化；上述研究对认识采动覆岩移动规律和离层孕育、发生、发展的演化过程起到了积极的推动作用。

然而，地面钻孔观测施测周期长、费用高；相似材料模型实验因受模型尺寸和相似条件限制、误差影响等还难以做到定量模拟[20]。而数值模拟和理论分析因涉及众多物理力学参数[21]，分析过程复杂，结果也不尽人意；一般用于离层位置识别，难以给出离层量。大量的研究表明，采动覆岩移动与地表移动规律具有相似性，都是因地下开采后原有应力平衡被打破，在获取新的平衡过程中的必然反映；如果从覆岩与地表等效下沉出发，能够建立采动覆岩与地表下沉的关系模型，就可实现覆岩与地表采动下沉计算的统一；进而利用上覆岩层的结构特征，定量确定覆岩离层层位和离层量，可以为覆岩离层注浆减沉设计提供一定的技术支持。

1 采动覆岩与地表下沉的关系模型

1.1 研究共识

开采沉陷理论与实践研究表明，地下资源开采后，上覆岩层与地表的移动方向指向采空区中心[22-23]；且当不考虑垮落破碎岩石的碎胀性时，下沉主断面上地表下沉面积与任一水平的覆岩下沉面积相等[22-24]。采动覆岩移动变形与破坏的传递过程与上覆岩层的岩性密切相关[25]，不同岩层的边界角不同；对于按覆岩与地表移动边界角确定的主要影响半径，研究认为可以用式(1) [26]表示：

(1)

其中，rz为按覆岩边界角确定的z水平主要影响半径，m；H为开采深度，m；z为某一岩层的埋藏深度，m；r0为按地表边界角δ0确定的地表主要影响半径，m；q为与上覆岩层力学性质及组合有关的参数。尽管当q>1或q<1时，覆岩与地表的主要影响半径呈非线性变化，可以反映上覆岩层的岩性影响；但为实际分析方便，可取q=1，即按线性规律确定采动覆岩与地表移动的主要影响半径关系，如图1所示。

1.2 采动覆岩与地表下沉关系模型

对于如图2所示的采动覆岩与地表移动，地表采动影响的半盆地长r可表示为

(2)

式中，b为工作面宽度，m；hi为从地表向下第i层岩土层的厚度，m，i=1,2,3,…,n，当i=1时，h1为表土层厚度，m。

以地表下沉盆地中心Oo为坐标原点，地表某点Po的坐标为xo，其下沉可表示为wo(xo)；地表点Po移动方向上对应的某一水平的覆岩点为Pjs，其坐标为点的下沉可表示为对于如图1所示的近水平地层，根据几何相似性，地表点Po和覆岩内部点的坐标关系可表示为

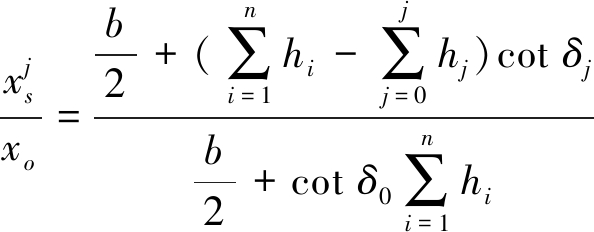
(3)

其中，为上覆岩土层的累计厚度，等于开采深度为预计算的覆岩水平，j=0,1,2,…,n；δj为第j层岩土层的边界角。当j=0时，h0=0代表的计算水平是地表；当j=1时，代表的计算水平是地表下第1层岩层的上界面。

对于地表和覆岩内的微小坐标单元dxo和根据其对应的地表下沉面积和覆岩下沉面积相等的研究共识，可得

(4)

从而有

(5)

将式(3)求导代入式(5)，可得地表点xo与对应覆岩内部点的下沉存在如下关系：

(6)

根据覆岩与地表主要影响半径可以按线性规律处理的研究共识，可取

δ0=δj

(7)

将式(7)代入式(6)，整理后可得式(8)表示的采动覆岩与地表下沉关系模型。

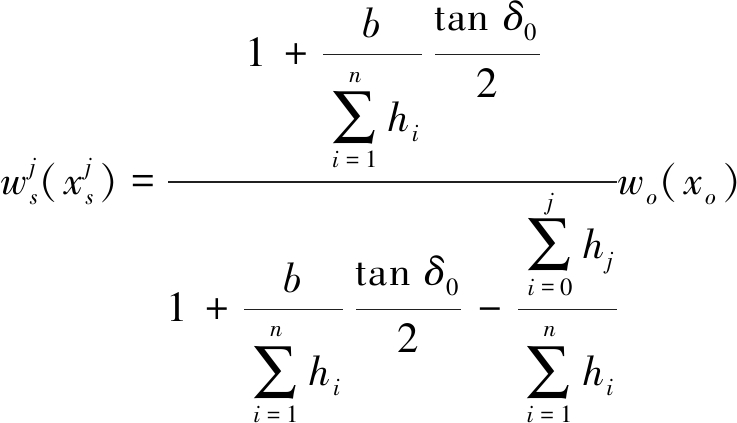
(8)

其中，b/H为开采宽度与开采深度的比值，简称宽深比，表示了该工作面的采动程度。当xo=0时，对应的是下沉盆地中心OoOs铅锤线，该线上的覆岩与地表下沉量最大。

当时，φ0为充分采动角，(°)，开采达到临界充分采动,此时开采宽度记为bl，地表下沉盆地中心点Oo的下沉达到该地质采矿条件下的最大下沉值，如图3(a)所示。当开采宽度时，开采达到超充分采动，地表下沉盆地中心出现平底，平底长度L=b-bl，如图3(b)所示，该段的地表下沉等于临界充分采动的地表最大下沉；其余地表的采动沉陷按坐标平移L/2、取临界充分采动的开采宽度bl进行计算，可以实现采动覆岩与地表从不充分、临界充分到超充分的全过程推演计算。

1.3 覆岩与地表下沉关系的分析讨论

为不失一般性，覆岩与地表采动影响边界角分别取65°、60°和55°，开采的宽深比分别取0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9和1.0，对不同埋藏深度的覆岩下沉与地表下沉关系进行分析。

当边界角为65°时，依据式(8)计算的采动覆岩与地表的下沉关系见表1。由表1可知，从顶板、上覆岩层到地表，采动下沉呈递减分布规律，越靠近采空区的覆岩，下沉越大。当宽深比等于0.2时，顶板下沉是地表下沉的5.66倍，地表下沉率为0.18；当宽深比增加到1.0时，顶板与地表下沉比减小至1.93，地表下沉率增加至0.52。随着宽深比的增加，采动程度增大，覆岩下沉与地表下沉的比值减小，表明地表下沉随着采动程度的增加而增大。

保持其他条件不变，当覆岩与地表移动的边界角减小到60°时，由表1可知，当宽深比等于0.2时，顶板下沉是地表下沉的6.77倍，地表下沉率为0.15；当宽深比增加到1.0时，顶板与地表的下沉比为2.15，即地表下沉率为0.47。表明随着边界角的减小，地表移动范围增大，地表下沉值减小。

当边界角进一步减小至55°时，由表1可知，当宽深比等于0.2时，顶板下沉与地表下沉的比值进一步增大至8.00，地表下沉率为0.13；当宽深比增加到1.0时，顶板下沉与地表下沉的比值进一步增大至2.40，地表下沉率为0.42。说明随着边界角的减小，地表移动范围进一步增大，地表下沉值也随之进一步减小。

对比分析表1发现，采动覆岩与地表下沉关系受控于宽深比和边界角，随着宽深比的增大，采动程度增加，覆岩与地表的下沉比值减小，地表下沉增大；随着边界角的减小，采动影响范围增大，覆岩与地表的下沉比值增大，地表下沉值减小。地表下沉率随采动程度和边界角的变化见表2，表明覆岩与地表的采动下沉规律符合开采沉陷的一般规律。

2 采动覆岩与地表下沉关系的实测结果验证

澳大利亚悉尼盆地的Southern煤田Bulli煤层204号工作面，采用后退式长壁开采，煤层近水平，平均开采厚度2.5 m，工作面宽度192 m，开采深度483 m，宽深比0.4[22]；悉尼盆地的Newcastle煤田的Great煤层2号工作面，煤层近水平，平均开采厚度3.5 m，工作面宽度150 m，开采深度470 m，宽深比0.4[23]；Bulli煤层204号工作面和Great煤层2号工作面均通过地面钻孔，采用压缩木实施覆岩内部观测，具体覆岩结构与岩性情况不详。KOLEBAEVA[27]在前苏联的Donetsk煤田通过地面观测线和钻孔压缩木观测相结合的方式，对煤层倾角28°的倾斜煤层开采的覆岩与地表下沉进行了观测，开采厚度1.25 m，开采宽度123 m，开采深度107 m，宽深比1.15；上覆岩层中除距地表深25 m处有一厚4 m的砂岩外，其他均为弱岩层。由于覆岩与地表移动的边界角不详，且Southern煤田和Newcastle煤田均位于悉尼盆地，故Bulli煤层204号工作面和Great煤层2号工作面的边界角试取值65°；而Donetsk开采工作面的边界角试取值50°；计算的不同深度覆岩与地表下沉比值与实测比值的对比如图4所示。由图4可知，除Great煤层的深部覆岩有一定偏差外，其余皆吻合较好，表明基于等效下沉的采动覆岩与地表下沉关系模型具有一定的适用性。

3 采动覆岩离层的计算与识别

3.1 采动覆岩离层计算方法

理论上，由式(8)可计算出给定地质采矿条件下任一深度采动覆岩和地表的下沉。但由于煤系地层呈层分布，同一岩层是一个整体，其采动下沉具有一致性；实际计算时，须按钻孔揭示的实际岩层赋存状态，从顶板、上覆岩层到地表依次计算各岩层的下沉值；利用两相邻岩层下沉的非一致性，即可估算出上覆岩层中的离层量和并确定离层层位。由于地表下沉盆地中心Oo的下沉量最大，故最大离层量应出现在OoOs铅锤线上，实际计算时取

3.2 采动覆岩无效离层的识别与剔除

通常情况下，地下开采引起的覆岩与地表移动破坏具有分区性，包括垮落带、断裂带和整体弯曲下沉带[28]，如图5(a)所示。采动覆岩是否能形成标准的“三带”结构，取决于开采厚度、开采深度以及上覆岩层的基岩厚度、岩层的组合和力学性质等地质采矿条件；当开采厚度大、基岩厚度小、采深小时，上覆岩层与地表可能不存在整体弯沉带，如图5(b)所示，甚至只有垮落带，如图5(c)所示。

由于垮落带、断裂带内岩体破碎，其中的裂隙、空隙等与工作面连通，无法形成封闭的充填空间。因此，有效注浆层位的确定，应结合上覆岩层的力学性质，利用“三下”采煤规范中的经验公式[20,29]，见表3，计算出导水裂隙带高度，以剔除位于导水裂隙带内无法形成封闭充填空间的无效离层。

4 采动覆岩离层的模拟计算与分析

假设开采工作面宽80 m，走向达到充分采动，开采深度200 m，宽深比为0.4；开采厚度2 m，煤层倾角3°，取覆岩与地表移动的边界角为65°。上覆岩层的岩性自地表向下分别为表土层、泥岩、砂岩、页岩、砂质泥岩及互层等；以砂岩、粉砂岩为主，单向抗拉强度为55 MPa，属坚硬岩层。为分析方便，仅展示目标段第24～40层岩层的采动下沉模拟计算结果；各岩层的岩性、厚度、累计深度分别见表4第2、3、4列所示。

4.1 采动覆岩与地表下沉计算。

煤层开采后，采动下沉自顶板向上覆岩层传递，顶板以垮落形式堆积于采空区，顶板下沉为2 000 mm，等于煤层开采厚度。利用式(8)计算各岩层的下沉量，见表4中的第5列。

4.2 采动覆岩离层量计算

由于不同层位岩层下沉的非一致性，下位岩层的下沉量减去上位岩层的下沉量，即为两相邻岩层的离层量，见表4中的第6列。由表4可见，该上覆岩层中存在2个较大的离层。25号岩层为20 m厚的砂岩，计算下沉量为976 mm；其下覆岩层为4 m厚的泥岩，泥岩层的计算下沉量为1 101 mm，两岩层间的离层量将达到125 mm。而38号岩层为厚10 m的砂岩，计算下沉量为1 469 mm；其下覆岩层为3 m厚的页岩，页岩层的计算下沉量为1 607 mm，两岩层间的离层量将达到138 mm。

4.3 采动覆岩无效离层的识别与剔除

根据表3中的导水裂隙带高度经验公式，对于坚硬岩层，计算可得导水裂隙带高度为(45.45±8.9)m，取导水裂隙带高度上限值为54.35 m，表明38号砂岩位于该断裂带内，其下部离层无法形成有效的封闭充填空间，故不予考虑、应予剔除。由于25号厚砂岩位于导水裂隙带上限值之外，可将其下部离层作为覆岩离层注浆的可行层位，并开展覆岩离层注浆减沉设计。

4.4 分析与讨论

为定量对比相同条件下不同边界角对覆岩与地表下沉及离层的影响，进一步选取边界角为55°和60°，计算的覆岩与地表下沉如图6(a)所示、覆岩离层情况如图6(b)所示。由图6可见，当边界角从65°减小至60°、55°时，地表下沉从600 mm分别减小至515 mm和444 mm，表明边界角对地表及浅部岩层影响较大，对靠近顶板的上覆岩层影响较小；相对应的第25号20 m厚砂岩与下覆的第26号4 m厚泥岩间的离层量分别为125、125和122 mm，几乎没有变化，离层量约为开采厚度的6.25%。

模拟计算结果表明，利用基于等效下沉的覆岩与地表下沉关系模型计算覆岩离层，不涉及各岩层的物理力学特性，仅与工作面宽度、开采深度、岩层厚度、岩层埋藏深度、覆岩与地表移动的边界角等确定性参数有关，计算过程简便，基本能反映岩层结构、采动程度对覆岩与地表下沉及离层发育的影响规律。

但由于笔者建立的采动覆岩与地表下沉关系模型及离层估算方法，是基于沉陷主断面上地表下沉与任一水平的覆岩下沉面积相等，且不考虑垮落破碎岩石碎胀性的影响，与采动覆岩与地表的实际移动变形与破坏尚存一定的不符。

(1)采动覆岩与地表移动既取决于采动程度，也受控于上覆岩层的物理力学性质。理论上，上覆岩层中的厚硬岩层对覆岩与地表移动规律起控制作用，文中只考虑了岩层厚度，未考虑岩层的强度，实际应用中尚需进一步完善。

(2)受成煤条件和聚煤规律影响，煤层倾斜和地表起伏的煤炭资源赋存条件广泛存在。文中仅分析了近水平煤层和地表水平的开采情况，对于倾斜煤层和地表倾斜情况，可参考文献[30-31]，基于等价变形和光束投影进行深入研究。

(3)采动覆岩与地表移动规律及离层发育演化随工作面推进过程而动态发展，也存在一定的跳跃突变[19]，文中研究针对的是开采稳定后的终态，未考虑随开采工作面推进的时间发展过程[32]，未来仍需进一步改进。

(4)基于主断面上等效下沉建立的覆岩与地表下沉关系模型，尚未兼顾垮落带、断裂带内垮落、破碎岩石的碎胀性及其对上覆岩层和地表移动的影响，这与采动覆岩移动破坏的实际结果不符，后续研究应结合“三带”分布规律予以完善。

5 结 论

(1)基于采动覆岩与地表移动指向采空区中心、移动边界可简化为直线的线性边界和主断面上地表下沉和覆岩下沉面积相等的研究共识，建立了采动覆岩与地表下沉的统一关系模型，定量分析了边界角、开采宽度、开采深度、岩层厚度对覆岩与地表下沉的影响规律。

(2)根据煤系地层岩层的层状沉积特征，同一岩层具有相对完整性和下沉一致性特点，通过逐层计算各岩层的下沉，可以定量估算两相邻岩层间的离层量，计算方法简单、便捷。

(3)根据上覆岩层的岩性，利用规范给定的经验公式，可确定给定地质采矿条件下的导水裂隙带高度，用以剔除位于该断裂带内无法形成封闭空间的无效离层，进而优选出可行的覆岩离层注浆层位，为覆岩离层注浆减沉设计提供了技术依据。

(4)尽管基于等效下沉建立了采动覆岩与地表下沉关系模型，并用于覆岩离层量估算；但由于该模型是一个几何模型，既未考虑覆岩强度等物理力学特性以及岩性组合，也未涉及煤层倾斜与地表倾斜、开采时间过程以及冒落破碎岩石的碎胀性等情况，尚需在后续研究中进一步改进和完善。

参考文献（References）:

[1] 杨伦.对采动覆岩离层注浆减沉技术的再认识[J].煤炭学报,2002,27(4):352-356.

YANG Lun.Re-understand the technology of reducing the subsidence due to mining by injecting grouts into separated beds in overlying disrupted strata by extraction[J].Journal of China Coal Society,2002,27(4):352-356.

[2] 杨伦.我国首例离层注浆减沉试验的再思考[J].中国地质灾害与防治学报,2006,17(1):102-104.

YANG Lun.Re-thinking about the first subsidence reducing test of injecting grout into separated beds in China[J].The Chinese Journal of Geological Hazard and Control,2006,17(1):102-104.

[3] PALCHIK V.Formation of fractured zones in overburden due to longwall mining[J].Environmental Geology,2003,44:28-38.

[4] PALCHIK V.Localization of mining-induced horizontal fractures along rock layer interfaces in overburden:Field measurements and prediction[J].Environmental Geology,2005,48:68-80.

[5] 滕永海,阎振斌.采动过程中覆岩离层发育规律的研究[J].煤炭学报,1999,24(1):25-28.

TENG Yonghai,YAN Zhenbin.Study on law of overburden split development in mining process[J].Journal of China Coal Society,1999,24(1):25-28.

[6] YU Bin,ZHAO Jun,KUANG Tiejun,et al.In situ investigations into overburden failures of a super-thick coal seam for longwall top coal caving[J].International Journal of Rock Mechanics &Mining Sciences,2015,78:166-162.

[7] CHEN Shougen,GUO Hua.Numerical simulation of bed separati-on development and grout injecting into separations[J].Geotechnical and Geological Engineering,2008,26:375-385.

[8] 苏仲杰,于广明,杨伦.覆岩离层变形力学机理数值模拟研究[J].岩石力学与工程学报,2003,22(8):1287-1290.

SU Zhongjie,YU Guangming,YANG Lun.Numerical simulation on mechanism of deformation of separation strata in overburden[J].Chinese Journal of Rock Mechanics and Engineering,2003,22(8):1287-1290.

[9] WANG Shaofeng,LI Xibing,WANG Shanyong.Separation and fracturing in overlying strata disturbed by longwall mining in a mineral deposit seam[J].Engineering Geology,2017,226:257-266.

[10] 郭惟嘉,刘立民,沈光寒,等.采动覆岩离层性确定方法及离层规律的研究[J].煤炭学报,1995,20(1):39-44.

GUO Weijia,LIU Limin,SHEN Guanghan,et al.Determination of overburden separation and their rules after coal mining[J].Journal of China Coal Society,1995,20(1):39-44.

[11] YE Qing,WANG Geoff,JIA Zhenzhen,et al.Similarity simulation of mining-crack-evolution characteristics of overburden strata in deep coal mining with large dip[J].Journal of Petroleum Science and Engineering,2018,165:477-487.

[12] ZHAO Pengxiang,ZHUO Risheng,LI Shugang,et al.Analysis of advancing speed effect in gas safety extraction channels and pressure-relief gas extraction[J].Fuel,2020,265：116825.

[13] 钱鸣高,缪协兴,许家林,等.岩层控制的关键层理论[M].徐州:中国矿业大学出版社,2003.

[14] 许家林,钱鸣高.覆岩关键层位置的判别方法[J].中国矿业大学学报,2000,29(5):463-467.

XU Jialin,QIAN Minggao.Method to distinguish key strata in overburden[J].Journal of China University of Mining &Technology,2000,29(5):463-467.

[15] 许家林,钱鸣高.关键层运动对覆岩及地表移动影响的研究[J].煤炭学报,2000,25(2):122-126.

XU Jialin,QIAN Minggao.Study on the influence of key strata movement on subsidence[J].Journal of China Coal Society,2000,25(2):122-126.

[16] 许家林,钱鸣高,金宏伟.岩层移动离层演化规律及其应用研究[J].岩土工程学报,2004,26(5):632-636.

XU Jialin,QIAN Minggao,JIN Hongwei.Study and application of bed separation distribution and development in the process of strata movement[J].Chinese Journal of Geotechnical Engineering,2004,26(5):632-636.

[17] 许家林,钱鸣高.覆岩注浆减沉钻孔布置的试验研究[J].中国矿业大学学报,1998,27(3):276-279.

XU Jialin,QIAN Minggao.Study on layout of grouting boreholes for retarding stratum subsidence[J].Journal of China University of Mining &Technology,2004,26(5):632-636.

[18] JU Jinfeng,XU Jialin.Structural characteristics of key strata and strata behavior of a fully mechanized longwall face with 7.0 m height chocks[J].International Journal of Rock Mechanics &Mining Sciences,2013,58:46-54.

[19] 吴侃,王悦汉,邓喀中.采空区上覆岩层移动破坏动态力学模型的应用[J].中国矿业大学学报,2000,29(1):34-36.

WU Kan,WANG Yuehan,DENG Kazhong.Application of dynamic mechanics model of overlying strata movement and damage above goaf[J].Journal of China University of Mining &Technology,2000,29(1):34-36.

[20] MIAO Xiexing,CUI Ximin,WANG Jin’an,et al.The height of fractured water-conducting zone in undermined rock strata[J].Engineering Geology,2011,120:32-39.

[21] 崔希民,邓喀中.煤矿开采沉陷预计理论与方法研究评述[J].煤炭科学技术,2017,45(1):160-169.

CUI Ximin,DENG Kazhong.Research review of predicting theory and method for coal mining subsidence[J].Coal Science and Technology,2017,45(1):160-169.

[22] KRATZSCH H.Mining subsidence engineering[M].Ber-

lin:Springer,1983.

[23] SHU D M,BHATTACHARYYA A K.Relationship between sub-surface and surface subsidence—A theoretical model [J].Mining Science and Technology,1990,11:307-319.

[24] SHU D M,BHATTACHARYYA A K.Prediction of sub-surface

movements due to underground coal mining [J].Geotechnical and Geological Engineering,1993,11:221-234.

[25] 郭文兵,白二虎,赵高博.高强度开采覆岩地表破坏及防控技术现状与进展[J].煤炭学报,2020,45(2):509-523.

GUO Wenbing,BAI Erhu,ZHAO Gaobo.Current status and progress on overburden and surface damage and prevention technology of high-intensity mining[J].Journal of China Coal Society,2020,45(2):509-523.

[26] 颜荣贵.地基开采沉陷与地表建筑[M].北京:冶金工业出版社,1995.

[27] KOLEBAEVA J M.Theory of ground movement in rock mass[M].

Moscow:Nedra,1968.

[28] JU Jinfeng,XU Jialin.Surface stepped subsidence related to top-

coal caving longwall mining of extremely thick coal seam under shallow cover [J].International Journal of Rock Mechanics &Mining Sciences,2015,78:27-35.

[29] 国家安全监管总局,国家煤矿安监局,国家能源局,等.建筑物水体铁路及主要井巷煤柱留设与压煤开采规范[S].北京:煤炭工业出版社,2017.

[30] 张华兴.倾斜煤层开采地表移动变形等价计算方法研究[J].煤炭科学技术,2020,48(10):119-123.

ZHANG Huaxing.Study on equivalent calculation method of surface subsidence in inclined coal seam mining[J].Coal Science and Technology,2020,48(10):119-123.

[31] SHU D M.Modification of subsidence parameters for sloping ground surfaces by the rays projection method[J].Geotechnical and Geological Engineering,1992,10:223-248.

[32] CUI Ximin,WANG Jiachen,LIU Yisheng.Prediction of progressive surface subsidence above longwall coal mining using a time function[J].International Journal of Rock Mechanics and Mining Science,2001,38(7):1057-1063.

Relationships between mining overburden rock and surface subidence and its application to estimate bed separation

CUI Ximin1,GAO Yu1,LI Peixian1,LI Zihao1,ZHANG Wenhao2,PENG Xiaozhan1,KANG Xinliang3

(1.College of Geoscience and Surveying Engineering,China University of Mining and Technology-Beijing,Beijing 100083,China;2.Technical Center,Xishan Coal Electricity Group Co.,Ltd.,Taiyuan 030053,China;3.Geology Department,Xishan Coal Electricity Group Co.,Ltd.,Taiyuan 030053,China)

Abstract:Underground mining may result in surface subsidence,infrastructure damage,land degradation and surface water accumulation,and cause the ecological deterioration.In order to control the surface and overburden rock strata movement and reduce the mining damage,the solid filling in goaf and overburden grout injection to bed separation are selected as useful techniques.The location of bed separation can be given by the traditional methods such as key strata theory,numerical simulation,similar tmaterial experiment and theoretical analysis.However,it is difficult to determine the quantitative value of bed separation because of its complicated calculation process,multiple physical and mechanical parameters and the effect of boundary conditions.The research results of mining subsidence demonstrate that the overburden and surface move towards to the goaf center along the ray projection,the subsidence boundary of overburden and surface can be simplified as straight line according to the synthetic limit angle and the surface subsidence area equals to any overburden strata subsidence area.Based on these research consensus about the characteristics of coal measure strata,the relationship model between mining overburden strata and surface subsidence have been established,which well reveals the evolution of overburden and surface subsidence with the synthetic limit angle,width of working face and mining depth.The ratio of mining overburden strata and surface subsidence increases with the increasing of burial depth for overburden strata,it reflects the transfer law of mining subsidence effect from roof to overburden and surface.When the width-depth ratio increases,the ratio of overburden-surface mining subsidence decreases and the surface subsidence increases.If the synthetic limit angle decreases,the range of surface subsidence increases and the corresponding surface subsidence decreases.The overburden rock strata and surface subsidence can be calculated layer by layer according to the actual strata thickness by borehole.For the subsidence inconsistency of two adjoining rock strata,the bed separation can be determined.It must be noted that the ineffective bed separation should be eliminate because it can’t form a closure filling space in the fractured zone.The maximum bed separation can be then optimized which is suitable for overburden grout injection.This identification and calculation method of bed separation is simple and convenient and helpful to the design of overburden grout injection.

Key words:rock strata thickness；bed separation；surface subsidence；overburden grout injection；equivalent subsidence

中图分类号:TD325

文献标志码:A

文章编号:0253-9993(2023)01-0074-09

移动阅读

收稿日期:2022-05-08

修回日期:2022-07-14

责任编辑:韩晋平

DOI:10.13225/j.cnki.jccs.W022.0677

基金项目:河北省自然科学基金生态智慧矿山联合基金资助项目(E2020402086)；国家自然科学基金资助项目(52274169)；中国矿业大学(北京)大学生创新训练基金资助项目(202202026)

作者简介:崔希民(1967—)，男，辽宁宽甸人，教授，博士生导师。Tel：010-62339996，E-mail：cxm@cumtb.edu.cn

引用格式:崔希民,高宇,李培现,等.采动覆岩与地表下沉关系模型及离层量估算方法[J].煤炭学报,2023,48(1):74-82.

CUI Ximin,GAO Yu,LI Peixian,et al.Relationships between mining overburden rock and surface subidence and its application to estimate bed separation[J].Journal of China Coal Society,2023,48(1):74-82.