随着我国井工煤矿开采深度逐年增加，加之软岩矿区与矿井分布广泛，出现了越来越多的困难巷道，围岩与支护体破坏严重，围岩大变形、持续流变等问题日益严峻[1-5]。
我国煤矿巷道80%以上是回采巷道，一般布置在煤层中，且经历开挖、稳定、受采动影响的全过程，采动应力高达2～5倍原岩应力，采动影响强烈。对于深部软岩回采巷道，一方面，煤矿进入深部开采后，地应力不断升高，软岩强度与地应力比值不断降低，导致软岩大范围塑性流动,其中扩容是巷道围岩变形的主要形式[6-7]；另一方面，回采巷道围岩变形主要发生在开挖阶段与受采煤工作面采动影响阶段，尤以后者为主。但随着巷道埋深增加，围岩流变效应逐渐凸显[8-9]，即使在稳定阶段，围岩仍以较大的速率变形。因此，深部软岩回采巷道大变形的主要原因是：围岩大范围的塑性流动和与时间有关的黏性流动。
岩石扩容是岩石在偏应力作用下体积发生膨胀的现象。自1949年BRIDGMAN首先观测到岩石的扩容现象后[10]，很多学者对岩石扩容性质、影响因素等进行了深入研究，并建立了多个岩石扩容力学模型[11-13]。研究发现岩石扩容主要发生在峰后，而且与岩石塑性变形和围压有密切关系。深部巷道大变形主要由围岩离层、结构面滑动、岩块转动及新裂纹产生等扩容变形引起，锚杆支护的主要作用是抑制锚固区围岩扩容变形，保持围岩的完整性[14-15]。
岩石流变是岩石应力-应变关系与时间因素相关的性质。软岩可看作一种非线性的黏弹塑性介质，软岩巷道围岩流变效应主要体现在两方面：一是围岩变形随时间增大；二是围岩强度随时间降低。巷道围岩变形与破坏并不是瞬间完成的，而是一个随时间不断变化和积累的过程。流变效应在深部软岩巷道中表现尤为突出[16-18]。
为有效控制深部软岩巷道围岩大变形，首先需揭示其变形与破坏机理，而建立描述围岩扩容、流变、损伤力学特性的本构模型是前提。然而，大多考虑流变的本构模型着重描述煤岩样在试验机恒载或分级加载条件下的应力-应变关系(特别是加速蠕变阶段)，而忽略煤岩样蠕变破坏后的力学响应，无法描述围岩峰后行为。但深部巷道开挖后围岩即出现峰后区并不断扩展，峰后围岩既是承载主体又是变形主体，其力学行为应重点考虑。因此，亟需建立可描述围岩峰后行为、充分考虑围岩力学特性的黏弹塑性本构模型。
笔者以我国煤矿典型深部软岩巷道-中煤新集口孜东矿千米深井软岩回采巷道为工程背景，基于实验数据、增量塑性流动理论和流变理论，改进并组合基本力学元件以描述围岩黏塑性力学特性，建立适合深部软岩巷道围岩变形与破坏特点的本构模型，推导其三维增量本构方程，并开发可供FLAC3D软件调用的数值形式。将该本构模型应用于口孜东矿121302孤岛工作面运输巷数值模拟，得到巷道围岩变形与破坏在掘进、流变和回采阶段的演化规律。通过对比数值模拟结果与井下实测数据，验证了该本构模型的科学性与合理性。
1 深部软岩巷道围岩本构模型
1.1 深部软岩巷道围岩力学特性
高地应力、围岩软弱和强采动是深部软岩回采巷道围岩大变形的三大原因，导致围岩劣化、扩容和流变效应凸显[19]。
巷道围岩劣化可分为依赖塑性变形的应变软化和依赖时间的流变损伤。扩容可分为塑性扩容(为与流变扩容区分，将增量塑性流动理论[20]中的扩容称为塑性扩容)和流变扩容[21-23]。巷道围岩流变还涉及蠕变3阶段和稳定与非稳定蠕变判别。因此，适用于深部软岩回采巷道分析的本构模型应能描述如图1所示的围岩力学特性。
图1 深部软岩巷道围岩变形和破坏特征与力学特性
Fig.1 Deformation and failure characteristics and mechanical properties of the soft surrounding rock of deep roadways
1.2 本构模型元件改进与组合
虽然弹性变形量在深部巷道围岩变形量中占比微小，但弹性性质贯穿围岩变形与破坏始末，弹性参数在塑性流动和流变变形计算中也发挥着重要作用，不可忽视。因此服从广义胡克定律的胡克体应作为本构模型的元件之一。
对于不依赖时间且主要发生在峰后的应变软化与塑性扩容，可采用应变软化塑性体描述。屈服条件随塑性变形增大而减弱，可实现应变软化；应用扩容角ψ>0°的非关联流动法则可实现塑性扩容。
在蠕变3阶段中，减速蠕变可采用由胡克体与牛顿体并联而成的凯尔文体描述；等速蠕变可采用牛顿体或由牛顿体与塑性体并联而成的理想黏塑性体描述，后者在前者的基础上考虑蠕变启动应力；加速蠕变的实现方式多样，主要有构建非线性元件，建立蠕变参数与时间或应力的函数关系，以及引入损伤力学理论3种方式[24]。
如图2所示，非稳定蠕变在荷载高于长期强度的情况下发生，反之发生稳定蠕变[25]。这涉及2个问题：① 非稳定蠕变过程中岩体强度随时间劣化，直至低于荷载发生破坏，即流变损伤；② 稳定蠕变过程中，变形随时间趋于极限。对于第1个问题，可采用将应变软化塑性体屈服条件与由荷载超过长期强度而产生的流变变形关联起来的方法解决。由荷载超过长期强度而产生的流变变形可采用改进黏塑性体描述，其中塑性体强度代表岩体长期强度。对于第2个问题，可根据蠕变终止曲线理论导出对模型中自由牛顿体(直接串联在模型中，无并联胡克体或塑性体)的限制条件，以给出稳定蠕变上限。
图2 稳定与非稳定蠕变
Fig.2 Steady and unsteady creep
根据前人研究成果，流变损伤有2个显著特点：① 在荷载高于长期强度的情况下发生[26]；② 损伤在减速和等速蠕变阶段缓慢累计，导致加速蠕变启动，而损伤主要发生在加速蠕变阶段[23,27]。此外，加速蠕变起点损伤量与常规压缩峰值点对应损伤量近似相等[24]，即减速和等速蠕变阶段损伤量与常规加载峰前损伤量相对应，而加速蠕变阶段损伤量与常规加载峰后损伤量相对应。因此，加速蠕变与流变损伤密不可分，可将黏塑性体中塑性体强度设为长期强度，黏塑性体变形量作为流变损伤参量。当损伤参量累计至某一阈值后，黏塑性体中牛顿体黏度开始随损伤参量增大而减小。考虑到损伤岩样有着更低的长期强度[28]，黏塑性体中塑性体强度也开始随损伤参量增大而减小，实现了流变损伤。与此同时，黏塑性体黏度和强度降低共同使加速蠕变显现。
与流变损伤类似，流变扩容也发生在荷载高于长期强度的情况[29]，因此可采用黏塑性体描述。流变扩容与塑性扩容都反映了围岩体积膨胀的现象，不同的是前者与时间有关。如前所述，在应变软化塑性体中应用扩容角ψ>0°的非关联流动法则可实现塑性扩容，那么在黏塑性体中应用相似的流动法则可实现流变扩容。
综上，适用于深部回采巷道分析的黏弹塑性本构模型应由图3所示元件串联组成(图3中，K为体积模量；GH为胡克体剪切模量，即剪切模量；ηN为受限牛顿体黏度；GK为凯尔文体剪切模量；c∞为长期黏聚力；c为黏聚力；ηK为凯尔文体黏度；ηV为改进黏塑性体黏度)。
图3 BVS模型元件组成(红色代表改进的元件)
Fig.3 Components of BVS model (red represents improved components)
该模型可视为由改进伯格斯(Burgers)体、改进黏塑性(viscoplastic)体和应变软化(strain softening)塑性体串联组成，下文简称BVS模型。
1.3 BVS模型本构方程
黏塑性体和应变软化塑性体均涉及路径依赖性，因此BVS模型采用增量形式的本构方程。增量本构方程目标是根据已知应力张量
和已知应变增量张量Δεij，输出新应力张量
其中i = x、y、z；j = x、y、z。对于黏弹塑性模型，可先假设输入的应变增量Δεij为黏弹性的，由此计算应力增量，结合输入的应力张量
得到假想黏弹性应力张量
之后经黏塑性与瞬时塑性修正输出新应力张量
应用增量塑性流动理论和流变理论[20,31]，可分别导出BVS模型假想黏弹性应力计算式、黏塑性应力修正式和瞬时塑性应力修正式(此处仅列出剪切屈服修正式)。
1.3.1 假想黏弹性应力
假想黏弹性应力计算式：
(1)
(2)
(3)
(4)
(5)
(6)
(7)
式中，
为假想黏弹性球应力；
为输入的球应力；Δεm为球应变增量；
为假想黏弹性偏应力；X、Y、A和B均为组合参量；Δeij为偏应变增量；
为输入的偏应力；
为输入的凯尔文体偏应变；Δt为时间步长；δij为Kroenecker delta符号，i=j时δij=1，其余情况为0。
1.3.2 黏塑性应力修正
对假想黏弹性应力张量
求特征值，可得到假想黏弹性主应力
将长期强度对应的黏聚力和屈服函数分别定义为长期黏聚力c∞和长期屈服函数f∞，则
(8)
(9)
(10)
式中，Nφ和Nψ分别为内摩擦角φ和扩容角ψ的函数。
若假想黏弹性主应力
使f∞>0，则需根据式(11)进行黏塑性应力修正：
(11)
式中，
为黏塑性应力修正后的主应力
为改进黏塑性体球应变增量；
为改进黏塑性体偏应变增量(主应力空间)。
1.3.3 瞬时塑性应力修正
瞬时塑性应力修正用到的屈服函数f为
(12)
式中，c为黏聚力。
若黏塑性应力修正后的主应力
使f >0，则需根据式(13)～(15)进行瞬时塑性应力修正：
(13)
(14)
(15)
(16)
(17)
式中，
和
分别为瞬时塑性修正后的最大、中间和最小主应力；
和
分别为黏塑性修正后的最大、中间和最小主应力；λs为一致性条件确定的循环内常量；α和β均为组合参量。
将瞬时塑性应力修正后的主应力变换回参考系，即可输出新的应力张量
达到三维增量本构方程的目标。
1.4 BVS模型力学特性实现
1.4.1 应变软化与塑性扩容
文献[32]通过数据挖掘，在沉积岩大量三轴试验数据基础上，同时给出应变软化强度参数退化模型和扩容角模型。此外，基于岩石微观力学观点，指出随着软化参量κ增大，M-C强度参数中仅黏聚力c发生退化，而内摩擦角φ保持恒定。
其中，黏聚力c为软化参量κ的函数：
(18)
式中，c0为初始黏聚力，MPa；ac为取决于岩性的拟合参数。
扩容角ψ为围压σ3和软化参量κ的函数：
(19)
(20)
式中，ψ0为初始扩容角，(°)；σc为单轴抗压强度，MPa；aψ、Aψ和Bψ均为取决于岩性的拟合参数。
文献[32]中软化参量κ采用塑性剪应变形式：
(21)
式中，Δκ为软化参量增量；ΔγS为塑性剪应变增量；
和
分别为剪切屈服时的最大和最小塑性主应变。
在瞬时塑性应力修正后计算κ，并根据式(18)更新黏聚力c，根据式(19)和(20)更新扩容角ψ，即可实现符合试验规律的应变软化和塑性扩容。
此外，应变软化后的岩体有着更低的长期强度[28]，在未发生应变软化的情况下，即软化参量为0时，岩样长期强度低于瞬时强度，设初始长期黏聚力c∞0与初始黏聚力c0之比为kc。岩样内部裂纹充分萌生与扩展并进入残余阶段后，应变软化和流变损伤均已停止，此时残余长期黏聚力c∞r与残余黏聚力cr相等。假设岩样自应变软化开始到进入残余阶段(对应残余软化参量κr)的过程中，长期黏聚力c∞与黏聚力c比值是线性变化的(在下文校核中可验证这一假设的合理性)，即：
(22)
根据式(18)和(22)，可在发生应变软化的情况下更新长期黏聚力c∞，实现长期强度降低。
1.4.2 加速蠕变、流变损伤与流变扩容
流变损伤与应变软化均由岩体塑性变形过程中裂纹萌生与扩展引起。应变软化以应变软化塑性体的剪应变γS作为软化参量，因此流变损伤可以改进黏塑性体的剪应变γV作为损伤参量。γV可取与γS相似的增量形式：
(23)
式中，
和
分别为最大和最小黏塑性主应变。
如前所述，当黏塑性剪应变γV超过某一阈值
后岩体强度才开始降低，对应减速和等速蠕变阶段累计的黏塑性剪应变。
巷道围岩随时间变形过程中应力不断调整，属流变现象，蠕变3阶段往往不会连续发生；而在迭代时间步长内应力恒定，可视为短暂蠕变。若某一迭代时间步长内应力水平高于长期强度，则认为该迭代时间步长内发生了流变损伤，γV增大。当γV超过时，加速蠕变启动，岩体强度开始降低，即黏聚力c和长期黏聚力c∞开始减小。c和c∞均为软化参量κ的函数，因此需要将ΔγV按一定规则换算为软化参量增量Δκ，进而更新c和c∞。
(24)
式中，kγ为
时软化参量增量Δκ与黏塑性剪应变增量ΔγV之比。
长期黏聚力减小导致的长期强度降低可以使改进黏塑性体过应力[33]升高，进而使蠕变速率升高，但还不足以达到试验中加速蠕变的程度。因此在加速蠕变启动后还需减小改进黏塑性体黏度ηV。此处借鉴文献[24]提出的ηV变化规律(损伤参量定义与之不同)：
(25)
式中，
和
分别为改进黏塑性体初始黏度与蠕变失稳时刻的黏度；kη和aη均为拟合参数；κf为蠕变失稳时的软化参量。
流变扩容的实现与塑性扩容相似。在黏塑性应力修正后根据式(19)和(20)更新扩容角ψ，即可实现符合试验规律的流变扩容。
1.4.3 稳定蠕变上限
荷载低于长期强度情况下，岩体发生稳定蠕变，BVS模型中改进黏塑性体和应变软化塑性体均无响应，退化为图4所示的改进伯格斯模型。
图4 BVS模型退化为改进伯格斯模型
Fig.4 BVS model degenerates to improved Burgers model
模型中加入自由牛顿体是为描述一些岩样在荷载低于长期强度情况下仍出现长时间等速蠕变的现象，比如口孜东矿岩样[34]。但这样做会引起2个问题：一是非静水压地应力难以维持：在初始平衡计算过程中，采用位移边界条件时地应力会逐渐松弛至静水压地应力，而采用应力边界条件时模型将持续变形无法收敛；二是巷道开挖后，应力水平较低，本该趋于稳定的深层围岩会持续变形，即稳定蠕变无法实现。因此，根据蠕变终止曲线理论导出对模型中自由牛顿体的限制条件，以解决这2个问题。
如图5所示，σct为蠕变启动应力；σc1、σc2和σc3为依次增大的蠕变应力；σ∞和σc分别为长期强度和单轴抗压强度。当蠕变应力低于长期强度时，发生稳定蠕变，蠕变变形随时间趋于极限。将低于长期强度的蠕变应力对应的蠕变终点连接可得蠕变终止曲线，其形态近似直线[35]。因蠕变启动应力较低，比如文献[36]中红砂岩蠕变启动应力仅12% σc，忽略蠕变启动应力只会引起较小的误差。为简化本构方程，BVS模型采用直线形式、不考虑蠕变启动应力的蠕变终止曲线。
图5 蠕变启动应力对蠕变终止曲线的影响
Fig.5 Effect of initiation stress on creep termination curves
如图6所示，E和Ef分别为弹性模量和峰后变形模量[37]；Ec为蠕变终止曲线斜率；kσ为长期强度σ∞与单轴抗压强度σc之比。岩样加载至σc1的过程中产生瞬时弹性变形εe，在σc1的持续作用下，岩样发生蠕变变形并趋于上限εc。则
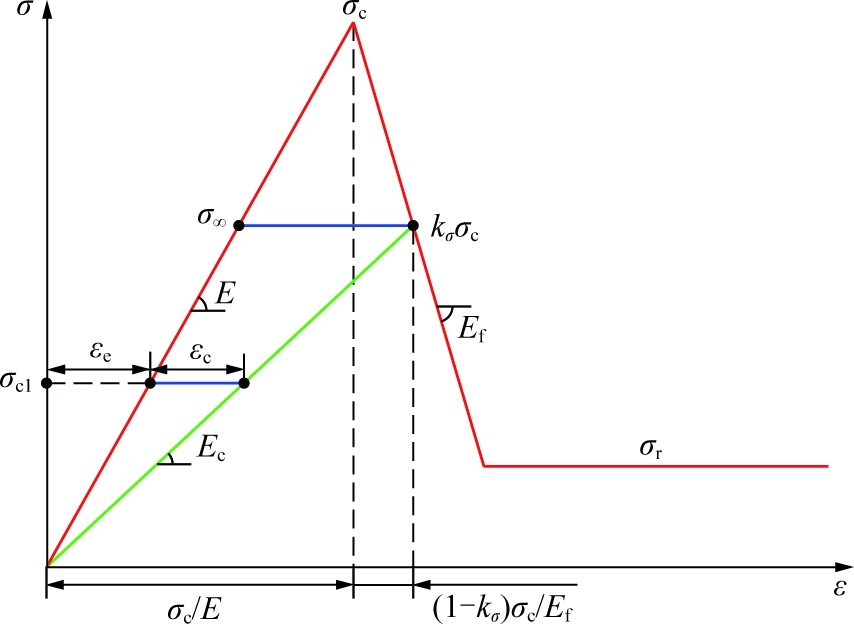
图6 蠕变终止曲线斜率与稳定蠕变上限
Fig.6 Slope of creep termination curve and upper bound of steady creep
(26)
(27)
为在BVS模型中应用，需将式(27)改写为偏应力-偏应变的形式。由图4可知，εc由受限牛顿体和凯尔文体产生，这两者均无球应力-球应变响应，即球应变恒为0。此外，单轴压缩条件下σ2和σ3均为0，根据偏应力和偏应变定义，可以得到最大偏应力s1和最大偏应变极限值
(受限牛顿体和凯尔文体最大偏应变之和)分别与蠕变应力σc1和稳定蠕变上限εc的对应关系：
(28)
(29)
将式(28)和(29)代入式(27)，可以得到用表示的稳定蠕变上限：
(30)
达到蠕变上限需要很长的时间，而凯尔文体在减速蠕变阶段结束时达到其变形上限，因此可以用减去凯尔文体最大偏应变极限值
得到受限牛顿体最大偏应变极限值
表示的稳定蠕变上限：
(31)
应力水平低于长期强度情况下，若受限牛顿体最大偏应变
则将受限牛顿体黏度ηN暂时设为无穷大以关闭受限牛顿体，进而实现稳定蠕变。若在之后的计算中应力水平升高使增大或应力水平高于长期强度，则暂时将ηN设定回初值以打开受限牛顿体；若应力水平达到瞬时强度，即进入峰后阶段，此时蠕变已不稳定[38]，则ηN恒为初值，受限牛顿体恒开。
1.5 BVS模型计算流程与数值实现
采用C++将BVS模型编写为可供FLAC3D调用的数值形式，其主要计算流程如图7所示。此外，为应变软化、动态扩容角和蠕变终止曲线限制等分别设置开关，在本构模型调用时可分别考虑、同时考虑或均不考虑这些力学特性，以便校核模型和分析这些力学特性的影响。
图7 BVS模型计算流程
Fig.7 Process of BVS model
2 BVS模型参数辨识与校核
2.1 参数辨识
BVS模型共有19个输入参数，见表1。其中参数1～5可由常规岩石力学试验得出；参数6～9为引入应变软化和扩容角模型所涉及拟合参数，文献[32]在大量沉积岩试验数据基础上已给出；参数10～18可由分级加载蠕变曲线得到；参数19由式(26)计算得出。
表1 BVS模型参数
Table 1 Parameters of BVS model
编号参数参数含义辨识结果1K/GPa体积模量11.2282GH/GPa虎克体剪切模量,即剪切模量11.4293φ/(°)内摩擦角254c0/MPa黏聚力初值11.9455σT/MPa抗拉强度3.736ac与黏聚力c有关的拟合参数,详见式(18)0.327aψ与扩容角ψ有关的拟合参数,详见式(19)0.128Aψ与扩容角ψ有关的拟合参数,详见式(20)6.2869Bψ与扩容角ψ有关的拟合参数,详见式(20)16.74410ηN0/(GPa·h)受限牛顿体黏度初值3 379.311ηK/(GPa·h)凯尔文体黏度23.12812GK/GPa凯尔文体剪切模量32.28013ηV0/(GPa·h)改进黏塑性体黏度初值6 630.614c∞0/MPa长期黏聚力初值8.36215aη与改进黏塑性体黏度ηV有关的拟合参数,详见式(25)0.0116kη与改进黏塑性体黏度ηV有关的拟合参数,详见式(25)0.98217kγ软化参量增量与黏塑性剪应变增量之比11.09218γV0/10-5加速蠕变启动的黏塑性剪应变阈值4.27119Ec/GPa蠕变终止曲线斜率15.36
2.1.1 弹塑性参数辨识
采用文献[34]中口孜东矿岩石力学试验数据进行参数辨识。以泥质砂岩为例，其弹性模量E为25.60 GPa，泊松比为0.12，单轴抗压强度σc为37.50 MPa，对应体积模量K为11.228 GPa，胡克体剪切模量GH为11.429 GPa，内摩擦角φ为25°，黏聚力初值c0为11.945 MPa；抗拉强度σT为3.73 MPa。文献[32]给出了泥质砂岩应变软化与扩容相关的拟合参数ac = 0.32，aψ = 0.12，Aψ = 6.268，Bψ = 16.744。
2.1.2 减速与等速蠕变参数辨识
文献[34]采用等时曲线方法确定口孜东矿泥质砂岩长期强度与单轴抗压强度σc之比在0.6～0.7，本文取0.7，即26.25 MPa，对应长期黏聚力初值c∞0为8.362 MPa。
对于荷载低于长期强度的情况，根据本构方程式(1)～(7)，并应用Boltzmann线性叠加原理，可导出分级加载条件下BVS模型各级蠕变应力的一维蠕变方程(不含瞬时应变项)：
(32)
式中，εcn(t)为第n级蠕变应力下蠕变量随时间t的变化规律；σn为第n级蠕变应力；Δσn为第n级蠕变应力增量。
对于荷载高于长期强度但加速蠕变尚未启动的情况，可由式(33)和(34)表示的黏塑性体流动法则导出黏塑性最大主应变增量
(33)
(34)
(35)
式中，g∞为长期塑性势函数；
为黏塑性主应变增量(k = 1，2，3);<f∞>为f∞的开关函数，f∞>0时<f∞>=f∞，其余情况为0。
对时间求导后与式(32)叠加得到该条件下的一维蠕变方程(不含瞬时应变项)：
(36)
文献[34]对7号砂质泥岩进行了蠕变应力0.4～0.9 σc、增量0.1σc的分级蠕变加载试验。考虑到加载至第1级蠕变应力用时久而减速蠕变持续时间短，该级曲线不用作参数辨识。如图8所示，采用式(32)和(36)分别对第2～4级(0.5～0.7 σc，荷载低于长期强度)和第5级蠕变应力(0.8σc，荷载高于长期强度但加速蠕变尚未启动)对应的蠕变曲线进行拟合，得到受限牛顿体黏度初值
凯尔文体剪切模量GK= 32.280 GPa，凯尔文体黏度ηK= 23.128 GPa·h，改进黏塑性体黏度初值
图8 减速与等速蠕变曲线拟合结果
Fig.8 Fitting results of deceleration and constant creep curves
此外，蠕变终止曲线斜率Ec由式(26)给出，其中峰后变形模量Ef根据文献[34]中试验曲线估计为弹性模量E的1.8倍，则蠕变终止曲线斜率Ec=15.36 GPa。
2.1.3 加速蠕变参数辨识
加速蠕变启动后，黏聚力c、长期黏聚力c∞和改进黏塑性体黏度ηV均随黏塑性剪应变γV增大而减小。式(36)不能反映这些参数的变化，其曲线偏离试验曲线的点即为加速蠕变起点，与加速蠕变曲线之差再加上式(36)第2项即为黏塑性最大主应变
的变化规律，如图9所示。由图9可知，第5级蠕变应力30.00 MPa持续了24 h，破坏级蠕变应力33.75 MPa在加速蠕变启动前持续了1.194 h，根据式(23)、(33)和(34)计算得到黏塑性剪应变阈值
4.271×10-5。
图9 破坏级应力蠕变曲线与黏塑性最大主应变
Fig.9 Creep curves under failure-level stress and viscoplastic maximum principal strain
黏塑性体最大主应变在蠕变失稳时刻达到4.692×10-5(仅加速蠕变阶段)，根据式(23)、(33)和(34)可计算得到加速蠕变阶段黏塑性剪应变增量ΔγV= 2.609×10-4。岩样瞬时强度在蠕变失稳时刻刚好降低至无法承受破坏级应力0.9 σc，则蠕变失稳时刻黏聚力为0.9c0(无围压条件下)，代入式(18)解得蠕变失稳时刻软化参量κf= 2.894×10-3。
考虑到加速蠕变阶段软化参量增量Δκ=κf，由Δκ/ΔγV可得软化参量增量与黏塑性剪应变增量之比kγ= 11.092。自加速蠕变起点，对图9中黏塑性最大主应变数据拟合可得
(37)
将式(37)代入式(23)(由式(33)和(34)可知与
之比恒为-1/Nψ)并乘以kγ可得软化参量κ随时间的变化规律：
κ=0.000 873 8t1.571
(38)
将式(18)和(22)表示的长期黏聚力c∞代入式(18)得到长期屈服函数f∞的变化规律，将f∞和式(25)代入式(35)，积分后可得黏塑性最大主应变在加速蠕变阶段的表达式(39)。考虑到黏聚力c由c0下降至0.9c0的过程中近似线性减小的特点且
并将式(38)代入式(39)可得在加速蠕变阶段的近似表达式(40)。
(39)
(40)
将已知参数代入式(40)，选取多组aη和kη计算得到随时间变化的曲线，如图10所示。当aη=0.01，kη=0.892时，式(40)和(37)曲线相似度最高。至此，BVS模型所有参数辨识完毕，汇总见表1。
图10 黏塑性最大主应变曲线
Fig.10 Curves of viscoplastic maximum principal strain
2.2 校 核
首先，BVS模型由多个元件串联而成，应能单独描述每一个元件的应力-应变响应；其次，应能描述图1所示的每一种力学特性，即参数变化和应力-应变响应符合预期规律；最后，采用与试验相同的加载方式，蠕变曲线应与试验曲线一致。校核用参数取自表1。
2.2.1 单一元件校核
通过设定受限牛顿体黏度ηN、凯尔文体黏度ηK、长期黏聚力c∞和黏聚力c为无穷大可分别关闭BVS模型中受限牛顿体、凯尔文体、改进黏塑性体和应变软化塑性体，利用这一特性进行单一元件校核。本小节不考虑图1所示力学特性。
参照文献[30]中Oedometer test方法，建立图11所示单一网格数值模型，将所得结果与理论解对比以校核模型。对单轴恒载和位移侧限恒载两种情况进行计算，校核包含胡克体的受限牛顿体、凯尔文体和改进黏塑性体；采用位移控制加载，对单轴加载和位移侧限加载2种情况进行计算，校核包含胡克体的应变软化塑性体。
图11 单一网格数值模型
Fig.11 Single-grid numerical model
各元件理论解可由增量塑性流动理论和流变理论[20,31]导出，在此不单独列出。受限牛顿体、凯尔文体、改进黏塑性体和应变软化塑性体的校核结果分别如图12～15所示(前3个校核略去瞬时弹性应变)，各元件数值计算结果均与理论解精确吻合。
图12 受限牛顿体校核结果(按牛顿体考虑)
Fig.12 Validation results of constrained Newtonian body (Considered as Newtonian body)
图13 凯尔文体校核结果
Fig.13 Validation results of Kelvin body
图14 改进黏塑性体校核结果(按理想黏塑性体考虑)
Fig.14 Validation results of improved viscoplastic body(Considered as ideal viscoplastic body)
图15 应变软化塑性体校核结果(按理想塑性体考虑)
Fig.15 Validation results of strain softening plastic body(Considered as ideal plastic body)
2.2.2 力学特性校核
由图1可知，BVS模型涉及深部巷道围岩6个力学特性：应变软化、塑性扩容、流变扩容、稳定与非稳定蠕变、蠕变3阶段和流变损伤。其中，应变软化由黏聚力c的变化控制，校核应变软化即校核黏聚力c是否按式(18)描述的规律变化；塑性扩容、流变扩容主要由扩容角ψ控制，校核两者即校核扩容角ψ是否按式(19)描述的规律变化；对于稳定与非稳定蠕变校核，可分别进行低于和高于长期强度的单轴恒载计算，荷载低于长期强度应发生稳定蠕变，反之亦然；蠕变3阶段和流变损伤在非稳定蠕变时体现，无须单独校核，将在2.2.3节体现。
黏聚力c和扩容角ψ均与塑性剪应变有关，可在同一次计算中校核两者。考虑到巷道围岩扩容，以及切向(z)压缩、径向(x)膨胀和轴向(y)位移约束的特点，采用图16所示加载方式，此外，按埋深1 000 m静水压地应力25 MPa设定应力初值。
图16 黏聚力与扩容角校核加载方式
Fig.16 Loading method for validations of cohesion and dilation angle
将采用BVS模型计算得到的黏聚力c变化规律与式(18)和FLAC3D内置应变软化模型[30]对比，如图17(a)所示；将采用BVS模型计算得到的扩容角ψ变化规律与式(19)对比(FLAC3D内置应变软化模型无法考虑围压对ψ的影响，故不作对比)，如图17(b)所示。由图17可知，BVS模型可精确描述应变软化与扩容。
图17 黏聚力与扩容角变化规律校核结果
Fig.17 Validation results of variations of cohesion and dilation angle
稳定和非稳定蠕变采用图11(a)所示单轴恒载方式校核，蠕变应力分别设定为低于长期强度(0.7 σc)的0.13σc、0.40σc、0.67σc，和高于长期强度的0.80σc和0.93σc。如图18所示，蠕变应力低于长期强度情况下发生稳定蠕变，且蠕变上限随蠕变应力增大而升高；蠕变应力高于长期强度情况下发生非稳定蠕变，且蠕变失稳时间随蠕变应力增大而缩短，与前人在试验中得到的规律一致[25]。这表明BVS模型可精确判别稳定与非稳定蠕变，反映蠕变应力变化带来的影响，但对稳定蠕变曲线形态的描述欠佳。
图18 稳定与非稳定蠕变校核结果
Fig.18 Validation results of steady and unsteady creep
2.2.3 分级加载蠕变曲线校核
本节采用与文献[34]相同的分级加载方式对图11(a)所示的数值模型进行计算，将得到的结果与试验曲线和理论解对比。其中，理论解由式(37)、(38)和(40)给出，校核结果如图19所示。可以看出BVS模型计算结果与理论解精确吻合，与试验曲线一致。这表明BVS模型可描述分级加载条件下的蠕变3阶段和流变损伤特性。
图19 分级加载蠕变校核结果
Fig.19 Validation results of step loading creep
3 工程验证分析
3.1 工程概况
以中煤能源集团新集口孜东矿121302工作面运输巷为研究对象，分析深部软岩回采巷道围岩变形与破坏规律，并验证BVS模型的合理性与适用性。
121302工作面采掘布置如图20所示。121302工作面属于孤岛工作面，相邻121301、121303工作面采空区，开采煤层平均厚度为4.9 m。运输巷埋深1 000 m，煤柱宽度15 m。巷道断面为直墙半圆拱，沿顶板剥岩掘进，留底煤2～3 m。煤层顶底板以软弱泥岩和砂质泥岩为主。煤层、泥岩及细砂岩单轴抗压强度分别为10.1、37.7和91.0 MPa。实测的垂直应力、最大水平主应力和最小水平主应力分别为25.12、21.84和11.42 MPa。运输巷围岩详细地质条件见文献[19]。
图20 121302工作面采掘布置平面图
Fig.20 Layout of No.121302 working face
运输巷支护布置如图21所示，采用锚网索支护，有些地段还进行了喷浆与滞后注浆加固，支护参数详见文献[15]。采用该支护方案后，运输巷围岩发生大变形。掘进与回采期间累计起底10次，扩帮深度3 m以上，累计底臌量超过6 m，两帮收缩超过4 m。
图21 巷道断面与支护布置
Fig.21 Cross-section and support layout of the roadway
3.2 数值模型与模拟方案
根据对称性，选取121301和121302工作面半长位置作为模型宽度(x方向)边界，则x=121301工作面半长+煤柱宽度+121302运输巷宽度+121302工作面半长= 360.8 m；考虑现场监测数据范围，模型厚度(y方向)取300 m。根据煤层顶底板岩层分布，取模型高度(z方向)为180.3 m。为提高计算效率，对研究区域局部加密，采用BVS模型计算，其余区域网格较稀疏采用M-C模型计算，如图22所示。
图22 数值模型
Fig.22 Numerical model
按实测地应力赋值模型初始应力，考虑重力加速度g=9.81 m/s2及其引起的应力梯度。模型底部限制法向位移，顶部采用法向面力代替上覆岩重，侧面采用与初始应力匹配的正应力+剪应力边界条件。在模型初始平衡前，将BVS模型中受限牛顿体和凯尔文体应变张量初始化为与地应力相匹配的值，以考虑地层在地应力形成漫长地质时期内的蠕变量[25,30]。
根据煤岩样力学性质测试结果[19]，将强度参数折减约50%[39]，受限牛顿体黏度初值、凯尔文体黏度、凯尔文体剪切模量、改进黏塑性体黏度初值和蠕变终止曲线斜率根据蠕变曲线一致性理论[18,25,40]按围岩与表1岩样弹性模量之比估计，描述各岩性黏聚力和扩容角变化规律的拟合参数由文献[32]给出，其余描述煤岩固有性质的参数(如内摩擦角)保持不变，得到表2用于数值计算的参数，互层情况取两种岩性参数均值。数值模型中仅模拟锚杆与锚索支护。
在模型内采用Fish语言控制分步掘进与回采，每次掘进0.8 m并采用Cable结构单元安装锚杆(索)，利用刚性节点模拟托盘作用，采用Pretension关键字施加预应力；回采工作面距研究区域大于100 m时每次回采8 m，距研究区域不大于100 m时每次回采4 m，并采用低强度、低刚度弹塑性体(M-C模型)回填采空区以模拟垮落矸石的支撑作用。根据现场采掘记录，121302运输巷平均掘进速度约6.62 m/d，121301和121302工作面平均回采速度约3.81 m/d，在模型内每次掘进和回采后，除计算瞬时弹塑性平衡外，再进行相应时间流变计算，以考虑采掘速度影响。
模型主要开挖与计算步骤为：121301工作面回采→进行与现场一致为期1 a的流变计算→掘进121302运输巷→进行121302工作面回采前的流变计算→121302工作面回采。根据数值稳定性规则[30]，计算时间步长Δt不可超过
或ηK/GK，由表2可知，和ηK/GK最小值为0.72 h，故本次模拟取Δt = 0.1 h以保证良好的数值稳定性。
表2 数值模型参数
Table 2 Parameters in the numerical model
编号参数参数值13-1号煤泥岩砂质泥岩细砂岩1K/GPa1.5729.79311.66710.4022GH/GPa1.1795.8767.0009.1473φ/(°)232729344c0/MPa1.6685.7766.93612.1005σT/MPa0.8151.8651.9253.4356ac0.350.340.320.297aψ0.1300.1250.1200.1008Aψ5.7926.7946.2867.4869Bψ13.27015.30816.74428.35110ηN0/(GPa·h)425.02 506.62 628.23 186.911ηK/(GPa·h)2.90814.49517.26822.564
续表
参数编号参数参数值13-1号煤泥岩砂质泥岩细砂岩12GK/GPa4.06025.29230.13226.86513ηV0/(GPa·h)834.04 918.55 157.36 253.514c∞0/MPa1.1684.0434.8558.47015aη0.010.010.010.0116kη0.9820.9820.9820.98217kγ11.09211.09211.09211.09218γV0/10-54.2714.2714.2714.27119Ec1.69810.01410.50012.732
3.3 数值模拟结果分析
3.3.1 邻近工作面的影响
121301工作面停采1 a后、121302运输巷掘进前，未来煤柱宽度内煤体和底板泥岩在工作面侧向支承压力作用下已发生显著劣化，如图23所示。定义围岩强度劣化比kc =黏聚力c/峰值黏聚力c0，则kc <0.3的煤体距巷道煤柱帮仅5 m，更深处已进入kc≈0.1的残余区，这与现场煤柱帮窥视孔深6 m后钻进困难、窥视过程中塌孔的现象一致。
图23 邻近工作面停采1 a后围岩强度劣化比(c/c0)
Fig.23 Strength deterioration ratio (c/c0) of the surrounding rock 1 a after stopping of the adjacent working face
3.3.2 掘进的影响
如图24所示，超前掘进工作面3.2 m时，煤壁在侧向卸荷作用下已开始劣化，呈向掘进空间挤出趋势，位移量最大仅18 mm。巷道断面形成后、距掘进工作面5.6 m时，无论煤柱帮还是工作面帮煤体均显著劣化，且掘进引起的劣化区与邻近工作面引起的劣化区连接，巷道宽度内底板泥岩也开始发生劣化；底煤开始臌起，底臌量达318 mm。巷道断面距掘进工作面20.0 m时，围岩劣化区继续扩展，表现为顶板浅层明显劣化、工作面帮煤体和底板泥岩劣化区加深；虽然顶板浅层劣化，但顶板为锚固岩体且为拱顶结构，变形量微小，顶板下沉量仅38 mm；巷帮锚固煤体明显变形，移近量(单侧)约300 mm；无支护底煤显著变形，底板泥岩也因底煤劣化卸荷而向上鼓起、超出原煤岩分界面，共同导致底臌量达559 mm。
图24 掘进期间巷道围岩位移与劣化
Fig.24 Displacement and deterioration of the roadway surrounding rock during tunnelling
3.3.3 流变的影响
根据数值计算结果，巷道断面距掘进工作面>20 m后，掘进应力调整导致的影响大幅减弱，流变逐渐成为主导因素。如图25所示，巷道掘进后流变效应凸显、围岩大范围持续劣化，围岩变形呈顶板下沉量较小、肩窝三角煤扩容、巷帮锚固体整体内移和剧烈底臌的特点，与现场观测结果[7,19]一致。底煤持续扩容，底板泥岩持续臌起驱动底煤挤入巷道空间，导致巷道剧烈底臌。巷道断面形成20、60和180 d后底臌量分别达1 227、1 770和2 391 mm，0～20、20～60和60～180 d底臌增量分别为1 103(含掘巷影响)、543和621 mm。
图25 流变阶段巷道围岩位移与劣化
Fig.25 Displacement and deterioration of the roadway surrounding rock during rheology
3.3.4 回采的影响
如图26所示，工作面回采对巷道扰动强烈、超前支承压力导致围岩大范围劣化。巷道断面距回采工作面49.6 m时，回采扰动已较为显著；距回采工作面13.6 m时，顶板也发生明显变形，顶板下沉量达239 mm；距回采工作面1.6 m时，回采巷道生命周期已近末尾，顶板下沉量、工作面帮移近量、煤柱帮移近量和底臌量分别达269、1 298、1 021和3 177 mm，底板泥岩向巷道断面内挤入，巷道断面接近闭合。
图26 回采期间巷道围岩位移与劣化
Fig.26 Displacement and deterioration of the roadway surrounding rock during stoping
3.3.5 监测数据分析
在顶底板和两帮中部设置测点监测围岩表面位移量，结果如图27所示。围岩表面位移量在掘进扰动期间快速增大，随后呈衰减-等速流变规律，200 d后仍缓慢变形；回采扰动距工作面100 m时已较明显，距工作面50 m后更为显著；底臌量>巷帮移近量>顶板下沉量。
图27 围岩表面位移量变化规律
Fig.27 Variation of surface displacements of the surrounding rock
因底板变形与破坏最为严重，在底板深度1.5 m处设置测点监测软化参量，结果如图28所示，其中流变直接导致的软化参量由改进黏塑性体产生，应力调整导致的软化参量由应变软化塑性体产生。底板深度1.5 m处软化参量已远大于残余强度对应值，但软化参量与围岩瞬时塑性和黏塑性剪应变以及扩容呈正相关，反映了底板剧烈扩容变形的情况；流变直接导致的软化参量占比较小，全程仅0～16%，但流变是引起应力调整的主要因素之一，特别是在非掘进和回采影响阶段，间接导致软化参量总体增大。
图28 底板软化参量变化规律
Fig.28 Variation of the softening parameter of the floor
3.3.6 数值模拟结果与井下实测数据对比分析
井下巷道变形曲线如图29所示，数值模拟结果与井下实测数据的对比见表3。
表3 巷道变形数值模拟与实测数据对比
Table 3 Roadway deformation comparison between numerical simulation and field monitoring data mm
阶段顶、底板移近量数值模拟井下实测两帮移近量数值模拟井下实测掘进与流变2 4932 3991 4591 275回采9534 3798603 529
图29 掘进、流变与回采阶段巷道变形曲线
Fig.29 Curves of roadway deformation in tunnelling,rheological and stoping periods
数值模拟结果表明：巷道在掘进、流变及回采影响阶段累计的顶底板、两帮移近量分别为3 446、2 319 mm，顶底板移近量中底臌量占92%。围岩变形主要由流变与回采影响引起。
井下实测数据表明：巷道掘进期间，顶底板、两帮移近量分别为2 399、1 275 mm；回采期间巷道顶底板、两帮移近量分别达4 379、3 529 mm；两阶段顶底板移近量中底臌量占85%以上。巷道掘进期间围岩变形就很大(其中已经包含了一部分流变变形)，回采影响期间围岩变形又剧烈增加，导致掘进与回采影响期间巷道累计顶底板、两帮移近量分别达6 778、4 804 mm。
数值模拟结果基本能够反映深部软岩扩容与流变的特性，然而，由于没有考虑现场多次起底与刷帮的二次扰动作用，数值模拟结果与实际情况还有较大差异(特别是修巷频繁的回采阶段)。今后还需要对围岩本构模型、数值模拟方法进行不断改进，以考虑更多影响深部软岩回采巷道变形与破坏的因素，使模拟计算结果更加接近实际。
4 结 论
(1)建立了可描述深部回采巷道围岩应变软化、塑性扩容、蠕变3阶段、稳定与非稳定蠕变、流变损伤和流变扩容的BVS模型。推导出该模型三维增量本构方程并将其开发为可供FLAC3D调用的数值形式。
(2)由BVS模型三维增量本构方程和中煤新集口孜东煤矿岩样试验数据辨识了模型的19个输入参数。采用试验数据、理论解和数值计算结果相互印证的方式进行校核，发现该模型可较好地描述深部软岩回采巷道围岩的6个力学特性。
(3)试验巷道数值模拟结果表明：围岩在掘进期间变形量较小；围岩在流变期间大范围持续劣化，呈顶板下沉量较小、肩窝三角煤扩容、巷帮锚固体整体内移和剧烈底臌的特点；回采对围岩扰动强烈，使其大范围劣化，巷道变形急剧增加。底板泥岩持续臌起驱动不断扩容的底煤挤入巷道空间是发生剧烈底臌的主要原因；底板深度1.5 m处流变直接导致的软化参量全程仅占比0～16%，但流变是引起应力调整的主要因素之一，间接导致软化参量总体增大。
(4)BVS模型对深部软岩回采巷道掘进、流变和回采阶段的围岩变形和破坏计算结果与井下实测数据所得规律基本一致。但数值模拟结果与实测数据还存在较大差异，还需要对本构模型、数值模拟方法进行不断改进，以考虑更多影响深部软岩回采巷道变形与破坏的因素，使数值模拟结果更加接近实际。
[1] 侯朝炯，王襄禹，柏建彪，等.深部巷道围岩稳定性控制的基本理论与技术研究[J].中国矿业大学学报，2021，50(1)：1-12.
HOU Chaojiong,WANG Xiangyu,BAI Jianbiao,et al.Basic theory and technology study of stability control for surrounding rock in deeproadway[J].Journal of China University of Mining and Technology，2021，50(1)：1-12.
[2] 康红普.我国煤矿巷道围岩控制技术发展70年及展望[J].岩石力学与工程学报,2021,40(1):1-30.
KANG Hongpu.Seventy years development and prospects of strata control technologies for coal mine roadways in China[J].Chinese Journal of Rock Mechanics and Engineering,2021,40(1):1-30.
[3] 康红普,王国法,姜鹏飞,等.煤矿千米深井围岩控制及智能开采技术构想[J].煤炭学报,2018,43(7):1789-1800.
KANG Hongpu,WANG Guofa,JIANG Pengfei,et al.Conception for strata control and intelligent mining technology in deep coal mines withdepth more than 1 000 m[J].Journal of China Coal Society,2018,43(7):1789-1800.
[4] LIN P,LIU H,ZHOU W.Experimental study on failure behaviour of deep tunnels under high in-situ stresses[J].Tunnelling &Underground Space Technology,2015,46:28-45.
[5] YI K,KANG H,JU W,et al.Synergistic effect of strain softening and dilatancy in deep tunnel analysis[J].Tunnelling &Underground Space Technology,2020,97:103280.
[6] 谢和平,高峰,鞠杨,等.深部开采的定量界定与分析[J].煤炭学报,2015,40(1):1-10.
XIE Heping,GAO Feng,JU Yang,et al.Quantitative definition and investigation of deep mining[J].Journal of China Coal Society,2015,40(1):1-10.
[7] 程利兴,康红普,姜鹏飞,等.深井沿空掘巷围岩变形破坏特征及控制技术研究[J].采矿与安全工程学报,2021,38(2):227-236.
CHENG Lixing,KANG Hongpu,JIANG Pengfei,et al.Deformation and failure characteristics and control technology of surrounding rocks in deeply gob-side entry driving[J].Journal of Mining &Safety Engineering,2021,38(2):227-236.
[8] 翁明月.深部大断面回采巷道顶板锚固层稳定控制机理与技术研究[D].阜新:辽宁工程技术大学,2017.
WENG Mingyue.controlling mechanism and technology for anchoring layer stability of roof in deep large section roadway[D].Fuxin:Liaoning Technical University,2017.
[9] 张海洋.云驾岭矿深部回采巷道围岩稳定性评价及支护技术研究[D].北京:中国矿业大学(北京),2017.
ZHANG Haiyang.The study on surrounding rock stability evaluation and its supporting technology of gateway in deep Yunheling coal mine[D].Beijing:China University of Mining and Technology-Beijing,2017.
[10] BRIDGMAN P.Volume changes in the plastic stages of simple
compression[J].Journal of Applied Physics,1949,20:1241-1251.
[11] 陈宗基，康文法.岩石的封闭应力、蠕变和扩容及本构方程[J].岩石力学与工程学报，1991，10(4)：299-312.
TAN Tiongkie,KANG Wenfa.On the locked in stress,creep and dilatation of rocks and the constitutive equations[J].Chinese Journal of Rock Mechanics and Engineering,1991,10(4):299-312.
[12] ALEJANO L R,ALONSO E.Considerations of the dilatancy angle in rocks and rock masses[J].International Journal of Rock Mechanics And Mining Sciences,2005,42:481-507.
[13] ZHAO X G,CAI M.A mobilized dilation angle model for rocks[J].International Journal of Rock Mechanics And Mining Sciences,2010,47:368-384.
[14] 康红普，王金华，林健.高预应力强力支护系统及其在深部巷道中的应用[J].煤炭学报，2007，32(12)：1233-1238.
KANG Hongpu,WANG Jinhua,LIN Jian.High pretensioned stress and intensive bolting system and its application in deep roadways [J].Journal of China Coal Society,2007,32(12):1233-1238.
[15] 康红普.深部煤矿应力分布特征及巷道围岩控制技术[J].煤炭科学技术,2013,41(9):12-17.
KANG Hongpu.Stress distribution characteristics and strata control technology for roadways in deep coal mines[J].Coal Science and Technology,2013,41(9):12-17.
[16] 孙钧.岩石流变力学及其工程应用研究的若干进展[J].岩石力学与工程学报,2007,26(6):1081-1106.
SUN Jun.Rock rheological mechanics and its advance in engineering applications[J].Chinese Journal of Rock Mechanics and Engineering,2007,26(6):1081-1106.
[17] 宗义江.深部破裂围岩蠕变力学特性与本构模型研究[D].徐州:中国矿业大学,2013.
SONG Yijiang.Study on creep mechanical properties and constitutive model of deep cracked surrounding rock [D].Xuzhou:China University of Mining and Technology,2013.
[18] 徐鹏.深部复合岩层流变力学行为及其对TBM卡机灾害影响机理研究[D].徐州:中国矿业大学,2018.
XU Peng.Study on rheological behavior of deep buried composite rock and its influencing mechanism on TBM Jamming disaster[D].Xuzhou:China University of Mining and Technology,2018.
[19] 康红普,姜鹏飞,黄炳香,等.煤矿千米深井巷道围岩支护-改性-卸压协同控制技术[J].煤炭学报,2020,45(3):845-864.
KANG Hongpu,JIANG Pengfei,HUANG Bingxiang,et al.Roadway strata control technology by means of bolting-modi-fication-destressing in synergy in 1 000 m deep coal mines[J].Journal of China Coal Society,2020,45(3):845-864.
[20] VERMEER P A.Non-associated plasticity for soils,concrete and rock[M].Dordrecht:Springer Netherlands,1998:163-196.
[21] YI K,LIU Z,LU Z,et al.Transfer and dissipation of strain energy in surrounding rock of deep roadway considering strain softening and dilatancy[J].Energy Science &Engineering,2021,9:27-39.
[22] YI K,LIU Z,LU Z,et al.Effect of axial in-situ stress in deep tun-
nel analysis considering strain softening and dilatancy[J].Energies，2020，13:1502.
[23] 赵延林,马文豪,唐劲舟,等.基于塑性扩张的岩石变参数蠕变损伤模型与工程应用[J].煤炭学报,2016,41(12):2951-2959.
ZHAO Yanlin,MA Wenhao,TANG Jinzhou,et al.Rock creep damage model with varying parameters based on plastic expansion and engi-neering application[J].Journal of China Coal Society,2016,41(12):2951-2959.
[24] 金俊超,佘成学,尚朋阳.基于应变软化指标的岩石非线性蠕变模型[J].岩土力学,2019,40(6):2239-2246.
JIN Junchao,SHE Chengxue,SHANG Pengyang.A nonlinear creep model of rock based on the strain softening index[J].Rock and Soil Mechanics,2019,40(6):2239-2246.
[25] 蔡美峰.岩石力学与工程[M].北京:科学出版社,2013.
[26] 杨圣奇,徐鹏.一种新的岩石非线性流变损伤模型研究[J].岩土工程学报,2014,36(10):1846-1854.
YANG Shengqi,XU Peng.A new nonlinear rheological damage model for rock[J].Chinese Journal of Geotechnical Engineering,2014,36(10):1846-1854.
[27] HU B,YANG S,XU P.A nonlinear rheological damage model of hard rock[J].Journal of Central South University,2018,25:1665-1677.
[28] 郭臣业,鲜学福,姜永东,等.破裂砂岩蠕变试验研究[J].岩石力学与工程学报,2010,29(5):990-995.
GUO Chenye,XIAN Xuefu,JIANG Yongdong,et al.Experimental research on creep of fractured sandstone[J].Chinese Journal of Rock Mechanics and Engineering,2010,29(5):990-995.
[29] 赵延林,唐劲舟,付成成,等.岩石黏弹塑性应变分离的流变试验与蠕变损伤模型[J].岩石力学与工程学报,2016,35(7):1297-1308.
ZHAO Yanlin,TANG Jinzhou,FU Chengcheng,et al.Rheological test of separation between viscoelastic-plastic strains and creep damage model[J].Chinese Journal of Rock Mechanics and Engineering,2016,35(7):1297-1308.
[30] ITASCAINC.FLAC3D:Fast lagrangian analysis of continua in 3 dimension.version 5.01[Z].Minneapolis,2012.
[31] 孙钧.岩土材料流变及其工程应用[M].北京:中国建筑工业出版社,1999.
[32] POURHOSSEINI O,SHABANIMASHCOOL M.Development of an elasto-plastic constitutive model for intact rocks[J].International Journal of Rock Mechanics &Mining Sciences,2014,66:1-12.
[33] 张树光,刘文博,陈雷,等.基于力学参数时效性的非定常蠕变模型[J].中国矿业大学学报,2019,48(5):993-1002.
ZHANG Shuguang,LIU Wenbo,CHEN Lei,et al.Unsteady creep model based on timeliness of mechanical parameters[J].Journal of China University of Mining &Technology,2019,48(5):993-1002.
[34] 陈伟强.基于微细观力学的砂质泥岩蠕变破坏机理研究[D].徐州:中国矿业大学,2019.
CHEN Weiqiang.Study on the creep failure mechanism of sandy
mudstone based on micro-mesoscopic mechanics[D].Xuzhou:China University of Mining and Technology,2019.
[35] 经纬.圆形巷道围岩变形分区的理论与试验研究[D].淮南:安徽理工大学,2017.
JING Wei.Theoretical and experimental research on deformation partition of axisymmetric circular roadway (tunnel)[J].Huainan:Anhui University of Science and Technology,2017.
[36] 夏才初,王晓东,许崇帮,等.用统一流变力学模型理论辨识流变模型的方法和实例[J].岩石力学与工程学报,2008,27(8):1594-1600.
XIA Caichu,WANG Xiaodong,XU Chongbang,et al.Method to identify rheological models by unified rheological model theory and case study[J].Chinese Journal of Rock Mechanics and Engineering,2008,27(8):1594-1600.
[37] BUKOWSKA M.Post-peak failure modulus in problems of mining geo-mechanics[J].Journal of Mining Science,2013,49:731-740.
[38] PENG S S.Time-dependent aspects of rock behavior as measured by a servocontrolled hydraulic testing machine[J].International Journal of Rock Mechanics &Mining Sciences &Geomechanics Abstracts,1973,10:235-246.
[39] 高富强.数值模拟在地下煤矿开采岩石力学问题中的应用[J].采矿与岩层控制工程学报,2019,1(1):21-28.
GAO Fuqiang.Use of numerical modeling for analyzing rock mechanicproblems in underground coal mine practices[J].Journal of Mining and Strata Control Engineering,2019,1(1):21-28.
[40] 牛双建,党元恒,冯文林,等.损伤破裂砂岩单轴蠕变特性试验研究[J].岩土力学,2016,37(5):1249-1258.
NIU Shuangjian,DANG Yuanheng,FENG Wenlin,et al.Uniaxial experimental study of creep properties of sandstone in damage and fracture states[J].Rock and Soil Mechanics,2016,37(5):1249-1258.
