Analysis of mining earthquakes mechanism based on structural dynamics theory
-
摘要:
矿震是地下煤层开采中较常见的动力学现象，揭示矿震的力学原理是其灾害评价、预测及防治的前提和基础，采用理论分析方法，探讨了矿震的力学原理与主控因子，研究了矿震中覆岩的下沉−振动响应特征，及其作用下覆岩应变能、重力势能和动能的演变机理。结果显示：在结构动力学视角下，矿震是一类典型的自由振动，由坚硬岩层破断等采场煤岩结构子系统的瞬时失稳触发，由采场煤岩结构瞬变后的初始状态驱动，不需要外部能量的输入，耗散采场煤岩自身的势能(重力势能+应变能)，受控于采场煤岩结构的力学性能与力学环境及其对应的瞬变特征。对于结构瞬变区域上方的覆岩，受坚硬岩层破断影响，覆岩载荷转递路径发生改变，采空区上方关键层上、下表面的承载量瞬时减小，采空区外侧关键层上表面的承载量瞬时增大。受此影响，关键层及其上覆岩层下沉−振动，其任意时刻的速度、位移和弯曲应变能线密度等响应特征均呈现出波动特性，且都以震源为中心迅速衰减。并且，在任意振动周期内，除了有能量的耗散外，亦存在不同能量间的相互转换；在第1个1/4周期内，重力势能向动能和应变能转换；在第2个1/4周期内，重力势能和动能向应变能转换；在第3个1/4周期内，应变能向重力势能和动能转换；在第4个1/4周期内，动能和应变能向重力势能转换。基于上述的理念，可以更直观地理解矿震中采场空间不同区域煤岩力学响应的发生机理及其内在关联等，为煤岩动力灾害的防控提供了新思路和新视角。
Abstract:Mine earthquake is a common dynamic phenomenon in underground coal seam mining, and revealing its mechanical mechanism is the premise and foundation for disaster evaluation, prediction, and prevention. In this paper, the theoretical analysis method is used to investigate the mechanical principles and main control factors of the mine earthquake, and to study the sinking-vibration response characteristics of the overlying rock in the mine earthquake, and the evolution mechanism of the strain energy, gravitational potential energy and kinetic energy of the overlying rock under the action. The results show that mine earthquake is a typical type of free vibration from the perspective of structural dynamics. The mine earthquake is induced by the instantaneous instability of the coal-rock structure subsystem such as the fracture of the hard rock layer. After the transient, it is driven by the initial state of the coal-rock structure of the stope, and does not require the input of external energy. Mine earthquake dissipates the potential energy (gravitational potential energy + strain energy) of coal and rock in the stope, which is controlled by the mechanical properties and mechanical environment of coal and rock structure in the stope and its corresponding transient characteristics. For the overlying strata above the structural transient area, under the influence of the hard rock layer breaking, the load transfer path of the overlying strata has changed, the bearing capacity of the upper and lower surfaces of the key stratum above the goaf decreases instantaneously, and the bearing capacity of the upper surface of the key stratum outside the goaf increases instantaneously. Affected by this, the key stratum and its overlying strata sink and vibrate, and the response characteristics such as velocity, displacement and bending strain energy linear density at any time show fluctuation characteristics, and decay rapidly with the focus of the mine earthquake as the center. Moreover, in any vibration period, there is energy dissipation and mutual conversion between different energies. In the first 1/4 period, the gravitational potential energy is converted to kinetic energy and strain energy. In the second 1/4 period, the gravitational potential energy and kinetic energy are converted to strain energy. In the third 1/4 period, the strain energy is converted to gravitational potential energy and kinetic energy. In the fourth 1/4 period, kinetic energy and strain energy are converted to gravitational potential energy. Based on the concept of this paper, the occurrence mechanism and internal correlation of coal-rock mechanical response in different areas of stope space during mine earthquake can be understood more intuitively, which provides new ideas and new perspectives for the prevention and control of coal-rock dynamic disasters.
-
0. 引 言
矿震是指矿山采掘活动诱发的非天然地震现象，是地下煤层开采中较常见的动力学现象[1]。并且，矿震的能量越大，越容易造成地下工程结构的瞬时失稳，诱发冲击地压、煤与瓦斯突出、突水等灾害[2-4]。因此，揭示矿震的力学原理，对煤岩动力灾害的防治具有重要意义。
近年来，众多学者通过理论分析、数值计算、模拟试验和现场实测等方法，对顶板运动型和断层错动型矿震的触发机理[5-8]、矿震中应力波的波形特征与衰减规律[9-11]、矿震动载扰动下煤岩动力灾害的发生机理[12-13]、矿震致灾预测评估机理[14-16]等问题展开了系统研究，并在此基础上，建立了矿井采掘优化布置、水力压裂与深孔爆破等煤岩动力灾害的区域防范与风险调控方法[17-19]。在某种程度上实现了“有震消灾”“有震减灾”“有震无灾”“无震无灾”的目的[20]，并为进一步的研究奠定了坚实基础。
然而，目前对矿震的认知多是基于地震的研究成果，沿用了地震中关于“震源”的释义，认为矿震中煤岩破裂、阻尼等耗散的能量与地震的情况类似，均来自于煤岩振动触发区域瞬时释放的应变能。但需注意的是，在地下煤层开采中，受煤体开挖影响，采空区是“空、虚的”，顶板垮落矸石的承载能力有限；在自重应力场作用下，坚硬岩层的瞬时破断或断层的瞬时活化，都势必会导致采空区上方覆岩的瞬时下沉、重力做功[21]。因此，在矿震研究中，重力势能的瞬时释放不应被忽略，但目前鲜见针对该问题的研究。
究其原因，目前对矿震的研究，主要聚焦于某一硬岩层或结构的瞬时失稳特征与应变能释放规律等，未将采动影响范围内的煤岩纳入到统一的力学系统中分析，未考虑矿震中不同煤岩层受载与力学响应的差异性。在实际工程中，受自重应力场和采动卸荷效应影响，采动影响范围内的各岩层相互作用、相互制约，存在紧密且复杂的力学联系，任意岩层的瞬时破断都会导致相邻岩层间作用关系的瞬变[22]。
据此，笔者在已有研究工作基础上，从结构动力学的理念和整个采场煤岩结构的视角出发，采用理论分析方法，探讨矿震的力学原理与主控因子，研究矿震中结构瞬变区域上方覆岩的下沉−振动响应特征，及其作用下覆岩应变能、重力势能和动能的演变机理，以期能为煤岩动力灾害的防治提供一定的理论支撑。
1. 矿震的力学原理浅析
以下基于结构动力学理论中力学系统、激励载荷和力学响应的内在联系，对照分析地下煤层开采中煤岩结构的瞬变特征及其触发的力学响应，探讨矿震的力学原理与主控因子。
1.1 基于激励载荷类型的振动分类
结构动力学理论是研究力学系统、激励载荷和力学响应三者关系的科学。这其中，力学响应受控于力学系统和激励载荷。按照输入的激励载荷类型，可将系统的动力学响应分为自由振动和强迫振动[23]。
1.1.1 自由振动
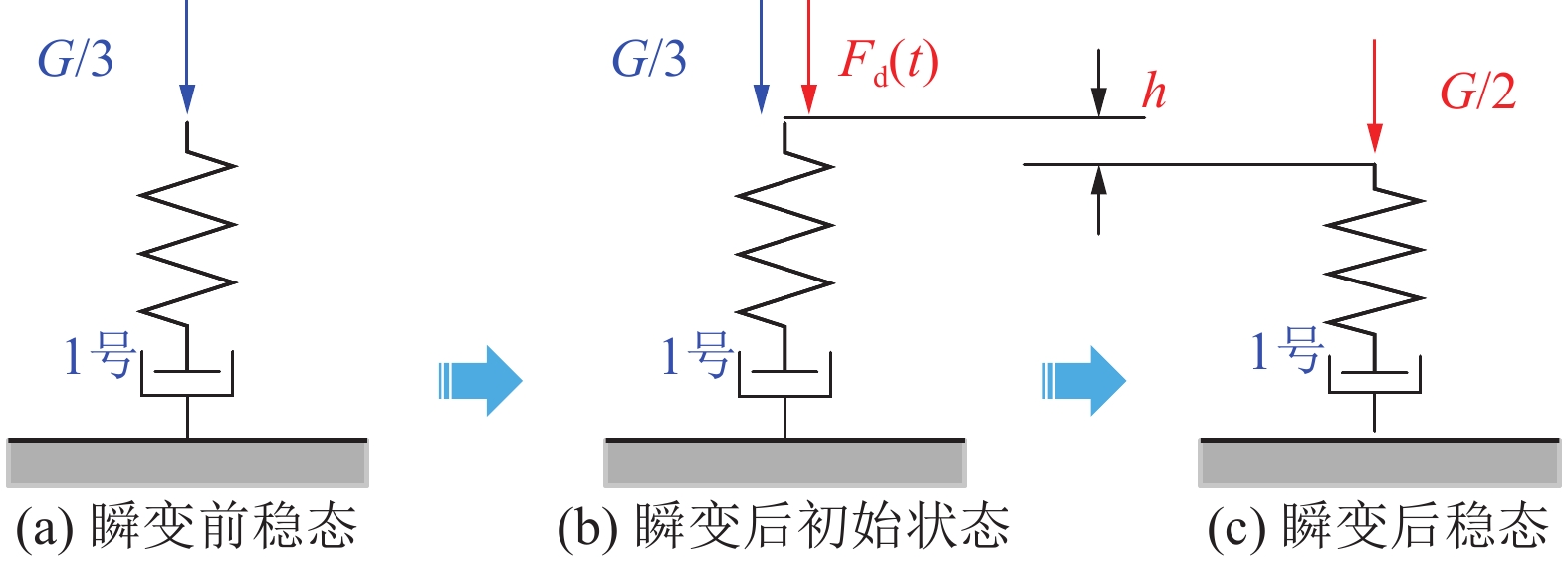
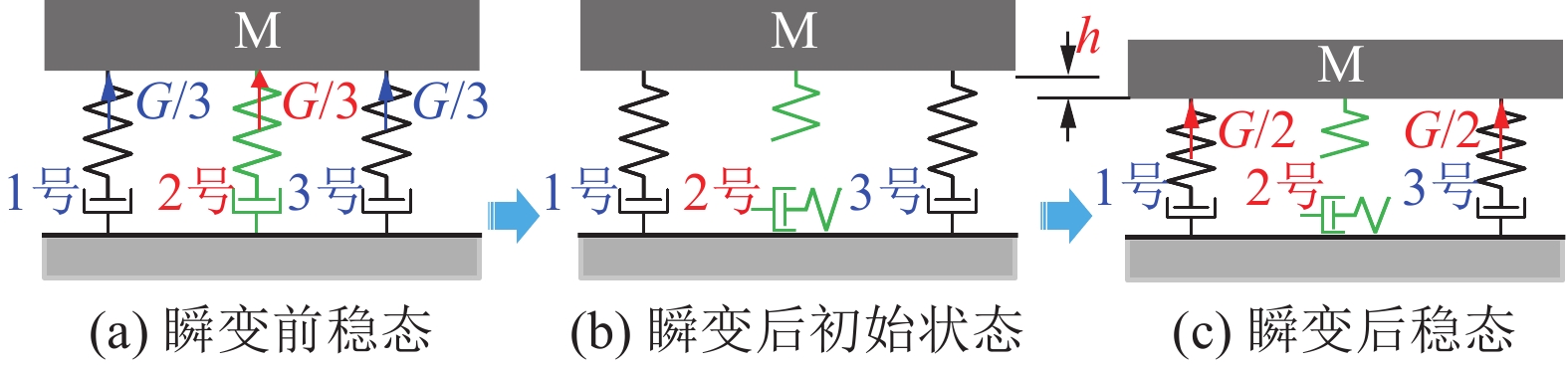
自由振动是指系统受到初始激励载荷后不再受激励载荷作用时产生的振动，其初始激励载荷一般为外部载荷的瞬时卸载。例如，在图1所示的系统中，当2号子系统瞬时破坏后，系统的结构发生了瞬变，等效于作用在2号子系统位置处、大小为G/3的载荷被瞬时卸载(激励载荷)，其中G为物块重力。系统将经历由稳态→非稳态→稳态的演变历程。
自由振动由系统的初始状态驱动，不需要外部能量的输入。对于单自由度系统，其动力学控制方程可表示为
J¨z(t)+c˙z(t)+kz(t)=0˙z(0)=˙z0, z(0)=z0 (1) 式中：J为质量，kg；z(t)为位移，m；t为时间，s；z0为初始位移，m；c为阻尼系数，(N·s)/m；k为弹簧刚度，N/m。式(1)中的初始速度和初始位移不能同时为0，其速度和位移以系统瞬变后的稳态为基准。
例如，图1所示的振动，由图1a中2号子系统的瞬时破坏(瞬时卸载)触发，由图1b所示系统结构瞬变后的初始状态驱动。在图1b所示的初始状态下，物块M的初始速度为0，初始位移为h，动力学过程中物块M释放Gh的重力势能，部分被耗散，部分转换为1号、3号子系统的弹性势能。并且，在此类振动中，由于初始的激励载荷来源于系统结构力学性能或力学环境的瞬变，因此从静力学的范畴看，振动前、后2个稳态时系统的静态力学响应会发生阶变[21, 24-25]。
1.1.2 强迫振动
强迫(受迫)振动是指系统在外部动载作用下产生的振动。例如，在图1中，从整个系统的角度看是自由振动，但任意子系统却是强迫振动，如图2所示。在物块M的下沉−振动中，对1号、3号子系统施加动载Fd(t)，使其发生强迫振动。
强迫振动由外部动载驱动，需要外部能量的持续输入。对于单自由度系统，其动力学控制方程可表示为
J¨z(t)+c˙z(t)+kz(t)=Fd(t)˙z(0)=˙z0, z(0)=z0 (2) 式(2)中的初始速度和初始位移可以同时为0。例如图2所示的振动，由动载Fd(t)触发，且由动载Fd(t)驱动，动力学过程中有外部能量的持续输入，系统的弹性势能增大了Gh/12。并且，在此类振动中，由于系统的结构未发生改变，系统的力学响应主要随着动载的变化而变化。图2中，由于Fd(∞)=G/6，导致瞬变后稳态时系统的受载由G/3阶变为G/2；如果Fd(∞)=0，则不会发生阶变。
1.2 矿震的力学原理与主控因子
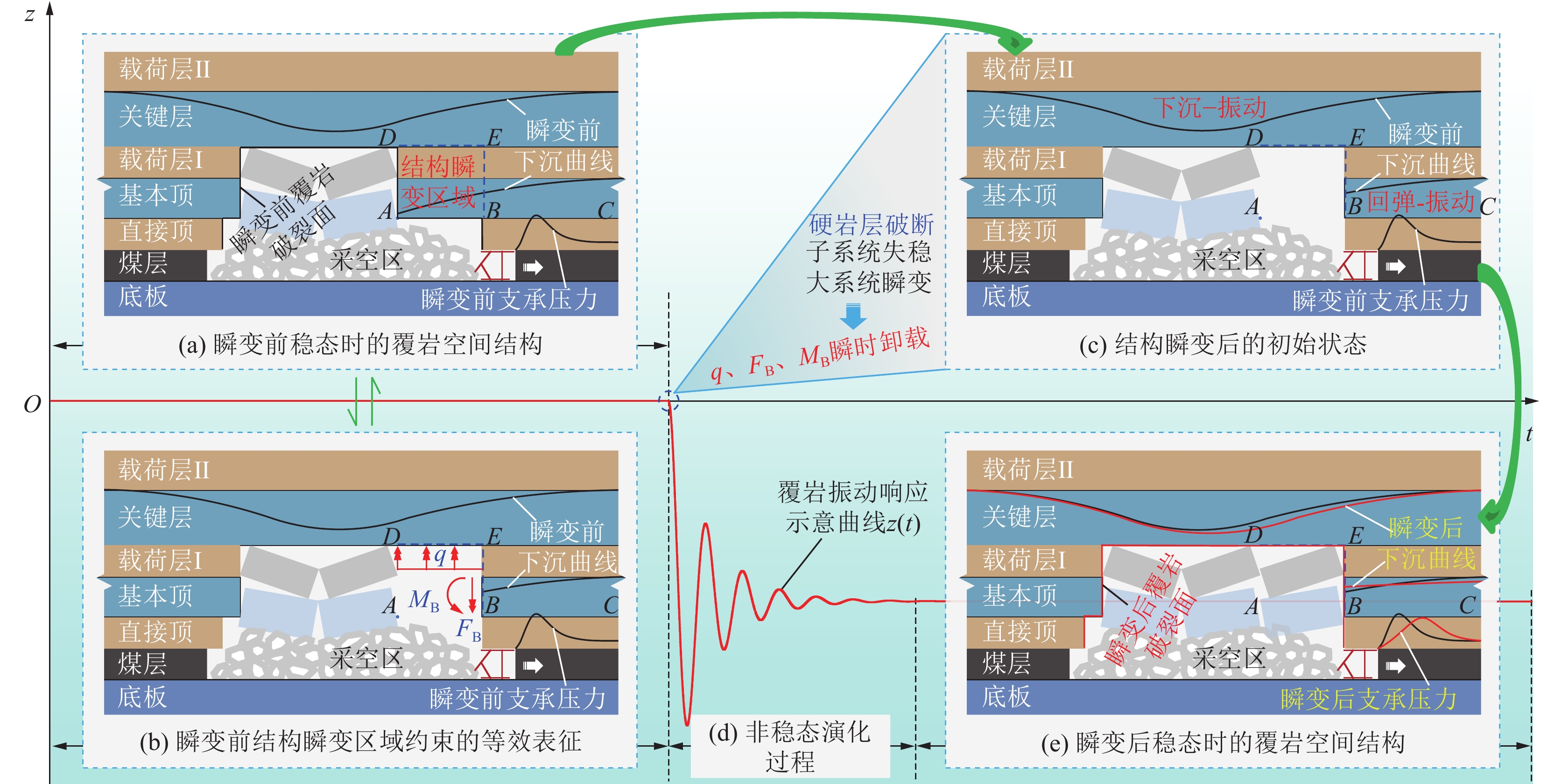
在地下煤层开采中，受自重应力场和采动卸荷效应影响，任意岩层都不是孤立存在的，覆岩破裂面以外、采动影响范围以内的岩层相互作用、相互制约，会自发形成一个类似于图1a所示、具有特殊力学联系的复杂煤岩力学系统，即覆岩空间结构[21-22]，如图3a所示。覆岩空间结构的力学功能是将采空区上方、覆岩破裂面外未破坏岩层的自重载荷转移至采空区四周的煤岩上，对覆岩载荷的大范围传递演化，及其作用下采场煤岩动静力学响应的研究具有重要意义。
![图 3 结构瞬变激励下采场煤岩动态力学响应发生与静态力学响应阶变机理示意]()
图 3 结构瞬变激励下采场煤岩动态力学响应发生与静态力学响应阶变机理示意Figure 3. Schematic diagram of the occurrence of dynamic mechanical response and the step change of static mechanical response of coal and rock in the mining area under structural transient excitation1.2.1 矿震的力学原理
回采过程中，当图3a中基本顶AC的悬露长度达到其临界破断步距时，基本顶破断。由于坚硬岩层具有瞬时破断的力学特性，基本顶AC的破断，意味着覆岩空间结构内边界的几何形态与约束发生了瞬变，等效于图3b中结构瞬变区域的约束载荷q、FB、MB被瞬时卸载(激励载荷)。对照1.1小节的振动分析可知，在力学原理上，图3中基本顶AC的瞬时破断及其形成的卸荷效应，与图1中2号子系统的瞬时破坏及其形成的卸荷效应是一致的。因此，在图3c所示煤岩结构瞬变后的初始状态驱动下，覆岩空间结构将发生类似于图1所示的有阻尼自由振动，覆岩载荷传递路径发生改变，其影响范围内采场煤岩的受载特征由静态演变为动载，将发生类似于图2所示的有阻尼强迫振动，直至图3e所示结构瞬变后的稳态，采场煤岩的静态力学响应发生阶变。
可以看出，在结构动力学视角下，坚硬岩层破断等采场煤岩结构子系统瞬时失稳触发的矿震，从整个采场煤岩结构的视角看，是一类典型的自由振动；对局部的煤岩而言，是典型的强迫振动。并且，由于采场煤岩结构远较图1所示的情况复杂，动力学过程中存在煤岩的损伤、破裂等情况，因此实际工程中的矿震应当是一类复杂的非线性、有阻尼自由振动。矿震中采场空间不同区域煤岩的力学响应存在显著差异，并非单纯的瞬时加卸载问题。例如，仅由载荷q、FB和MB变化情况可知，载荷q的瞬时卸载，会使关键层及其上覆岩层发生下沉−振动，释放重力势能，对其下方的载荷层Ⅰ瞬时加载。载荷FB、MB的瞬时卸载，会使岩层中的基本顶BC段发生向上的回弹−振动，释放应变能，对其上方的载荷层Ⅰ瞬时加载，并对其下方的煤体瞬时卸载。
需注意的是，载荷q、FB和MB的瞬时卸载，还会使覆岩载荷的传递路径发生改变，导致采场空间不同区域煤岩的受载特征与力学响应会随之改变。例如，对于基本顶而言，覆岩载荷传递路径的改变，会使其上表面被瞬时加载，导致基本顶BC段在回弹的同时，深部岩层中的部分区域会发生下沉，造成煤体支承压力的峰值减小、峰值位置向煤体深部跃迁[21]。事实上，上述煤体支承压力的阶变现象与切顶卸压后的情况一致[26-27]，都是采场煤岩结构改变后形成的结果。
可以看出，上述关于矿震的归类分析，有助于从根本上理解矿震的触发机理与演化机制，且其与现有矿震的定义在力学原理上是自洽的。例如，在本文的理念下，顶板运动型和断层错动型矿震，可以视作是基于本文采场煤岩结构失稳子系统的基本特征定义的；而张拉、张剪、纯剪、压剪等类型矿震，可以视作是基于本文采场煤岩结构失稳子系统的破坏类型定义的。
1.2.2 矿震的主控因子
由于力学响应受控于力学系统自身的力学性能与力学环境，以及输入激励载荷的基本特征。由此不难推断，矿震中采场煤岩的力学响应也受控于采场煤岩结构的力学性能与力学环境，及其对应的瞬变特征(卸荷效应)。
在激励载荷方面，输入激励载荷的大小、方向和作用位置都会对矿震中采场煤岩的力学响应产生不同程度的影响。仅就大小而言，图3中基本顶的厚度、强度、破断步距等越大，对应结构瞬变区域的q、FB、MB就越大，当其破断后采场煤岩结构力学性能与力学环境的瞬变特征越明显，形成的瞬时卸荷效应(激励载荷)越显著，诱发的动静力学响应特征会越明显。
在力学系统方面，即使在相同激励载荷作用下，由于不同矿区的煤岩赋存环境、开采设计等存在差异，导致其对应的采场煤岩结构存在差异，造成其对应的动静力学响应特征也必然会存在差异。此外，由上述理念不难得出，当临近地表的坚硬岩层破断后，会对其下方的煤岩形成瞬时卸载，采场煤岩会发生向上的回弹−振动，此种情况的矿震对地表的影响远大于地下。
同时，由上述矿震主控因子的分析可知，在实际工程中，可基于“调结构、控响应”的理念，建立针对性的防控措施。这其中，“调结构”包含对采场煤岩结构及其瞬变特征2个方面的调控。例如，在现有的防控措施中，对坚硬岩层水力压裂等，可以改变坚硬岩层的破断步距，相当于减小了结构瞬变程度与激励载荷，可实现在振源处消震的目的；而上保护层开采，会改变采场煤岩结构，不仅改变了受控对象(如煤层)的应力状态，亦相当于在振源与受控对象之间添加了一个隔振器，改变了采场煤岩结构的传递函数和能量释放速率等，可实现降载、隔振的目的。
由此可见，矿震是一类典型的自由振动，由坚硬岩层破断等采场煤岩结构子系统的瞬时失稳触发，由采场煤岩结构瞬变后的初始状态驱动，不需要外部能量的输入，耗散采场煤岩自身的势能(重力势能+应变能)。并且，矿震中采场煤岩的力学响应特征受控于采场煤岩结构的力学性能与力学环境，及其对应的瞬变特征。以下基于结构动力学理论，进一步分析采场煤岩的动静力学响应特征。
2. 覆岩的下沉−振动响应特征力学分析
伍永平等[22]已初步分析了基本顶破断后其岩层中部分向上的回弹−振动特征，为此，下文主要探讨结构瞬变区域上方覆岩的下沉−振动响应特征。同时，由于基本顶初次破断后采场煤岩结构的瞬变特征及其诱发的力学响应具有对称性，理论分析简单且便于理解，下面以基本顶初次破断时的情况为例进行分析。
2.1 关键层的受载特征与力学模型
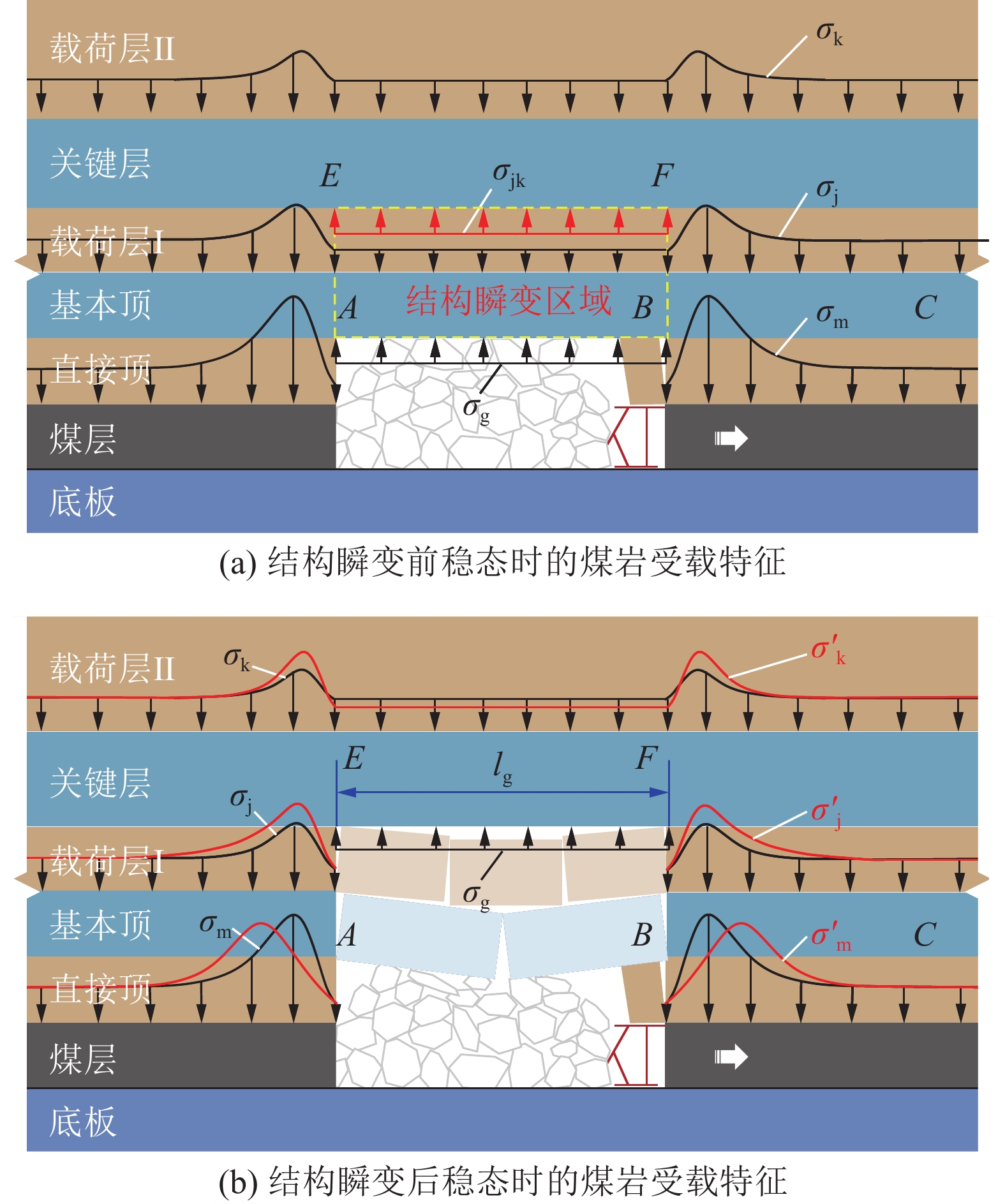
结合图3所示的力学分析，可构建图4所示结构瞬变激励下采场煤岩受载阶变发生机理的示意。图4中，σm、σj和σk分别为结构瞬变前稳态时作用在煤体、基本顶和关键层上的支承压力，MPa；σ´m、σ´j和σ´k分别为结构瞬变后稳态时作用在煤体、基本顶和关键层上的支承压力，MPa；σjk为结构瞬变前稳态时采空区上方载荷层Ⅰ对关键层的支撑载荷，MPa；σg为采空区矸石的支承压力，MPa；lg为基本顶的初次破断步距，m。以下分析中，以采空区中部为坐标原点O，以工作面推进方向为x轴，以铅垂方向为z轴。
![图 4 结构瞬变激励下煤岩受载阶变发生机理示意]()
图 4 结构瞬变激励下煤岩受载阶变发生机理示意Figure 4. Schematic diagram of step change mechanism of load on coal rock under structural transient excitation结合图3所示的力学分析，并通过对比图4所示基本顶初次破断前、后2个稳态时采场煤岩的受载特征可知，基本顶破断后，关键层的受载特征会发生瞬时的改变。具体表现为：
1)在基本顶的破断过程中，采空区上方EF段关键层下表面的受载量由σjk演变为σg。由于层间载荷σjk远大于矸石支撑载荷σg，即σjk > σg。因此，基本顶的破断，会在采空区上方EF段关键层的下表面形成瞬时卸载。
2)受基本顶破断的瞬时卸荷效应影响，关键层及其上覆岩层下沉，产生非均匀变形，覆岩载荷传递路径改变，在采空区上方的未破坏岩层中形成应力释放区，导致作用在EF段关键层上表面的载荷量会瞬时减小。
3)关键层未破断前，受采动影响，不同区域关键层上表面的受载特征存在差异，但其上表面的总承载量始终保持不变。因此，EF段关键层上表面承载量的瞬时减小，意味着采空区外侧关键层上表面的承载量会瞬时增大。
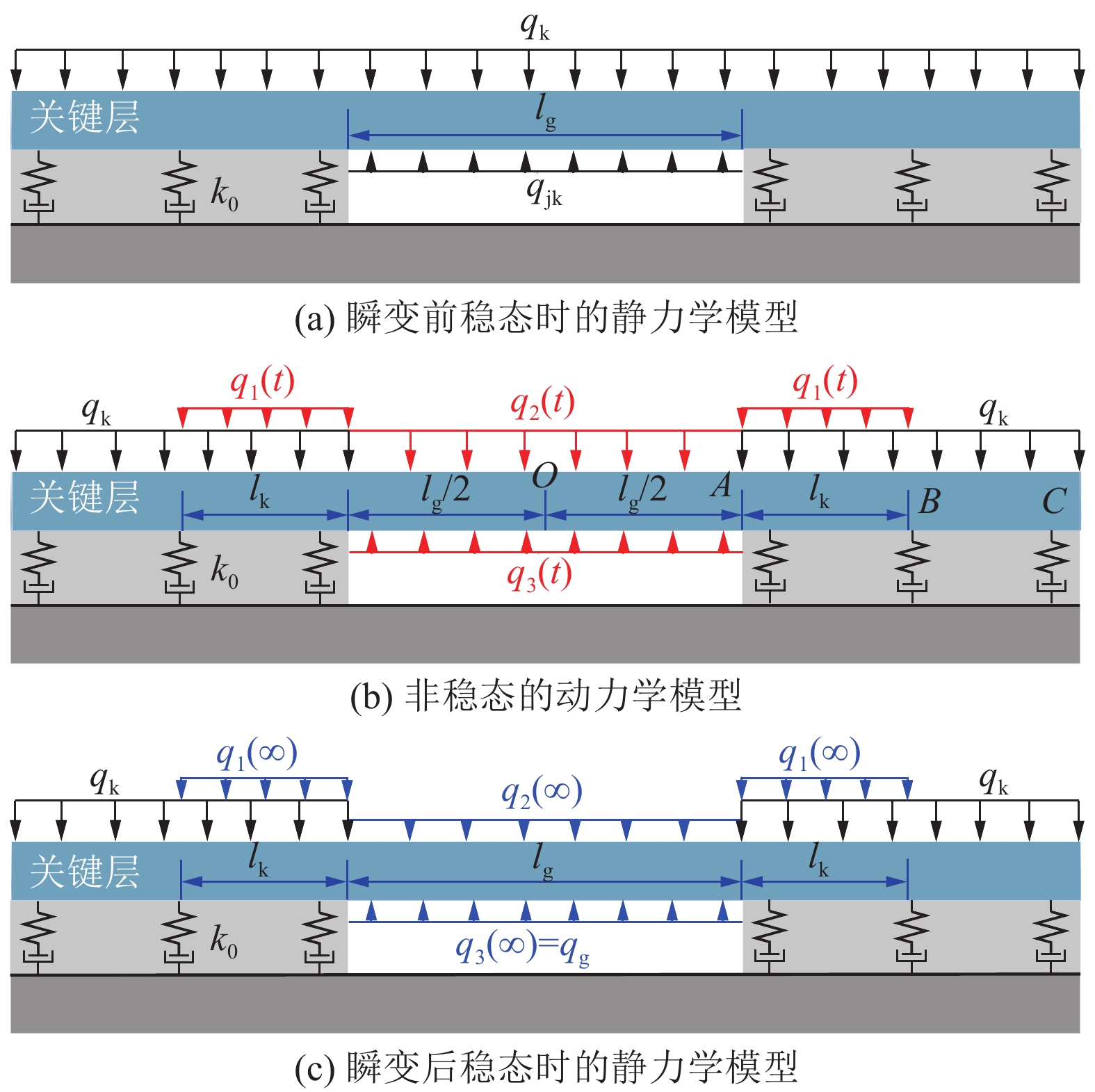
据此，沿倾向取单位宽度，并将作用载荷简化为均布载荷，可构建图5所示关键层岩梁的力学模型。图5中，qk为结构瞬变前稳态时作用在关键层上表面的载荷，kN/m；qjk为结构瞬变前稳态时采空区上方载荷层Ⅰ对关键层的支撑载荷，kN/m；qg为采空区矸石的支承压力，kN/m；q3(t)、q2(t)和q1(t)为对应上述3种情况的动载，kN/m；lk为关键层上转移载荷q1(t)的作用范围，m。
![图 5 结构瞬变激励下关键层岩梁的力学模型]()
图 5 结构瞬变激励下关键层岩梁的力学模型Figure 5. Mechanical model of key stratum rock beam under structural transient excitation结合采场煤岩的受载特征和运移规律，简化期间，这里假设图5b中的动载q1(t)、q2(t)和q3(t)均满足指数增大或衰减的模式，即：
q1(t)=q1(∞)(1−e−λ1t) (3) q2(t)=qk−[qk−q2(∞)](1−e−λ2t) (4) q3(t)=qjk−[qjk−q3(∞)](1−e−λ3t) (5) 式中：λ1、λ2和λ3为无量纲系数。结合图4，以及图5a和图5c所示结构瞬变前、后2个稳态时的情况可知，q1(0)=0、q2(0)=qk、q3(0)=qjk、q3(∞)=qg。同时，由铅垂方向的平衡条件，可得q1(∞)和q2(∞)需满足[22]：
2∫lg/lg22+lklg/lg22q1(∞)dx=∫lg/lg22−lg/−lg22[qk−q2(∞)]dx (6) 2.2 煤岩动力学响应力学分析
对于图5b所示关键层岩梁的动力学模型，由结构动力学理论[23]，可得其动力学控制方程为
EI∂4z(x,t)∂x4+ρA∂2z(x,t)∂t2+c∂z(x,t)∂t+k0z(x,t)=q(x,t) (7) 式中：z(x, t)为位移，m；ρ为密度，kg/m3；A为横截面面积，m2；E为弹性模量，kN/m2；I为惯性矩，m4；k0为地基系数，kN/m3。q(x, t)为作用在关键层岩梁上的载荷，可表示为
q(x,t)={q2(t)−q3(t)0⩽ (8) 对于图5b中关键层岩梁的OA段，将式(7)中的k0赋为0。对于式(7)所示的偏微分方程，由分离变量法[28]，可得图5b中关键层岩梁OA段的位移方程zOA(x, t)为
\begin{split} {{\textit{z}}_{{{OA}}}}(x,t) =& \bigg(\frac{{{q_2}(t) - {q_3}(t)}}{{24{{EI}}}}{x^4} + \frac{{{Q_0}}}{{6{{EI}}}}{x^3} + \frac{{{M_0}}}{{2{{EI}}}}{x^2} \\ &+ {A_0}x + {B_0}\bigg){{\mathrm{e}}^{ - \lambda t}}(\cos {\omega _{\mathrm{d}}}t + {E_0}\sin {\omega _{\mathrm{d}}}t) + \frac{{{Q_1}}}{{6{{EI}}}}{x^3} \\ &+ \frac{{{q_2}(\infty ) - {q_3}(\infty )}}{{24{{EI}}}}{x^4} + \frac{{{M_1}}}{{2{{EI}}}}{x^2} + {C_0}x + {D_0} \end{split} (9) 同理，AB段的位移方程zAB(x, t)为
\begin{split} {{\textit{z}}_{{{AB}}}}(x,t) =& [{{\mathrm{e}}^{ - {\beta _1}x}}({A_1}\cos {\beta _1}x + {B_1}\sin {\beta _1}x) \\ &+ {{\mathrm{e}}^{{\beta _1}x}}({C_1}\cos {\beta _1}x + {D_1}\sin {\beta _1}x)]{{\mathrm{e}}^{ - \lambda t}}(\cos {\omega _{\mathrm{d}}}t \\ &+ {E_1}\sin {\omega _{\mathrm{d}}}t) + {{\mathrm{e}}^{ - {\beta _1}x}}({A_2}\cos {\beta _0}x + {B_2}\sin {\beta _0}x) \\ &+ {{\mathrm{e}}^{{\beta _1}x}}({C_2}\cos {\beta _0}x + {D_2}\sin {\beta _0}x) + \frac{{{q_{\text{k}}} + {q_1}(t)}}{{{{{k}}_0}}} \end{split} (10) BC段的位移方程zBC(x, t)为
\begin{split} {{\textit{z}}_{{{BC}}}}(x,t) =& {{\mathrm{e}}^{ - {\beta _1}x}}({A_3}\cos {\beta _1}x \\ &+ {B_3}\sin {\beta _1}x){{\mathrm{e}}^{ - \lambda t}}(\cos {\omega _{\mathrm{d}}}t + {E_2}\sin {\omega _{\mathrm{d}}}t) \\ &+ {{\mathrm{e}}^{ - {\beta _0}x}}({C_3}\cos {\beta _0}x + {D_3}\sin {\beta _0}x) + \frac{{{q_{\text{k}}}}}{{{{{k}}_0}}} \end{split} (11) \mathit{\lambda } {=c/2\rho A} (12) {\omega } _{ \rm{d} } = {\omega } _{ \rm{n} } {(1-} {\lambda } ^{ {2}} {/\omega } _{ \rm{n} }^{{2}} {)}^{ {0.5}} (13) 式中：λ为衰减系数，s·m2；ωd为阻尼固有频率；ωn为弹性地基梁无阻尼时的固有频率；β0和β1分别为初始静平衡和动态演化过程中的弹性地基梁常量，m−1；Ai、Bi、Ci、Di和Ei为未知系数(i=0，1，2，3)；Q0、Q1为动态演化过程和结构瞬变后稳态时A截面的剪力，N；M0、M1为动态演化过程和结构瞬变后稳态时A截面的弯矩，N·m。可通过对应的边界条件、初始条件、连续性条件求解。由初始条件可得：
\frac{{\partial {{\textit{z}}_{{{OA}}}}(x,{\text{t}})}}{{\partial t}}\left| {_{t = 0}} \right. = \frac{{\partial {{\textit{z}}_{{{AB}}}}(x,{\text{t}})}}{{\partial t}}\left| {_{t = 0}} \right. = \frac{{\partial {{\textit{z}}_{{{BC}}}}(x,{\text{t}})}}{{\partial t}}\left| {_{t = 0}} \right. = 0 (14) 由O截面的初始条件和边界条件可得
\begin{split} &\left.\dfrac{\partial {\textit{z}}_{{OA}}(x, t)}{\partial x}\right|_{\substack{x=0 \\ t=0}}=0, \left.\dfrac{\partial^3 {\textit{z}}_{{OA}}(x, t)}{\partial x^3}\right|_{\substack{x=0 \\ t=0}}=0 \\ &\left.\dfrac{\partial {\textit{z}}_{{OA}}(x, t)}{\partial x}\right|_{\substack{x=0 \\ t=\infty}}=0, \left.\dfrac{\partial^3 {\textit{z}}_{{OA}}(x, t)}{\partial x^3}\right|_{\substack{x=0 \\ t=\infty}}=0 \end{split} (15) 由A截面的初始条件和连续性条件可得：
\begin{split} & {{\textit{z}}_{{{OA}}}}(x,t)\left| {_{\begin{subarray}{l} x = {l_{\mathrm{g}}}/2 \\ t = 0 \end{subarray} }} \right. = {{\textit{z}}_{{{AB}}}}(x,t)\left| {_{\begin{subarray}{l} x = {l_{\mathrm{g}}}/2 \\ t = 0 \end{subarray} }} \right. \\ & \frac{{\partial {{\textit{z}}_{{{OA}}}}(x,t)}}{{\partial x}}\left| {_{\begin{subarray}{l} x = {l_{\mathrm{g}}}/2 \\ t = 0 \end{subarray} }} \right. = \frac{{\partial {{\textit{z}}_{{{AB}}}}(x,t)}}{{\partial x}}\left| {_{\begin{subarray}{l} x = {l_{\mathrm{g}}}/2 \\ t = 0 \end{subarray} }} \right. \\ & \frac{{{\partial ^2}{{\textit{z}}_{{{OA}}}}(x,t)}}{{\partial {x^2}}}\left| {_{\begin{subarray}{l} x = {l_{\mathrm{g}}}/2 \\ t = 0 \end{subarray}} } \right. = \frac{{{\partial ^2}{{\textit{z}}_{{{AB}}}}(x,t)}}{{\partial {x^2}}}\left| {_{\begin{subarray}{l} x = {l_{\mathrm{g}}}/2 \\ t = 0 \end{subarray} }} \right. \\ & \frac{{{\partial ^3}{{\textit{z}}_{{{OA}}}}(x,t)}}{{\partial {x^3}}}\left| {_{\begin{subarray}{l} x = {l_{\mathrm{g}}}/2 \\ t = 0 \end{subarray}} } \right. = \frac{{{\partial ^3}{{\textit{z}}_{{{AB}}}}(x,t)}}{{\partial {x^3}}}\left| {_{\begin{subarray}{l} x = {l_{\mathrm{g}}}/2 \\ t = 0 \end{subarray}} } \right. \end{split} (16) \begin{split} & {{\textit{z}}_{{{OA}}}}(x,t)\left| {_{\begin{subarray}{l} x = {l_{\mathrm{g}}}/2 \\ t = \infty \end{subarray}} } \right. = {{\textit{z}}_{{{AB}}}}(x,t)\left| {_{\begin{subarray}{l} x = {l_{\mathrm{g}}}/2 \\ t = \infty \end{subarray}} } \right. \\ & \frac{{\partial {{\textit{z}}_{{{OA}}}}(x,t)}}{{\partial x}}\left| {_{\begin{subarray}{l} x = {l_{\mathrm{g}}}/2 \\ t = \infty \end{subarray} }} \right. = \frac{{\partial {{\textit{z}}_{{{AB}}}}(x,t)}}{{\partial x}}\left| {_{\begin{subarray}{l} x = {l_{\mathrm{g}}}/2 \\ t = \infty \end{subarray} }} \right. \\ & \frac{{{\partial ^2}{{\textit{z}}_{{{OA}}}}(x,t)}}{{\partial {x^2}}}\left| {_{\begin{subarray}{l} x = {l_{\mathrm{g}}}/2 \\ t = \infty \end{subarray}} } \right. = \frac{{{\partial ^2}{{\textit{z}}_{{{AB}}}}(x,t)}}{{\partial {x^2}}}\left| {_{\begin{subarray}{l} x = {l_{\mathrm{g}}}/2 \\ t = \infty \end{subarray}} } \right. \\ & \frac{{{\partial ^3}{{\textit{z}}_{{{OA}}}}(x,t)}}{{\partial {x^3}}}\left| {_{\begin{subarray}{l} x = {l_{\mathrm{g}}}/2 \\ t = \infty \end{subarray}} } \right. = \frac{{{\partial ^3}{{\textit{z}}_{{{AB}}}}(x,t)}}{{\partial {x^3}}}\left| {_{\begin{subarray}{l} x = {l_{\mathrm{g}}}/2 \\ t = \infty \end{subarray} }} \right. \end{split} (17) 由B截面的初始条件和连续性条件可得：
\begin{split} & {{\textit{z}}_{{{AB}}}}(x,t)\left| {_{\begin{subarray}{l} x = {l_{\mathrm{g}}}/2 + {l_{\mathrm{k}}} \\ t = 0 \end{subarray} }} \right. = {{\textit{z}}_{{{BC}}}}(x,t)\left| {_{\begin{subarray}{l} x = {l_{\mathrm{g}}}/2 + {l_{\mathrm{k}}} \\ t = 0 \end{subarray}} } \right. \\ & \frac{{\partial {{\textit{z}}_{{{AB}}}}(x,t)}}{{\partial x}}\left| {_{\begin{subarray}{l} x = {l_{\mathrm{g}}}/2 + {l_{\mathrm{k}}} \\ t = 0 \end{subarray} }} \right. = \frac{{\partial {{\textit{z}}_{{{BC}}}}(x,t)}}{{\partial x}}\left| {_{\begin{subarray}{l} x = {l_{\mathrm{g}}}/2 + {l_{\mathrm{k}}} \\ t = 0 \end{subarray}} } \right. \\ & \frac{{{\partial ^2}{{\textit{z}}_{{{AB}}}}(x,t)}}{{\partial {x^2}}}\left| {_{\begin{subarray}{l} x = {l_{\mathrm{g}}}/2 + {l_{\mathrm{k}}} \\ t = 0 \end{subarray} }} \right. = \frac{{{\partial ^2}{{\textit{z}}_{{{BC}}}}(x,t)}}{{\partial {x^2}}}\left| {_{\begin{subarray}{l} x = {l_{\mathrm{g}}}/2 + {l_{\mathrm{k}}} \\ t = 0 \end{subarray}} } \right. \\ & \frac{{{\partial ^3}{{\textit{z}}_{{{AB}}}}(x,t)}}{{\partial {x^3}}}\left| {_{\begin{subarray}{l} x = {l_{\mathrm{g}}}/2 + {l_{\mathrm{k}}} \\ t = 0 \end{subarray} }} \right. = \frac{{{\partial ^3}{{\textit{z}}_{{{BC}}}}(x,t)}}{{\partial {x^3}}}\left| {_{\begin{subarray}{l} x = {l_{\mathrm{g}}}/2 + {l_{\mathrm{k}}} \\ t = 0 \end{subarray} }} \right. \end{split} (18) \begin{split} & {{\textit{z}}_{{{AB}}}}(x,t)\left| {_{\begin{subarray}{l} x = {l_{\mathrm{g}}}/2 + {l_{\mathrm{k}}} \\ t = \infty \end{subarray}} } \right. = {{\textit{z}}_{{{BC}}}}(x,t)\left| {_{\begin{subarray}{l} x = {l_{\mathrm{g}}}/2 + {l_{\mathrm{k}}} \\ t = \infty \end{subarray}} } \right. \\ & \frac{{\partial {{\textit{z}}_{{{AB}}}}(x,t)}}{{\partial x}}\left| {_{\begin{subarray}{l} x = {l_{\mathrm{g}}}/2 + {l_{\mathrm{k}}} \\ t = \infty \end{subarray}} } \right. = \frac{{\partial {{\textit{z}}_{{{BC}}}}(x,t)}}{{\partial x}}\left| {_{\begin{subarray}{l} x = {l_{\mathrm{g}}}/2 + {l_{\mathrm{k}}} \\ t = \infty \end{subarray} }} \right. \\ & \frac{{{\partial ^2}{{\textit{z}}_{{{AB}}}}(x,t)}}{{\partial {x^2}}}\left| {_{\begin{subarray}{l} x = {l_{\mathrm{g}}}/2 + {l_{\mathrm{k}}} \\ t = \infty \end{subarray} }} \right. = \frac{{{\partial ^2}{{\textit{z}}_{{{BC}}}}(x,t)}}{{\partial {x^2}}}\left| {_{\begin{subarray}{l} x = {l_{\mathrm{g}}}/2 + {l_{\mathrm{k}}} \\ t = \infty \end{subarray}} } \right. \\ & \frac{{{\partial ^3}{{\textit{z}}_{{{AB}}}}(x,t)}}{{\partial {x^3}}}\left| {_{\begin{subarray}{l} x = {l_{\mathrm{g}}}/2 + {l_{\mathrm{k}}} \\ t = \infty \end{subarray} }} \right. = \frac{{{\partial ^3}{{\textit{z}}_{{{BC}}}}(x,t)}}{{\partial {x^3}}}\left| {_{\begin{subarray}{l} x = {l_{\mathrm{g}}}/2 + {l_{\mathrm{k}}} \\ t = \infty \end{subarray} }} \right. \end{split} (19) 由式(9)—式(19)可得出关键层岩梁的位移方程z(x, t)，进一步可求解关键层岩梁的速度、加速度、转角、弯曲应变能等力学响应。这其中，关键层岩梁的速度方程v(x, t)可表示为
v(x,t) = \frac{{\partial {\textit{z}}(x,t)}}{{\partial t}} (20) 同时，由材料力学理论[29]，可得关键层岩梁的弯曲应变能密度{v_\varepsilon } (x, ξ, t)可近似表示为
{v_\varepsilon }\left( {x,\xi ,t} \right) = \frac{1}{2}\sigma \varepsilon = \frac{1}{2}\frac{{M\left( {x,t} \right)}}{{\text{I}}}\frac{{{\xi ^2}}}{{R\left( {x,t} \right)}} (21) 式中：ξ为距中性轴距离，m；σ为弯曲正应力，Pa；ε为弯曲正应变；M(x, t)为弯矩方程，kN·m；R(x, t)为曲率半径，m。R(x, t)可表示为
R\left( {x,t} \right) = \frac{{{{\left\{ {1 + {{\left[ {\dfrac{{\partial {\textit{z}}\left( {x,t} \right)}}{{\partial x}}} \right]}^2}} \right\}}^{\tfrac{3}{2}}}}}{{\left| {\dfrac{{{\partial ^2}{\textit{z}}\left( {x,t} \right)}}{{\partial {x^2}}}} \right|}} (22) 将式(22)代入式(21)，并沿截面积分，可得任意x位置处弯曲应变能的线密度Eε(x, t)为
{E_\varepsilon }\left( {x,t} \right) = \frac{{E{h_0}^3}}{{24}}\frac{{{{\left[ {\dfrac{{{\partial ^2}{\textit{z}}\left( {x,t} \right)}}{{\partial {x^2}}}} \right]}^2}}}{{{{\left\{ {1 + {{\left[ {\dfrac{{\partial {\textit{z}}\left( {x,t} \right)}}{{\partial x}}} \right]}^2}} \right\}}^3}}} (23) 式中：h0为关键层岩梁的厚度，m。对式(23)沿x轴积分，可得到整个关键层岩梁的弯曲应变能随时间t的变化关系。
3. 算例分析
由于作用在关键层上的载荷均为上覆岩层的自重载荷，因此关键层垂直位移的演化规律可在某种程度上反映覆岩重力势能的演化规律。同时，由动能的定义可知，关键层速度的演化规律可反映其动能的演化规律。为此，以下主要探讨结构瞬变激励下关键层速度、位移和弯曲应变能线密度的动态响应特征，并在此基础上分析覆岩能量的转换、聚集与释放规律。
3.1 结构瞬变激励下关键层的下沉−振动响应特征
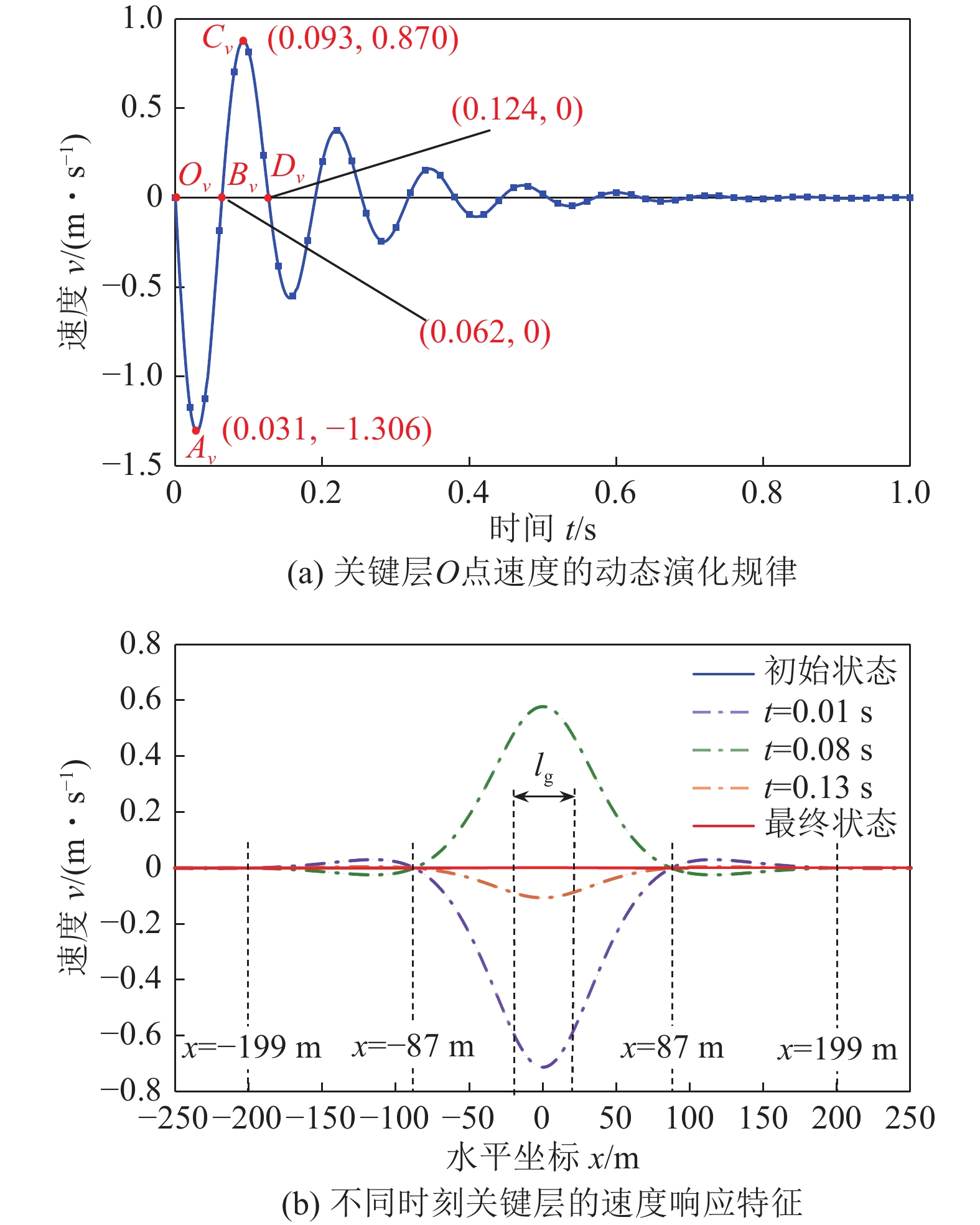
图6所示为关键层岩梁O点(x=0 m)位置处速度v(0, t)随时间的演化规律，以及不同时刻速度v(x, t)的响应特征。由图6中可以看出：
1)基本顶瞬时破断−卸荷后，关键层岩梁发生下沉−振动，由于基本顶初次破断后采场煤岩结构的瞬变特征具有对称性，导致其诱发的力学响应亦具有对称性。关键层岩梁O点(x=0 m)的速度最大，瞬时最大下沉速度为－1.306 m/s，瞬时最大回弹速度为0.870 m/s，二者绝对值的差值为0.436 m/s，如图6a所示。
2)在任意t时刻，关键层岩梁的速度响应都呈现出波动状态，且以振幅最大点(O点)为中心迅速衰减。例如，在t=0.08 s时，采空区中心右侧0 < x < 87 m范围内岩梁的速度向上，最大速度为0.577 m/s；87 m < x < 199 m范围内岩梁的速度向下，最大速度为－0.024 m/s；199 m < x < 255 m范围内岩梁的速度向上，最大速度为0.001 m/s，如图6b所示。
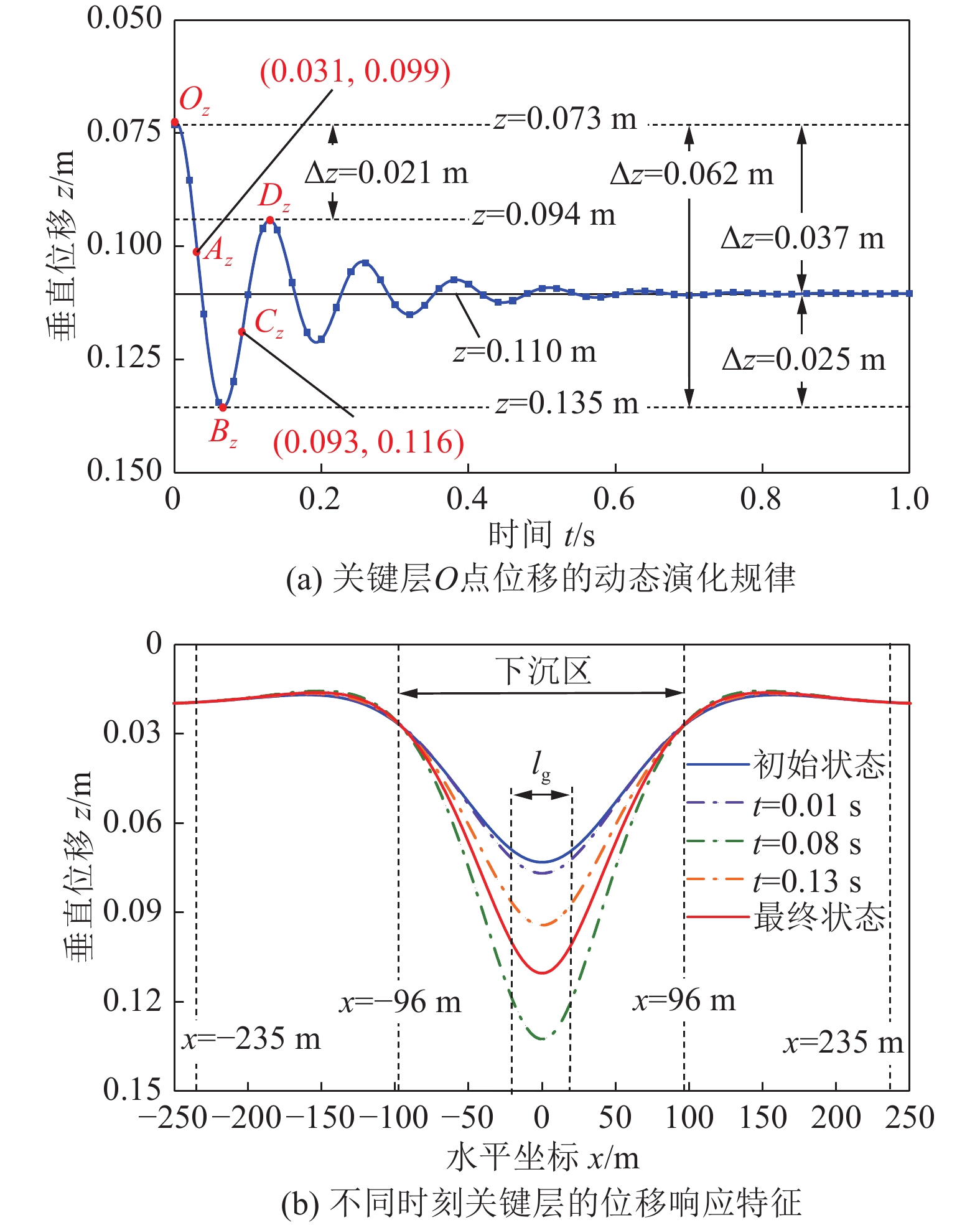
图7所示为关键层岩梁O点位置处位移z(0, t)随时间的演化规律，以及不同时刻位移z(x, t)的响应特征。由图7中可以看出：
![图 7 关键层岩梁的位移响应特征]()
图 7 关键层岩梁的位移响应特征Figure 7. Displacement response characteristics of key stratum rock beam1)基本顶瞬时破断后，关键层岩梁的瞬态响应是向下运动，且在其后续的振动过程中都不能回复到其初始位置。因此，在矿震中，覆岩重力会做功，重力势能会瞬时释放。例如，O点的最大下沉位移为0.135 m，相对于初值(0.073 m)的阶变量为0.062 m；最大回弹位移为0.094 m，相对于初值的阶变量为0.021 m；瞬变后稳态时的值为0.110 m，相对于初值的阶变量为0.037 m，如图7a所示。
2)受速度的波动响应特征影响，关键层岩梁位移的响应特征也具有波动特性，且以O点为中心迅速衰减。例如，在t=0.08 s时，相对于初始时刻而言，采空区中心右侧0 < x < 96 m范围内岩梁的位移阶变量为正值(下沉)，最大位移阶变量为0.059 3 m；96 m < x < 235 m范围内岩梁的位移阶变量为负值(翘曲)，最大位移阶变量为−0.002 m；235 m < x < 250 m范围内岩梁的位移阶变量为正值，最大位移阶变量为0.000 3 m，如图7b所示。同时可以看出，关键层岩梁的动态响应特征及其稳态时的阶变规律与已有的理论研究和现场实测结果在定性上是一致的，这也在某种程度上验证了本文理论模型的正确性[10, 21, 25]。
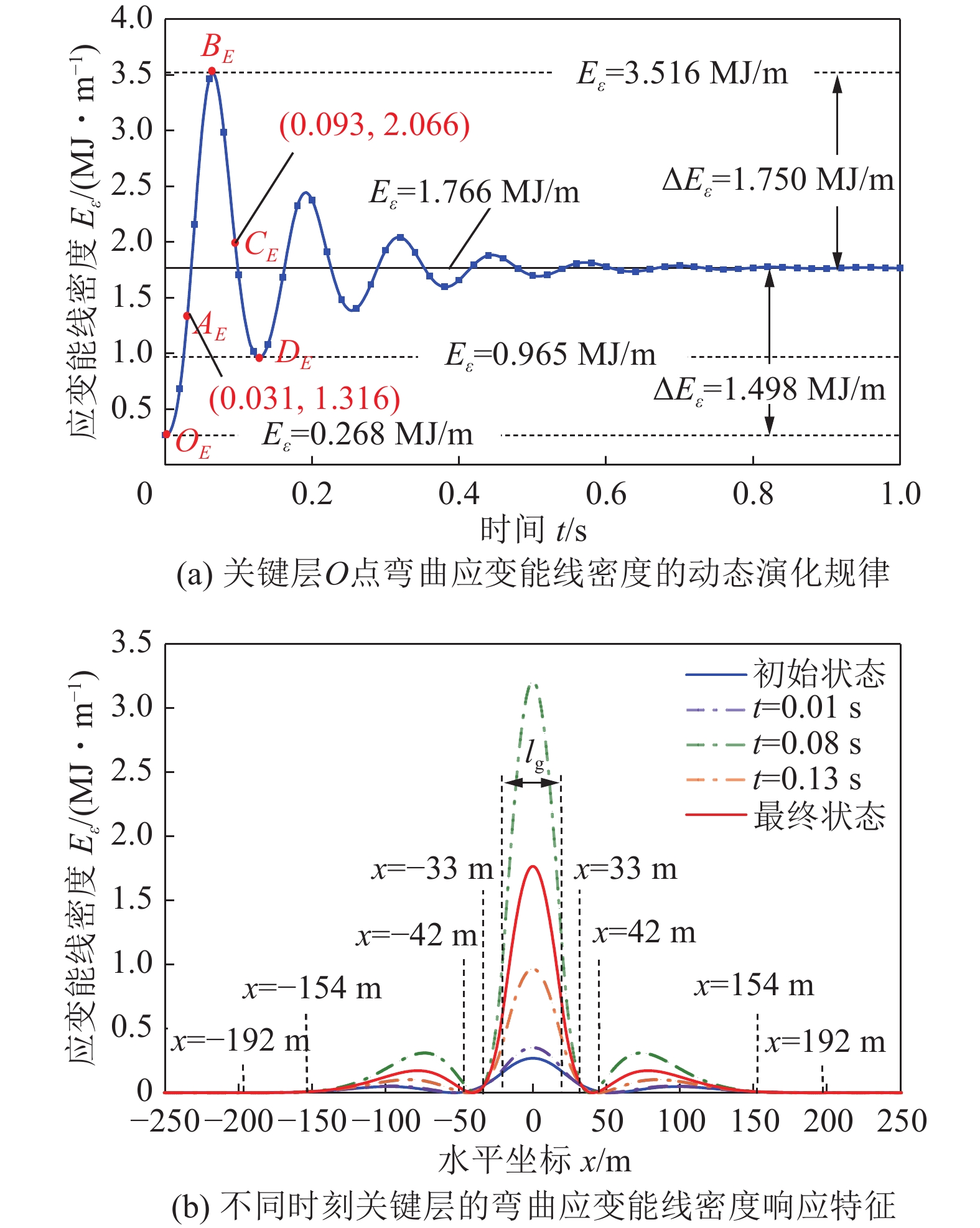
图8所示为关键层岩梁O点位置处弯曲应变能线密度Eε(0, t)随时间的演化规律，以及不同时刻弯曲应变能线密度Eε(x, t)的响应特征。由图8中可以看出：
![图 8 关键层岩梁的弯曲应变能线密度响应特征]()
图 8 关键层岩梁的弯曲应变能线密度响应特征Figure 8. Response characteristics of bending strain energy linear density of key stratum rock beam1)基本顶瞬时破断后，关键层岩梁的弯曲应变能线密度往复震荡，且在振动过程中始终大于其初值。因此，在矿震中，关键层的弯曲应变能增大。例如，O点弯曲应变能线密度的极值为3.516 MJ/m，相对于初值(0.268 MJ/m)的阶变量为3.248 MJ/m；瞬变后稳态时的值为1.766 MJ/m，相对于初值的阶变量为1.498 MJ/m，如图8a所示。
2)受位移(变形)的波动响应特征影响，关键层岩梁弯曲应变能线密度的响应特征也具有波动特性，且仍以O点为中心迅速衰减。例如，在t=0.08 s时，相对于初始时刻而言，采空区中心右侧0 < x < 33 m范围内岩梁应变能的阶变量为正值，最大阶变量为2.941 MJ/m；33 m < x < 42 m范围内的阶变量为负值，最大阶变量为－33.071 kJ/m；42 m < x < 154 m范围内的阶变量为正值，最大阶变量为287.180 kJ/m；154 m < x < 192 m范围内的阶变量为负值，最大阶变量为－962 J/m；192 m < x < 250 m范围内的阶变量为正值，最大阶变量为248 J/m，如图8b所示。
3.2 结构瞬变激励下覆岩能量的演变规律
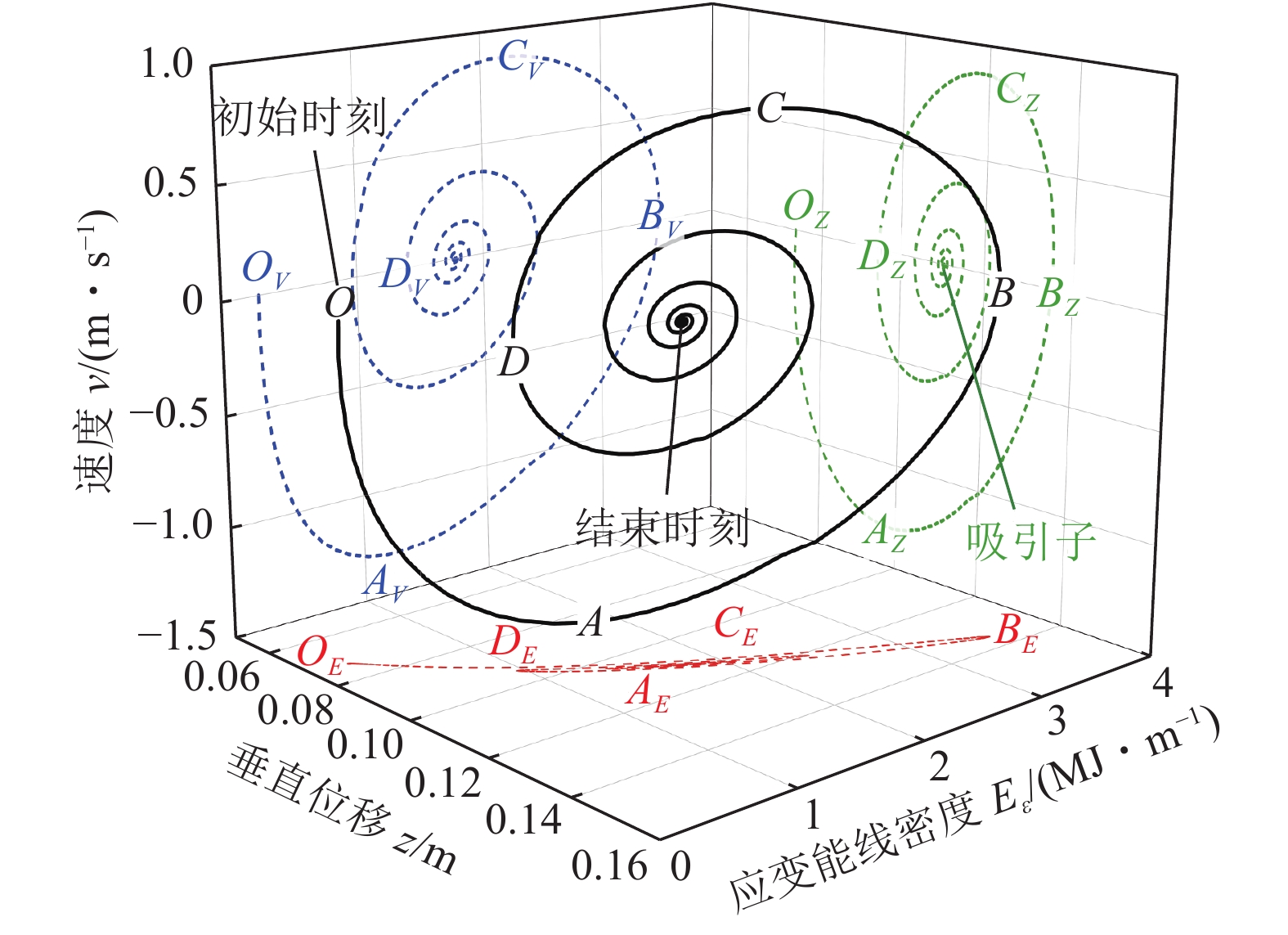
图9所示为关键层岩梁O点位移、速度和应变能线密度随时间演化的内在联系。由于O点的位移与重力势能(负相关)、速度与动能(正相关)、弯曲应变能线密度与应变能(正相关)之间存在对应关系，因此图9也反映了O点重力势能、应变能和动能的演变规律。为此，以下从能量的角度，分析第一个振动周期(0～0.126 s)内各能量的转换、聚集与释放规律(后续周期内的演化规律与之类似)。这其中，图6a中的点Ov、Av、Bv、Cv和Dv是对应图9中O、A、B、C、D时刻的速度点，图7a和图8a中的情况类似。由图9，并结合图6a、图7a和图8a可以看出：
![图 9 O点速度、位移和应变能线密度演化的内在联系]()
图 9 O点速度、位移和应变能线密度演化的内在联系Figure 9. Internal relations of velocity, displacement and strain energy linear density of point O during evolution1)在OA段，即0 < t < 0.031 s的第1个1/4周期内，关键层岩梁O点的重力势能持续释放，除了部分耗散外，其余转换为动能和应变能。该时间段内岩梁O点的速度由0 m/s持续增大至−1.306 m/s，垂直位移由0.075 m持续增大至0.099 m，应变能线密度由0.268 MJ/m持续增大至1.316 MJ/m。因此，该时间段内岩梁O点的重力势能持续减小，动能和应变能持续增大，即重力势能→动能+应变能。
2)在AB段，即0.031 s < t < 0.062 s的第2个1/4周期内，关键层岩梁O点的重力势能和动能持续释放，除了部分耗散外，其余转换为应变能。该时间段内岩梁O点的速度由−1.306 m/s持续减小至0 m/s，垂直位移由0.099 m持续增大至0.135 m，应变能线密度由1.316 MJ/m持续增大至3.516 MJ/m。因此，该时间段内岩梁O点的重力势能和动能持续减小，应变能持续增大，即重力势能+动能→应变能。
3)在BC段，即0.062 s < t < 0.093 s的第3个1/4周期内，关键层岩梁O点的应变能持续释放，除了部分耗散外，其余转换为重力势能和动能。该时间段内岩梁O点的速度由0 m/s持续增大至0.87 m/s，垂直位移由0.135 m持续减小至0.116 m，应变能线密度由3.516 MJ/m持续减小至2.066 MJ/m。因此，该时间段内岩梁O点的重力势能和动能持续增大，应变能持续减小，即应变能→重力势能+动能。
4)在CD段，即0.093 s < t < 0.124 s的第4个1/4周期内，关键层岩梁O点的动能和应变能持续释放，除了部分耗散外，其余转换为重力势能。该时间段内岩梁O点的速度由0.87 m/s持续减小至0 m/s，垂直位移由0.116 m持续减小至0.094 m，应变能线密度由2.066 MJ/m持续减小至0.965 MJ/m。因此，该时间段内岩梁O点的重力势能持续增大，动能和应变能持续减小，即动能+应变能→重力势能。
综合上述分析可以看出，矿震是一类典型的动力学问题，从整个采场煤岩结构的视角看，是典型的自由振动；对局部的煤岩而言，是典型的强迫振动；并且，矿震的主控因子是采场煤岩结构的力学性能与力学环境，及其对应的瞬变特征。在实际工程中，可结合具体工程背景，基于“调结构、控响应”的理念，建立针对性的防控措施。需说明的是，本文主要是通过近水平煤层开采坚硬岩层瞬时破断的情况，阐述了本文的理念，该理念亦可应用于断层、急倾斜煤层等特殊地质构造的情况。
4. 结 论
1)矿震是一类典型的有阻尼自由振动，由坚硬岩层破断等采场煤岩结构子系统的瞬时失稳触发，由采场煤岩结构瞬变后的初始状态驱动，不需要外部能量的输入，耗散采场煤岩自身的势能(重力势能+应变能)。并且，矿震中采场煤岩的力学响应受控于采场煤岩结构的力学性能与力学环境，及其对应的瞬变特征。
2)受基本顶的瞬时破断影响，采场煤岩结构发生瞬变，覆岩载荷传递路径随之改变，采空区上方覆岩应力释放，作用在采空区上方关键层上、下表面的载荷瞬时减小，作用在采空区外侧围岩中关键层上表面的载荷瞬时增大，关键层及其上覆岩层下沉−振动，重力做功、释放重力势能，并对其下方岩层形成瞬时的加载。
3)结构瞬变后，关键层及其上覆岩层的瞬态响应是向下运动，且在其后续的振动过程中都不能回复到其初始位置。因此，整体而言，覆岩的重力势能会减小，而应变能会增大。同时，在任意时刻，关键层岩梁速度、位移和弯曲应变能线密度等响应特征都呈现出波动状态，且都以震源为中心迅速衰减。
4)在任意振动周期内，除了有能量的耗散外，亦存在覆岩重力势能、应变能和动能的相互转换。这其中，在第1个1/4周期内，重力势能向动能和应变能转换；在第2个1/4周期内，重力势能和动能向应变能转换；在第3个1/4周期内，应变能向重力势能和动能转换；在第4个1/4周期内，动能和应变能向重力势能转换。
5)从结构动力学的理念和整个采场煤岩结构的视角分析，可以更直观地理解矿震的触发机理与主控因子，以及矿震中采场空间不同区域煤岩力学响应的发生机理及其内在关联。在实际工程中，可结合具体工程背景，基于煤岩结构与其力学响应的内在关联，采用“调结构、控响应”的理念，建立针对性的防控措施。
-
![]()
图 3 结构瞬变激励下采场煤岩动态力学响应发生与静态力学响应阶变机理示意
Figure 3. Schematic diagram of the occurrence of dynamic mechanical response and the step change of static mechanical response of coal and rock in the mining area under structural transient excitation
![]()
图 4 结构瞬变激励下煤岩受载阶变发生机理示意
Figure 4. Schematic diagram of step change mechanism of load on coal rock under structural transient excitation
![]()
图 5 结构瞬变激励下关键层岩梁的力学模型
Figure 5. Mechanical model of key stratum rock beam under structural transient excitation
![]()
图 7 关键层岩梁的位移响应特征
Figure 7. Displacement response characteristics of key stratum rock beam
![]()
图 8 关键层岩梁的弯曲应变能线密度响应特征
Figure 8. Response characteristics of bending strain energy linear density of key stratum rock beam
-
[1] Gibowicz S J,Kijko A. 矿山地震学引论[M]. 北京:地震出版社,1998. [2] 袁亮. 煤矿典型动力灾害风险判识及监控预警技术研究进展[J]. 煤炭学报,2020,45(5):1557−1566. YUAN Liang. Research progress on risk identification, assessment, monitoring and early warning technologies of typical dynamic hazards in coal mines[J]. Journal of China Coal Society,2020,45(5):1557−1566.
[3] 齐庆新,潘一山,舒龙勇,等. 煤矿深部开采煤岩动力灾害多尺度分源防控理论与技术架构[J]. 煤炭学报,2018,43(7):1801−1810. QI Qingxin, PAN Yishan, SHU Longyong, et al. Theory and technical framework of prevention and control with different sources in multi-scales for coal and rock dynamic disasters in deep mining of coal mines[J]. Journal of China Coal Society,2018,43(7):1801−1810.
[4] 曹安业,窦林名,白贤栖,等. 我国煤矿矿震发生机理及治理现状与难题[J]. 煤炭学报,2023,48(5):1894−1918. CAO Anye, DOU Linming, BAI Xianxi, et al. State-of-the-art occurrence mechanism and hazard control of mining tremors and their challenges in Chinese coal mines[J]. Journal of China Coal Society,2023,48(5):1894−1918.
[5] 窦林名,曹晋荣,曹安业,等. 煤矿覆岩矿震关键层及其破断释能机制[J]. 煤炭学报,2025,50(1):180−192. DOU Linming, CAO Jinrong, CAO Anye, et al. Key strata of mining-induced seismicity in overburden rocks in coal mines and the energy-releasing mechanism of its fracture[J]. Journal of China Coal Society,2025,50(1):180−192.
[6] 朱斯陶,刘金海,姜福兴,等. 我国煤矿整体失稳型冲击地压类型、发生机理及防治[J]. 煤炭学报,2020,45(11):3667−3677. ZHU Sitao, LIU Jinhai, JIANG Fuxing, et al. Types, occurcenec mechanism and prevention of overall istability induced rockbursts in China coal mines[J]. Journal of China Coal Society,2020,45(11):3667−3677.
[7] 潘一山,宋义敏,刘军. 我国煤矿冲击地压防治的格局、变局和新局[J]. 岩石力学与工程学报,2023,42(9):2081−2095. PAN Yishan, SONG Yimin, LIU Jun. Pattern, change and new situation of coal mine rockburst prevention and control in China[J]. Chinese Journal of Rock Mechanics and Engineering,2023,42(9):2081−2095.
[8] 蔡武,窦林名,王桂峰,等. 煤层采掘活动引起断层活化的力学机制及其诱冲机理[J]. 采矿与安全工程学报,2019,36(6):1193−1202. CAI Wu, DOU Linming, WANG Guifeng, et al. Mechanism of fault reactivation and its induced coal burst caused by coal mining activities[J]. Journal of Mining & Safety Engineering,2019,36(6):1193−1202.
[9] 朱建波,马斌文,谢和平,等. 煤矿矿震与冲击地压的区别与联系及矿震扰动诱冲初探[J]. 煤炭学报,2022,47(9):3396−3409. ZHU Jianbo, MA Binwen, XIE Heping, et al. Differences and connections between mining seismicity and coal bursts in coal mines and preliminary study on coal bursts induced by mining seismicity[J]. Journal of China Coal Society,2022,47(9):3396−3409.
[10] 杜涛涛. 矿震震动传播与响应规律[J]. 岩土工程学报,2018,40(3):418−425. DU Taotao. Propagation and response laws of mine seism[J]. Chinese Journal of Geotechnical Engineering,2018,40(3):418−425.
[11] 王恩元,冯俊军,张奇明,等. 冲击地压应力波作用机理[J]. 煤炭学报,2020,45(1):100−110. WANG Enyuan, FENG Junjun, ZHANG Qiming, et al. Mechanism of rockburst under stress wave in mining space[J]. Journal of China Coal Society,2020,45(1):100−110.
[12] 高明仕,徐东,贺永亮,等. 厚硬顶板覆岩冲击矿震影响的远近场效应研究[J]. 采矿与安全工程学报,2022,39(2):215−226. GAO Mingshi, XU Dong, HE Yongliang, et al. Investigation on the near-far field effect of rock burst subject to the breakage of thick and hard overburden[J]. Journal of Mining & Safety Engineering,2022,39(2):215−226.
[13] 潘俊锋,夏永学,王书文,等. 我国深部冲击地压防控工程技术难题及发展方向[J]. 煤炭学报,2024,49(3):1291−1302. PAN Junfeng, XIA Yongxue, WANG Shuwen, et al. Technical difficulties and emerging development directions of deep rock burst prevention in China[J]. Journal of China Coal Society,2024,49(3):1291−1302.
[14] 朱斯陶,刘金海,姜福兴,等. 我国煤矿顶板运动型矿震及诱发灾害分类、预测与防控[J]. 煤炭学报,2022,47(2):807−816. ZHU Sitao, LIU Jinhai, JIANG Fuxing, et al. Classification, prediction, prevention and control of roof movement-type mine earthquakes and induced disasters in China’s coal mines[J]. Journal of China Coal Society,2022,47(2):807−816.
[15] CAI W, BAI X X, SI G Y, et al. A monitoring investigation into rock burst mechanism based on the coupled theory of static and dynamic stresses[J]. Rock Mechanics and Rock Engineering,2020,53(12):5451−5471. doi: 10.1007/s00603-020-02237-6
[16] 陈结,杜俊生,蒲源源,等. 冲击地压“双驱动” 智能预警架构与工程应用[J]. 煤炭学报,2022,47(2):791−806. CHEN Jie, DU Junsheng, PU Yuanyuan, et al. “Dual-driven” intelligent pre-warning framework of the coal burst disaster in coal mine and its engineering application[J]. Journal of China Coal Society,2022,47(2):791−806.
[17] 谭云亮,张修峰,肖自义,等. 冲击地压主控因素及孕灾机制[J]. 煤炭学报,2024,49(1):367−379. TAN Yunliang, ZHANG Xiufeng, XIAO Ziyi, et al. Main control factors of rock burst and its disaster evolution mechanism[J]. Journal of China Coal Society,2024,49(1):367−379.
[18] 康红普,姜鹏飞,黄炳香,等. 煤矿千米深井巷道围岩支护−改性−卸压协同控制技术[J]. 煤炭学报,2020,45(3):845−864. KANG Hongpu, JIANG Pengfei, HUANG Bingxiang, et al. Roadway strata control technology by means of bolting-modification-destressing in synergy in 1 000 m deep coal mines[J]. Journal of China Coal Society,2020,45(3):845−864.
[19] 潘一山,齐庆新,王爱文,等. 煤矿冲击地压巷道三级支护理论与技术[J]. 煤炭学报,2020,45(5):1585−1594. PAN Yishan, QI Qingxin, WANG Aiwen, et al. Theory and technology of three levels support in bump-prone roadway[J]. Journal of China Coal Society,2020,45(5):1585−1594.
[20] 姜福兴,张翔,朱斯陶. 煤矿冲击地压防治体系中的关键问题探讨[J]. 煤炭科学技术,2023,51(1):203−213. JIANG Fuxing, ZHANG Xiang, ZHU Sitao. Discussion on key problems in prevention and control system of coal mine rock burst[J]. Coal Science and Technology,2023,51(1):203−213.
[21] 罗生虎,王同,伍永平,等. 结构瞬变激励下采场煤岩的力学响应[J]. 煤炭学报,2023,48(12):4406−4416. LUO Shenghu, WANG Tong, WU Yongping, et al. Mechanical response of coal and rock in stope under transient excitation of structure[J]. Journal of China Coal Society,2023,48(12):4406−4416.
[22] 伍永平,罗生虎,闫壮壮,等. 煤岩结构瞬变诱冲机理[J]. 煤炭学报,2025,50(1):193−208. WU Yongping, LUO Shenghu, YAN Zhuangzhuang, et al. The mechanism of rockburst induced by coal rock structure transient[J]. Journal of China Coal Society,2025,50(1):193−208.
[23] 于开平,邹经湘. 结构动力学[M]. 哈尔滨:哈尔滨工业大学出版社,2015. [24] 邱泽华,石耀霖. 地震造成远距离应力阶变的观测实例[J]. 中国科学(D辑:地球科学),2003,33(S1):60−64. QIU Zehua, SHI Yaolin. Observation example of long-distance stress step change caused by earthquake[J]. Scientia Sinica (Terrae),2003,33(S1):60−64.
[25] 唐岳松,孙文超,李增强,等. 冲击地压矿井充填开采工作面采动应力激增与跌落机制[J]. 煤炭学报,2024,49(S1):22−35. TANG Yuesong, SUN Wenchao, LI Zengqiang, et al. Mechanism of mining stress surge and fall in filling mining face of rock burst mine[J]. Journal of China Coal Society,2024,49(S1):22−35.
[26] 何满潮,高玉兵,盖秋凯,等. 无煤柱自成巷力学原理及其工法[J]. 煤炭科学技术,2023,51(1):19−30. HE Manchao, GAO Yubing, GAI Qiukai, et al. Mechanical principle and mining methods of automagical entry formation without coal pillars[J]. Coal Science and Technology,2023,51(1):19−30.
[27] 高玉兵,杨军,王琦,等. 无煤柱自成巷预裂切顶机理及其对矿压显现的影响[J]. 煤炭学报,2019,44(11):3349−3359. GAO Yubing, YANG Jun, WANG Qi, et al. Mechanism of roof presplitting in a nonpillar mining method with entry automatically retained and its influence on the strata behaviors[J]. Journal of China Coal Society,2019,44(11):3349−3359.
[28] 姜礼尚,陈亚浙. 数学物理方程讲义[M]. 北京:高等教育出版社,1986. [29] 罗迎社. 材料力学[M]. 北京:高等教育出版社,2013.
下载:
