Study on the damage pattern of the cemented backfill at the jagged rock-fill interface under dynamic loading of blasting
-
摘要:
地下矿山采矿和充填作业过程中形成的胶结充填体在爆破动载作用下的损伤失稳与岩−充界面形态有直接关系。以往研究常将岩−充界面简化为平面状，但根据采场空区探测结果，岩−充界面往往具有锯齿状特征。运用连续介质理论和有限差分法数值模拟软件，建立了3种不同形态的锯齿状岩−充界面胶结充填体模型为实验组，1种平直状岩−充界面胶结充填体模型为对照组；推导岩体爆破等效腔腔壁上的爆炸荷载，并将其添加到数值模型中以模拟二步骤采场边孔爆破；结合充填体破坏损伤判据，研究了爆破动载作用下胶结充填体动力损伤响应，获得了岩−充界面锯齿宽度SW、灰砂比CSR、孔边距SHD、垂直应力σh等因素对充填体损伤范围和破坏模式的影响规律。结果表明：平面状岩−充界面下胶结充填体的损伤区域形状近似于矩形，而锯齿状岩−充界面的锯齿宽度越大，胶结充填体的损伤区域形状越接近菱形，更易发生楔形破坏；当σh相近时，对于CSR不同的两层相邻胶结充填层，CSR越大，充填体各质点的峰值振动速度衰减越慢，损伤区域面积也随之越大，相邻两层充填体之间越容易因振动速度不一致而诱发层间错动；当CSR相同时，σh越大，损伤区域面积越小。此外，胶结充填体的损伤区域面积与SHD呈明显负相关。在工程实践中，当边孔药量不可减小时，应选择合理的SHD以维持胶结充填体矿柱稳定。
Abstract:The morphology of the rock-fill interface, formed during mining and filling operations in underground mines, is directly related to the destabilization and damage of the cemented backfill under dynamic blasting loads. Previous studies often simplify the rock-fill interface to a planar shape; however, exploration results of empty areas in the quarry often characterize the rock-fill interface with jagged undulations. Applying continuum mechanics and numerical simulation software based on the finite difference method, three models of cemented backfill with different morphologies of serrated rock-fill interfaces were established as the experimental group, and one model with a flat and straight rock-fill interface was established as the control group; The time-history curve of the explosive load on the walls of equivalent cavities after rock blasting was derived and incorporated into a numerical model to simulate the two-step perimeter hole blasting in quarries. The dynamic damage response of cemented backfill under blasting loads was investigated by combining it with the backfill's damage criteria, and the influences of factors such as sawtooth width (SW) at the rock-fill interface, cement-sand ratio (CSR), side hole distance (SHD), vertical stress (σh), and others on the damage extent and mode were determined. The results show that: The damage area of the cemented backfill at a planar rock-fill interface resembles a rectangle, whereas at a jagged rock-fill interface with larger sawtooth widths, the damage area tends to approximate a rhombus, making it more prone to wedge-shaped damage; When vertical stress (σh) is similar, between two adjacent cemented backfill layers with differing CSR, the layer with the higher CSR exhibits slower attenuation of the peak vibration velocity at each mass point, resulting in a larger damage area and an increased likelihood of interlayer misalignment due to inconsistent vibration velocities; With the CSR constant, a larger σh results in a smaller damage area; Furthermore, the damage area of the cemented backfill is inversely correlated with SHD, and in engineering practice, selecting a reasonable SHD is crucial to maintaining the stability of the cemented backfill when the quantity of explosives for side holes cannot be reduced.
-
Keywords:
- blasting dynamic load /
- cemented backfill /
- rock-fill interface /
- dynamic response /
- damage
-
0. 引 言
近年来，随着世界范围内对矿产资源需求的增加，地球浅部矿产资源储量逐渐减小，深部开采已成为国内外众多矿山可持续发展的必经之路[1-2]。充填采矿法因其具有控制采场地压，减少围岩破坏，矿石损失贫化低等优点，已成为未来深部资源安全高效开采的主要方法[3-4]。其中，阶段空场嗣后充填采矿法更已成为厚大矿体开采的首选。但这种采矿方法采用了大直径深孔爆破的崩矿方式，其大药量设计在释放产能和保障矿石破碎效果的同时，约70～80%炸药能量经爆炸空腔、粉碎区和裂隙区后转化为强烈的弹性振动，进而易导致相邻胶结充填体发生片落、断裂、坍塌而造成贫化损伤，甚至引发整体垮落风险[5–8]。
国内外众多学者针对爆破作用下充填体的损伤失稳规律做了大量研究。TAN等[9]通过SHPB试验装置对不同灰砂比和固体颗粒含量的尾砂胶结充填试件进行冲击试验，分析了试件的应力应变特征关系、动态强度特征和动态破坏特征。LIU等[10]对含节理面的充填体试件进行SHPB冲击试验，利用高速摄影机和电镜扫描仪，分析了含充填节理面的充填试件在动态冲击下的破坏机理。CAO等[11]研究了动态冲击下充填体试件动态峰值抗压强度与平均应变率、灰砂比、养护龄期的关系，并通过数值分析验证了试验结果，认为动态峰值抗压强度随平均应变率的增大而增大。谭玉叶等[12]运用SHPB实验装置对循环冲击下充填体试件进行分析，探索了充填体不发生宏观破坏下循环冲击的应力−应变、动载强度和变形破坏特征，认为循环冲击有利于提高充填体破坏时的动载强度及整体承载能力。姜立春等[13]构建了充填体多自由度结构响应方法，对分层胶结充填体的动力响应机制进行分析，并结合数值模拟和现场监测结果进行验证，结果表明远场爆破水平应力波的频率对充填体的速度、位移响应情况有显著影响。黄欣成等[14]分析了爆炸应力波在充填体中的传播及其岩−充界面的相互作用规律，提出了不同灰砂比充填体的破坏模式和对应的质点振速阈值。朱鹏瑞等[15]建立了爆破动载下充填体的张拉破坏理论模型，分析了频繁爆破扰动对充填体的破坏机制。SUAZO等[16]运用LS-DYNA，分析了起爆顺序、爆破次数等因素对充填体孔隙压力的影响。EMAD等[17-18]利用 FLAC3D模拟了爆破过程，分析了充填体的稳定性；通过对充填体爆破振动进行监测和数据处理，在校准数值模型的基础上讨论了充填体破坏机理，并对动载下充填体稳定性进行评价。LI等[19]通过数值模拟方法研究了爆破方案与灰砂比对相邻充填体的影响，并通过巴西劈裂法和单轴压缩试验对试件的参数进行标定，发现同时起爆对充填体影响较小。胡建华等[20]运用LS-DYNA分析了爆破动载下岩−充界面耦合体模型的力学特征，获取了不同界面粗糙度、养护龄期和起爆方式等对充填体裂隙扩展和应力峰值的影响。
在上述研究中，为了便于探究充填体整体损伤失稳规律，大多将岩−充界面简化为平面。实际上，在未充填前，一步骤采场边孔爆破时就已经形成了类似锯齿状的临空面，由此导致二步骤采场开采时，岩−充界面形态为具有一定规律的锯齿状。锯齿状岩−充界面的锯齿宽度将改变爆炸应力波的入射角、频率、幅值、波速等，进而影响爆炸应力波的传播规律以及充填体的损伤区域范围[21-22]。
基于此，笔者运用有限差分法数值模拟方法，分别构建了1种平面状岩−充界面充填体数值模型作为对照组，3种锯齿状岩−充界面的充填体模型作为实验组，基于等效腔理论对二步骤采场边孔施加爆破动载，分析岩−充界面锯齿宽度SW、灰砂比CSR、孔边距SHD、垂直应力σh等因素影响下，爆破动载对充填体的损伤范围和破坏模式的影响。本文研究可为地下金属矿开采过程中形成的不同形态岩−充界面胶结充填体在爆破动载下的稳定性控制技术提供必要的理论依据，这对我国地下矿山岩体爆破施工及安全控制具有重要意义。
1. 工程背景
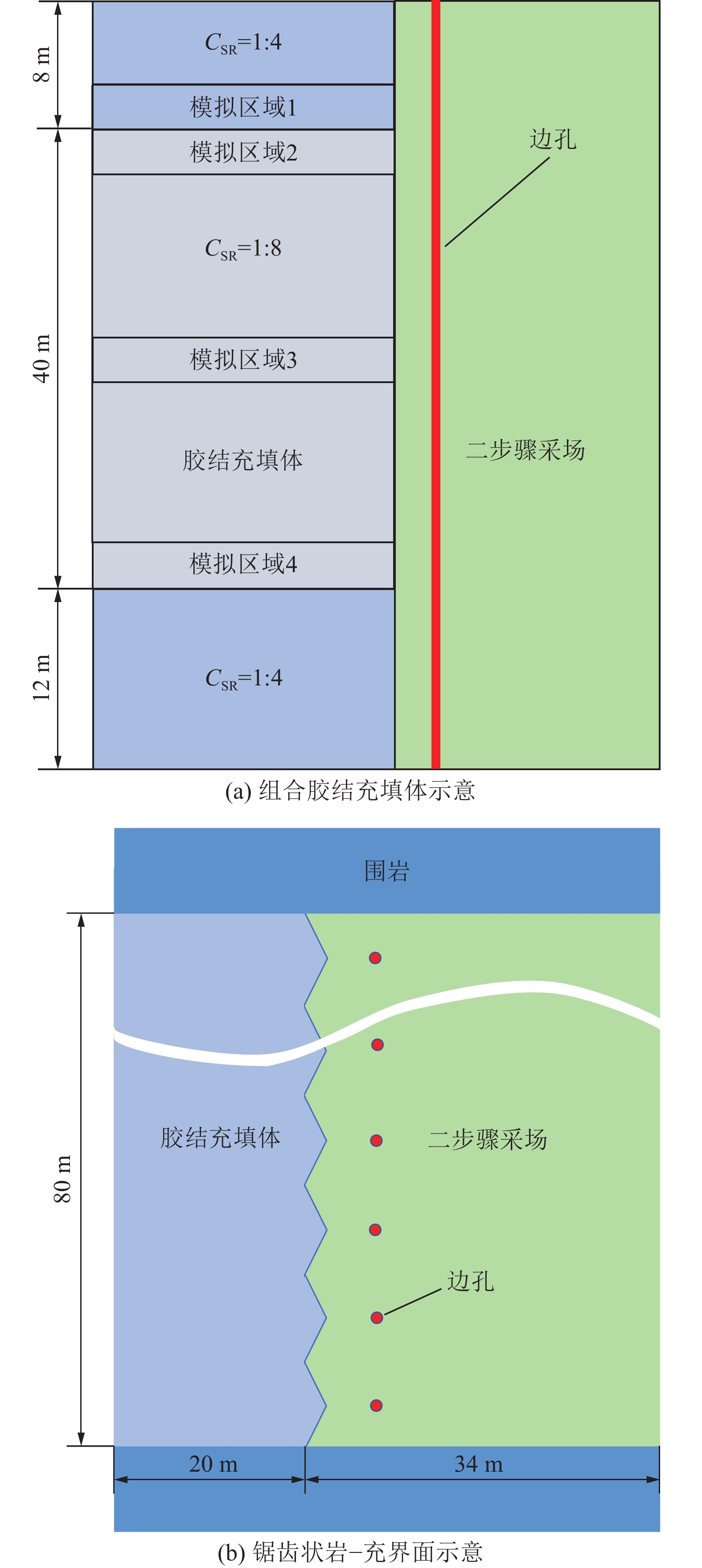
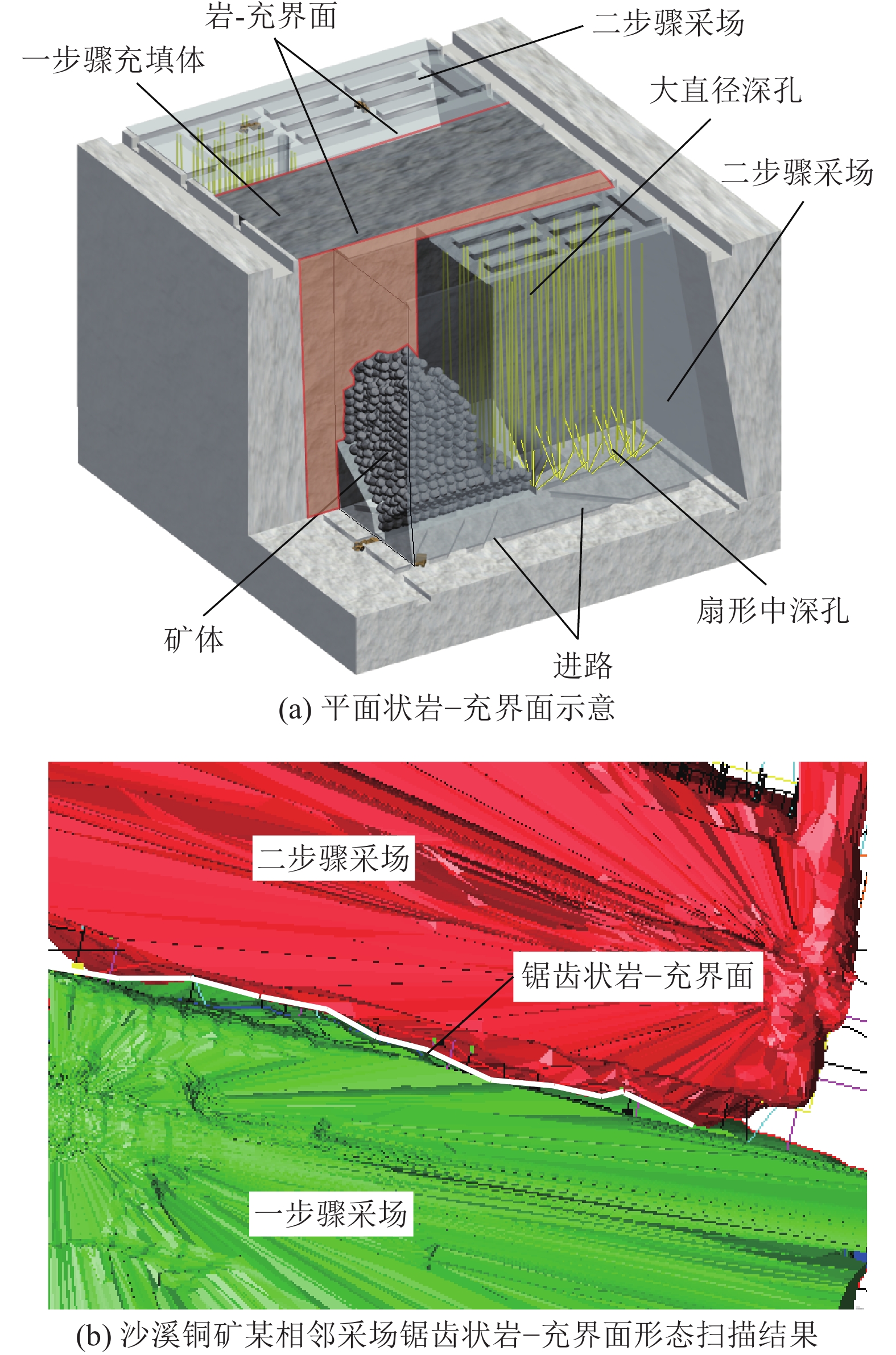
沙溪铜矿共有铜泉山、凤台山两个矿段，矿体埋藏深度、延度极大，属于典型的厚大低品位矿体。矿山采用大直径深孔阶段空场嗣后充填采矿法开采矿体，如图1a所示。其中一步骤采场结构参数为80 m×20 m×60 m(长×宽×高)，二步骤采场结构参数为80 m×34 m×60 m(长×宽×高)。图1b所示为沙溪铜矿某大直径深孔采场爆后与相邻充填体间岩−充界面形态的扫描结果，经分析，岩−充界面锯齿宽度在0～0.5 m范围内，这证明了岩−充界面起伏形态类似于锯齿状。
以沙溪铜矿铜泉山矿段的T101、T102采场为例，T101采场为一步骤采场，T102采场为二步骤采场。T102采场大孔孔径为110 mm，排间距为1.8～2.2 m，孔间距为2.0～2.2 m。其中，为控制边帮爆破效果，SHD设计约为1～1.5 m，采用直径dc=90 mm的乳化炸药，炸药密度ρ0为
1300 kg/m3；炸药爆速D为4600 m/s。采场开采起爆顺序为：先起爆拉槽区，之后以槽区为自由面和补偿空间进行侧向崩矿。一步骤采场采用CSR为1∶4和1∶8的全尾胶结砂料浆组合充填，如图2a所示，第一层和第三层CSR均为1∶4，中间第二层CSR为1∶8，二步骤采场采用全尾砂非胶结充填。该矿山矿体与岩体物理力学参数见表1，全尾砂胶结充填体物理力学参数见表2。一步骤采场开采时，边孔的爆炸冲击波沿径向扩散传播，在很短的距离内，爆炸冲击波衰减为应力波，不再能够使得岩体破裂。在理想情况下，边孔爆破后，一步骤采场和二步骤采场的交界面近似为不规则锯齿状，为了数值模拟分析时网格划分合理，以及有效模拟边孔爆破荷载的传递，将波浪形岩−充界面简化为规则锯齿状界面，如图2b所示。
表 1 矿体、岩体物理力学参数Table 1. Mechanical properties of orebody and rock名称 密度
ρ/(kg·m−3)泊松比
μm内摩擦角
Φm/(°)黏聚力
cm/MPa弹性模量
Em/GPa抗压强度
σc/MPa抗拉强度
σmt/MPa围岩 2700 0.30 41.45 3.64 34.64 74.7 3.22 矿体 2810 0.25 37.92 1.98 38.25 65.3 4.87 表 2 胶结充填体物理力学参数Table 2. Mechanical properties of backfill灰砂比 密度
ρ/(kg·m−3)泊松比
μ内摩擦角
Φ/(°)粘聚力
c/MPa弹性模量
E/MPa抗压强度
σc/MPa抗拉强度
σt/MPa动态抗拉强度
σtd/MPa1:4 1712 0.28 32.4 1.39 274 1.64 0.32 0.41 1:8 1730 0.29 29.8 0.40 116 1.26 0.12 0.18 2. 数值模拟
2.1 数值模型与模拟方案
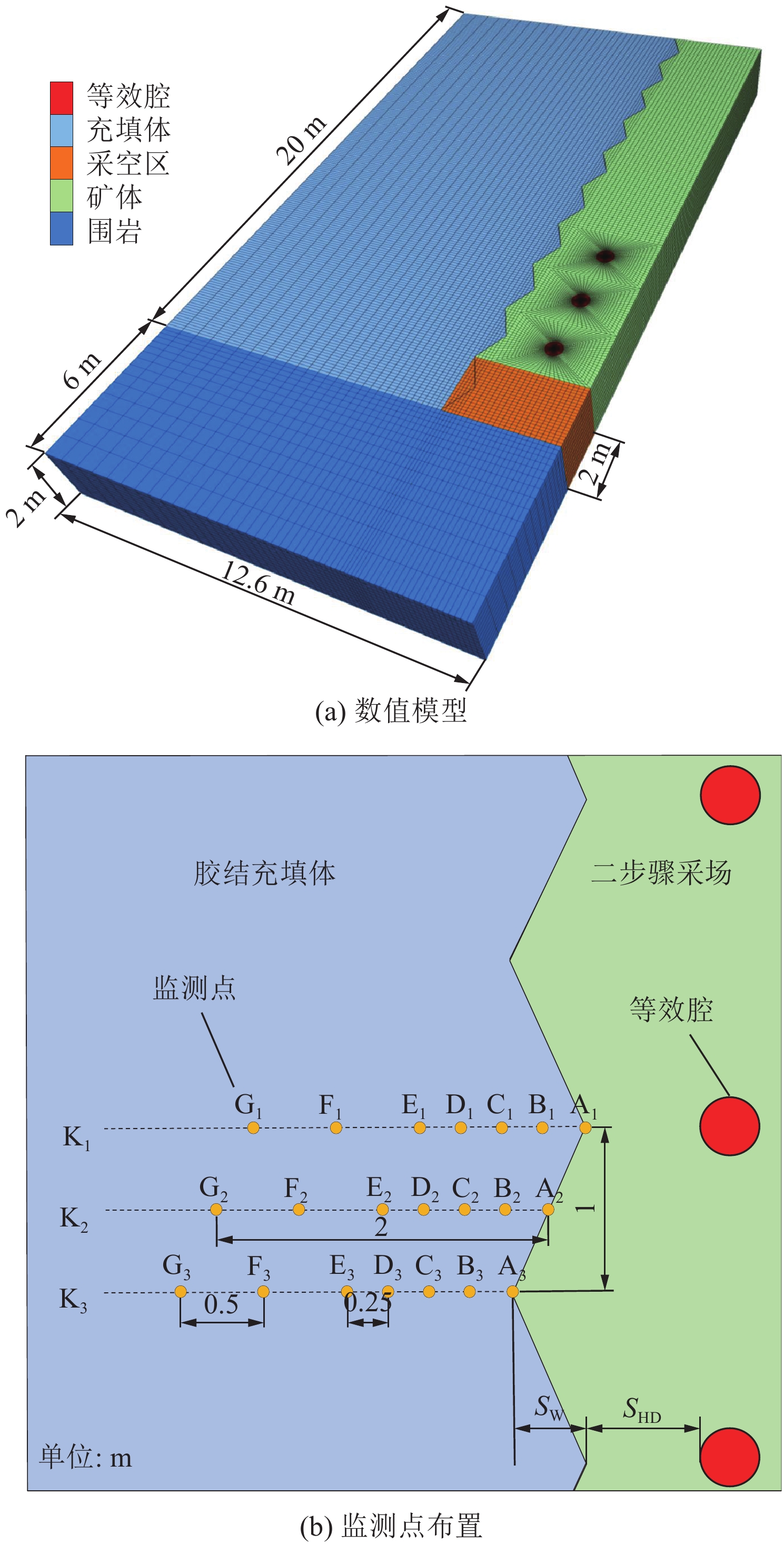
二步骤矿体开采时，边孔爆破冲击常引发充填体边帮垮落失稳。一步骤采场充填结束后无法再进入，且二步骤采场回采时顶板边帮有垮落风险。考虑到安全和成本问题，相关振动监测仪器很难安设在充填体内，且充填体边孔爆破产生的强烈振动容易引起监测仪器数据失真，难以用监测仪器在现场获取充填体损伤失稳情况。因此，本文根据图2所示矿体−充填体−围岩体系，在FLAC3D中建立如图3a的充填体数值模型，分析组合胶结充填体在边孔爆破动载作用下的损伤情况。其中，充填体、矿体和围岩均采用摩尔−库伦本构模型，等效腔和采空区的本构模型均采用空模型。尾砂胶结充填时因需要排水，导致组合胶结充填体难以结顶，养护结束后在垂直方向上仅承受组合胶结充填体的自重，因此，假设模型顶部不受地压作用。
为了减小模型尺寸和网格数量，增大研究区域的网格密度以提高计算效率和准确性，通过改变充填体数值模型所受到的垂直压力和不同灰砂比条件下的充填体物理力学参数，即可模拟计算不同高度方向上各模拟区域的动力响应情况。在相同高度方向上，水平侧压可假设为一致，σh等于单位面积上所覆盖的充填体的重量，即
$$ {\mathrm{\sigma }}_{\mathrm{h}}=\mathrm{\rho }\text{g}H $$ (1) 式中：σh为垂直压力，MPa；ρ为充填体密度，kg/m3；g为重力系数，取9.80 N/kg；H为上覆充填体的高度，m。
由此探究典型模拟区域1～区域4在不同SW、CSR、SHD、σh工况下的动力响应情况。岩−充边界上各点与等效腔之间的距离不同，爆炸应力波的叠加程度不同，导致胶结充填体的最大损伤长度L也不同。中间等效腔的爆炸应力波作用区域受上下两个等效腔的影响，因此，在中间等效腔附近，沿岩−充边界布置三条监测线，分别为K1、K2、K3，每条监测线上等距布置7个监测点，序号按照顺序依次标记为A～G，如图3b所示。
2.2 等效爆炸荷载
炸药起爆后，将在炮孔周围形成粉碎区，裂隙区和弹性振动区，粉碎区内的岩体不再是弹性体，且不具有连续性，而FLAC3D作为连续介质理论分析软件，不适用于重现炸药爆炸后粉碎区岩体的一系列复杂力学过程。基于此，为了更好地模拟边孔爆破对充填体的影响，在爆破区域内，用柱状等效腔代替柱状边孔，将爆破荷载添加到柱状等效腔壁面上。该方法在模拟爆破对岩体的损伤破坏效应时常被运用[23–26]。在以往研究中，常以粉碎区直径作为等效腔直径[27-28]；但由于岩性和炸药性质的差异，国内外学者经研究后，认为粉碎区直径一般为炮孔直径的3～5倍[29-30]。因此，笔者设定等效腔的直径为5倍炮孔直径[31]，即550 mm。
对于相邻2个采场，穿脉巷道掘进完毕后，在采场长度方向上2个采场交界区域内的矿体长度参数已经固定，以沙溪铜矿为例，其一、二步骤采场长度均为80 m。因采矿方法一致，采场在进行爆破设计时，相邻两个采场的边孔孔网参数相同，则两采场的边孔在长度方向上的相对位置大致为平行状态。在此基础上，为了使爆炸应力波能量尽可能多地透射到充填体内，同时简化数值计算模型，最终设定等效腔中心位置与岩−充界面右侧齿间位置在同一直线上。
对于非耦合装药的圆柱形炮孔，炮孔壁上压力峰值P0计算公式[32]为
$$ {P_0} = K\frac{{{\rho _0}{D^2}}}{{2\left( {1 + \beta } \right)}}{\left( {\frac{{{d_{{\mathrm{c}}}}}}{{{d_{{\mathrm{b}}}}}}} \right)^{2\beta }} $$ (2) 式中：ρ0为炸药密度，kg/m3；D为炸药爆速，m/s；β为炸药的绝热指数，无量纲；dc、db分别为药卷直径和炮孔直径，mm；K为压力增大倍数，一般取K=8～11。
由于等效腔建立在粉碎区的边界上(5倍炮孔直径边界处)，因此式(2)不能作为爆炸载荷输入到等效腔壁上，需求解等效腔腔壁上的爆炸荷载曲线。根据单个炮孔周围的爆炸载荷随距离衰减的规律[33]：
$$ {P_{\left( t \right)}} = {P_{\left( {x,t} \right)}}{\left( {\frac{{{r_0}}}{{{r_1}}}} \right)^\alpha } $$ (3) 式中：P(t)为随距离衰减的爆炸载荷，MPa；r0为炮孔半径，mm；r1为粉碎区半径，mm；α为应力波衰减指数，无量纲，在粉碎区内，对于爆炸冲击波，α=2+μ/(1-μ)，μ为岩石泊松比。P(x,t)为任意距离截面上的爆破载荷，可由下式给出[34-35]：
$$ {P_{\left( {x{\text{,}}t} \right)}} = {P_{{\mathrm{VN}}}}{\left( {{{e\gamma } \mathord{\left/ {\vphantom {{e\gamma } n}} \right. } n}} \right)^n}{H_{\left( t \right)}}{t^n}{{\mathrm{e}}^{ - \gamma t}} $$ (4) 式中：PVN是炸药产生的爆炸前沿的峰值压力，在爆破初始阶段，爆炸压力直接作用于炮孔壁上，因此对于柱状非耦合装药，可由式(2)中P0表示PVN ，H(t)是Heaviside单位阶跃函数，n为整数，γ为压力衰减系数，t为时间，s。其中H=1，n=3，γ=0.7[36]。
结合式(2)—式(4)，可以得出，在等效腔模型中，施加到等效腔壁上的爆破荷载表达式为
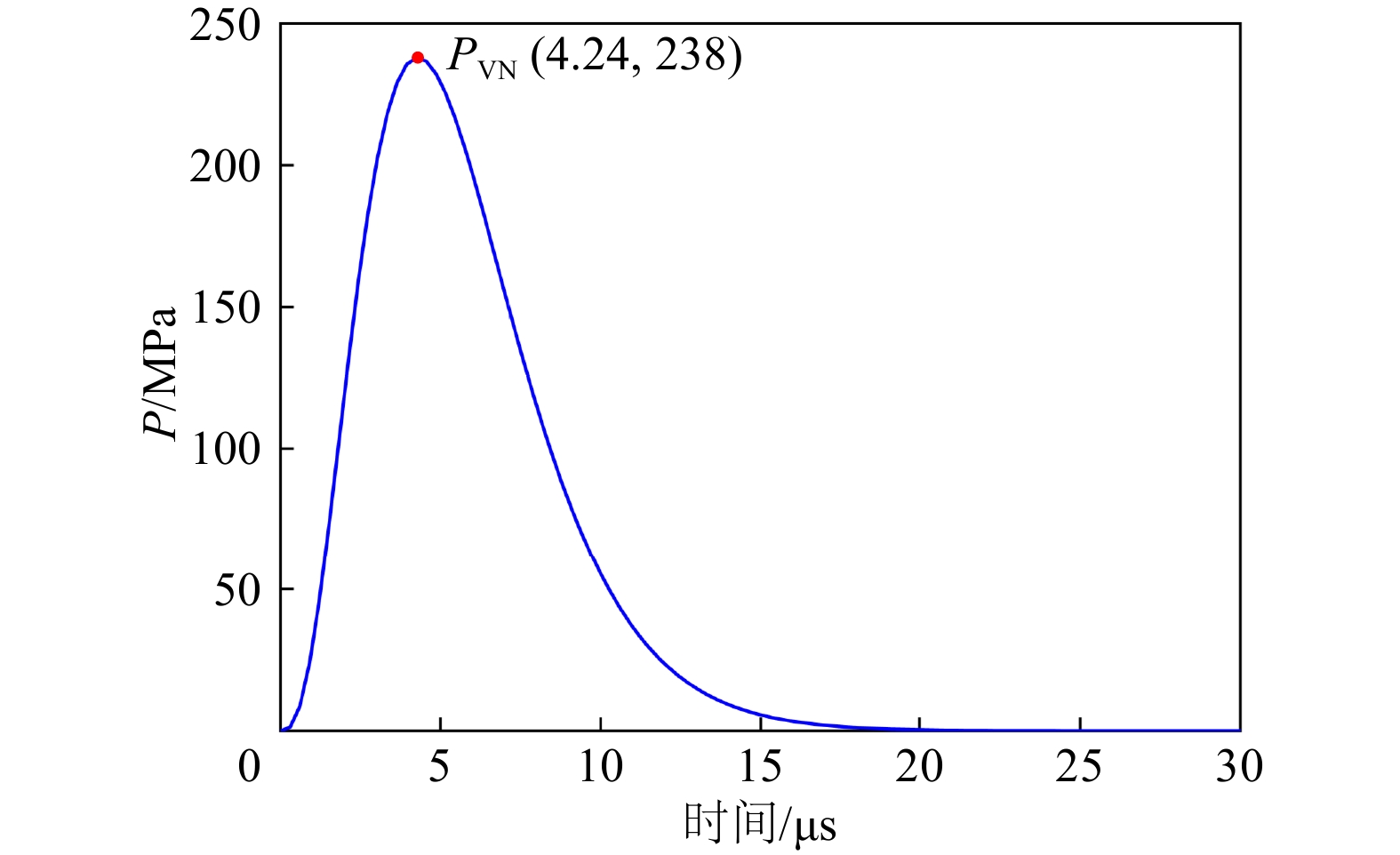
$$ {P_0} = K\frac{{{\rho _0}{D^2}}}{{2\left( {1 + \beta } \right)}}{\left( {\frac{{{d_{\mathrm{c}}}}}{{{d_{\mathrm{b}}}}}} \right)^{2\beta }}{\left( {{{e\gamma } \mathord{\left/ {\vphantom {{e\gamma } n}} \right. } n}} \right)^n}{H_{\left( t \right)}}{t^n}{{\mathrm{e}}^{ - \gamma t}}{\left( {\frac{{{r_0}}}{{{r_1}}}} \right)^\alpha } $$ (5) 根据T102采场矿体物理力学参数和边孔采用的炸药的属性，D=
4600 m/s，ρ0=1300 kg/m3，dc=90 mm，db=110 mm，K=10，β=3.0，γ=0.7，α=3，r0=55 mm，r1=275 mm。将各参数详细取值代入式(5)，可得到在数值模型等效腔上施加的爆破荷载时程曲线，如图4所示，施加在等效腔壁上的爆破荷载峰值压力PVN为238 MPa，持续时间约为21 us。2.3 动力阻尼和边界条件
在工程实际中，岩体材料受到外力冲击时，材料内部的摩擦以及原生、次生微裂纹和裂隙之间存在的滑动将导致能量损失。在FLAC3D模拟中，常通过设置阻尼的方式来复现岩体在外力荷载作用下的能量损失，但局部阻尼只适合简单问题的求解，并不能有效地衰减复杂波形的高频部分[37]。因此，本文选用能减弱系统自然振动的瑞利阻尼。对于岩土类材料而言，临界阻尼比在2%～5%范围内，本文选取4%；最小中心频率通过对模型进行无阻尼自振计算，求得其值为18.38 Hz[38]。
爆破载荷输入到等效腔上后，爆炸应力波传播到模型边界时将会发生反射，使模型受到二次扰动，因此，需要设置边界条件来减少模型边界上爆炸应力波的反射。在本文数值模型中，爆破荷载入射波在胶结充填体和矿体边界上的入射角均大于30°，因此，边界条件设置静态边界，一方面能达到完全吸收爆炸应力波的目的，另一方面，在不影响分析结果的前提下还可以缩小数值模型的尺寸，减轻计算负担。
3. 模拟结果分析
3.1 胶结充填体振动安全判据
根据弹性应力波理论，岩石的物理力学参数与其声学特性有关，进而可建立岩体的动态应力与质点振动速度的关系[39-40]，如下
$$ \left\{ \begin{gathered} V = {{{\sigma _{{{\mathrm{td}}}}}} \mathord{\left/ {\vphantom {{{\sigma _{{{\mathrm{td}}}}}} {\left( {\rho {c_1}} \right)}}} \right. } {\left( {\rho {c_1}} \right)}} \\ \eta = 1 - {{{c_1}} \mathord{\left/ {\vphantom {{{c_1}} {{c_0}}}} \right. } {{c_0}}} \\ \end{gathered} \right. $$ (6) 式中：V为胶结充填体内质点振动速度，cm/s；σtd为胶结充填体动态抗拉强度，MPa；η为爆破作用前、后声速降低率，工程实践中一般取η=10%；ρ为胶结充填体密度，kg/m3；c0、c1分别为岩体在爆破前、后的纵波波速，m/s。
假定岩体为均质、各向同性体，根据岩体物理力学参数，岩石的爆破前的纵波波速c0将容易求解，进而将动态抗拉强度作为胶结充填体在爆破动载作用下的破坏标准，可得到胶结充填体振速安全阈值判据如下：
$$ {V_{\max }} = \frac{{{\sigma _{{{\mathrm{td}}}}}}}{{0.9\rho {c_0}}} = \frac{{{\sigma _{{{\mathrm{td}}}}}}}{{0.9\sqrt {\dfrac{{\rho E\left( {1 - \mu } \right)}}{{\left( {1 + \mu } \right)\left( {1 - 2\mu } \right)}}} }} $$ (7) 将表1、表2中的物理力学参数代入式(7)，可得到CSR分别为1∶4和1∶8的胶结充填体振速安全阈值Vmax分别为29.3和17.1 cm/s。以Vmax为判据，针对组合胶结充填体在SW、CSR、SHD、σh等因素影响下，受爆破动载作用时产生的损伤情况进行分析。
3.2 不同锯齿宽度岩−充界面对胶结充填体损伤的影响
如前文所述，锯齿宽度SW的大小与矿体物理力学性质和一步骤矿房回采爆破作业相关，特别是一步骤采场回采时的孔边距、边孔装药量、孔网参数等因素。针对于本文研究的组合胶结充填体，灰砂比CSR为1:8的充填体占整个组合胶结充填体的66.67%，因此，本节针对CSR=1∶8，σh=0.15 MPa，SHD =1.2 m的胶结充填体，讨论SW分别为0、30、40、50 cm工况下，胶结充填体在爆破动载下的损伤情况，工况方案如表3所示，相对应的数值模型位置为图2a中的模拟区域2，特别地，当SW=0 cm时，岩−充界面为平面状。
表 3 模拟锯齿宽度变化的工况方案Table 3. Working condition that simulate variations in the SW工况编号 模拟区域 CSR SW/cm SHD/m σh/MPa 工况1 区域2 1∶8 0 1.2 0.15 工况2 区域2 1∶8 30 1.2 0.15 工况3 区域2 1∶8 40 1.2 0.15 工况4 区域2 1∶8 50 1.2 0.15 3.2.1 不同锯齿宽度下各监测点振动速度变化
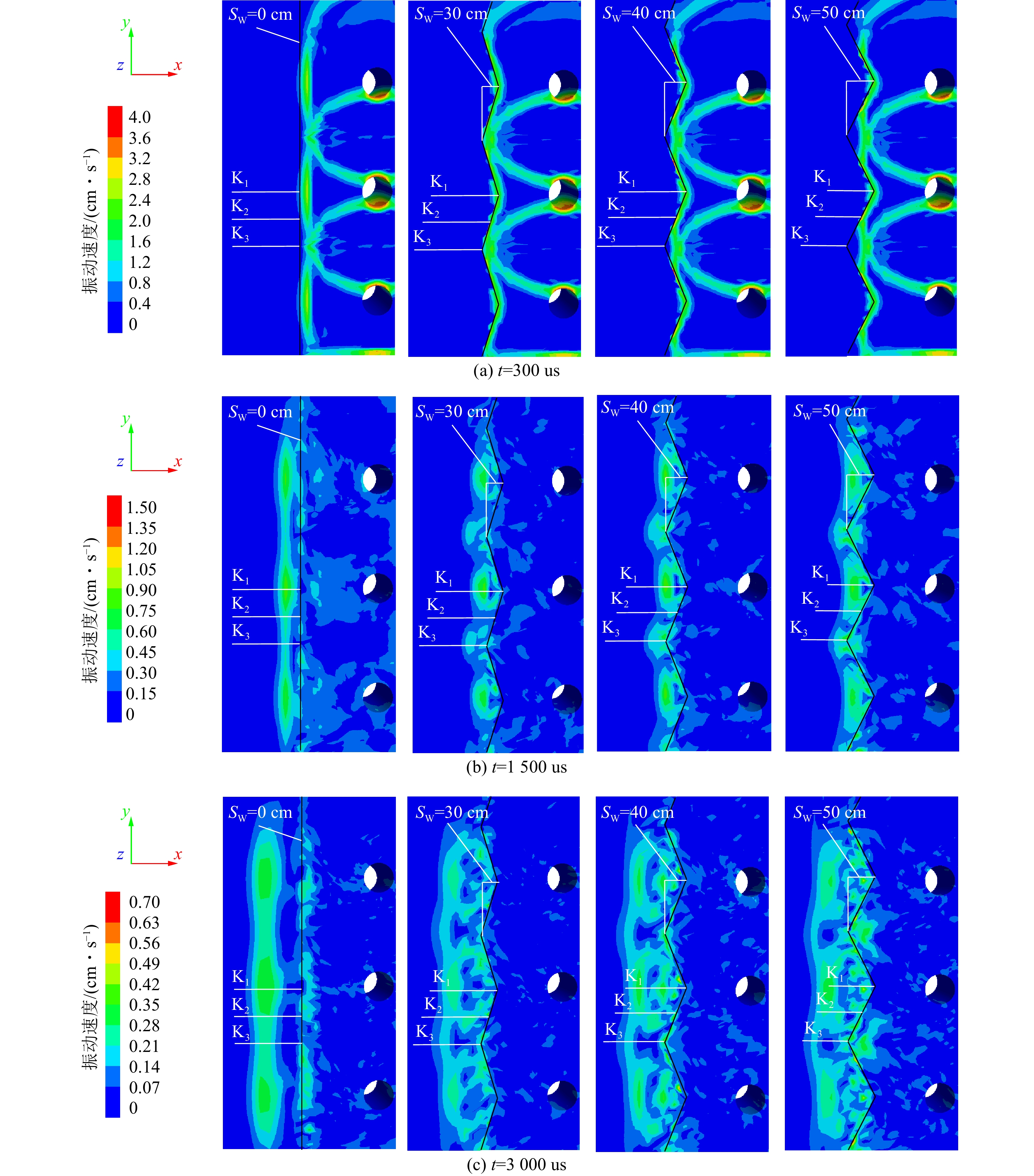
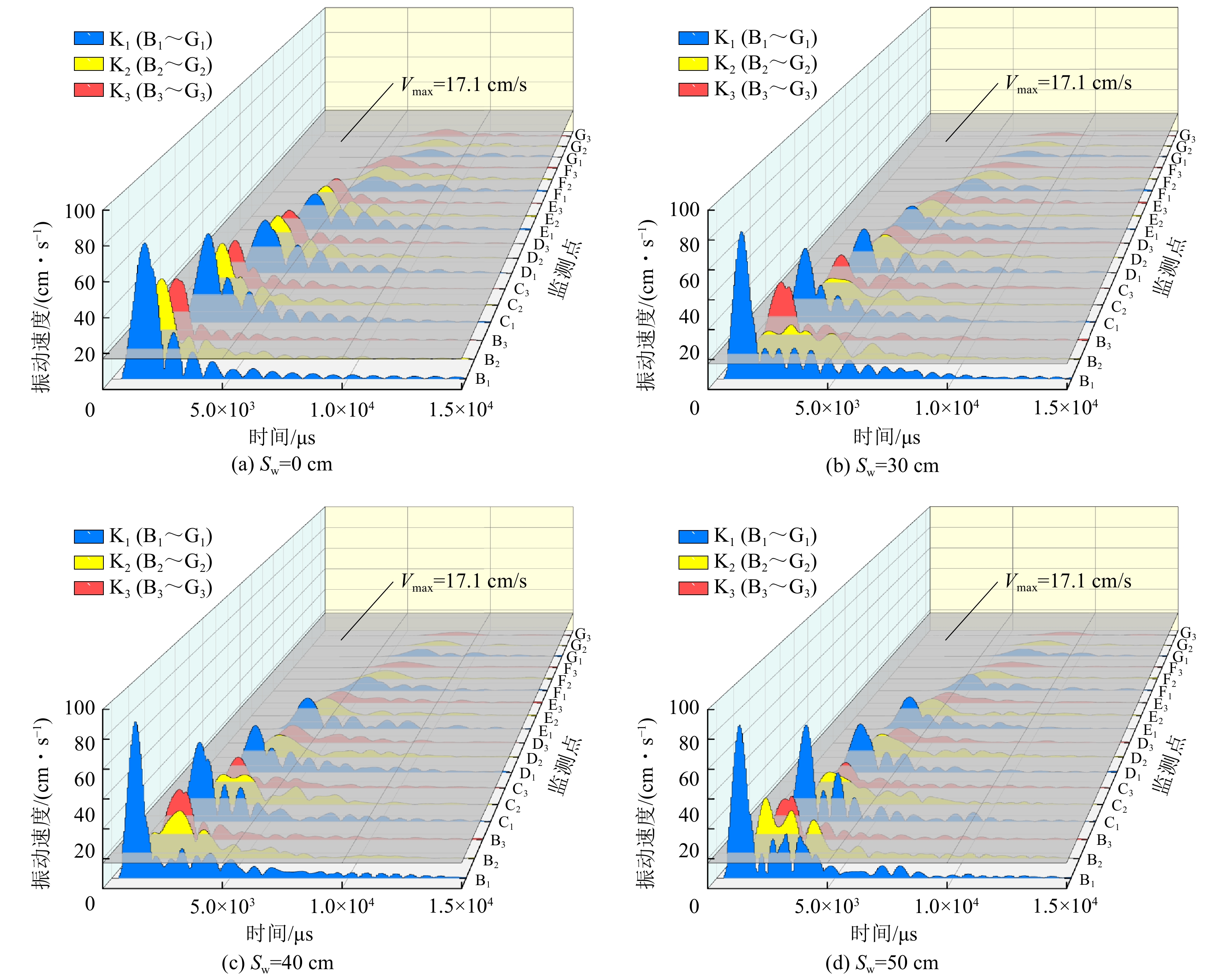
如图5显示了爆破动载下，SW分别为0、30、40、50 cm时胶结充填体模型在t=300、
1500 、3000 us这3个时刻的振动速度变化情况。![]()
图 5 不同锯齿宽度下胶结充填体的振动速度变化情况Figure 5. Variation of vibration velocity of backfill at the different SW从图5a中能明显看出，当SW=0 cm时，尽管K3监测线附近的岩−充界面在t=300 us时刻受到爆炸应力波叠加作用，相比K1附近区域，K3区域附近的胶结充填体振动速度反而更小。由图5b、图5c可知，当SW=0 cm时，随着爆炸应力波的传播，胶结充填体内K1区域的振动速度依旧比K3区域的更大。
与SW=0 cm情况类似，当SW=30、40、50 cm时，所有时刻内K1区域的振动速度比K3区域的振动速度大。但与SW=0 cm不同的是，锯齿状岩−充界面的存在使得爆炸应力波传播到充填体内后，K3监测线附近的质点总是超前于K1附近的质点产生振动，且锯齿宽度越大，充填体内振动速度相近的区域越趋于离散。
爆破动载施加
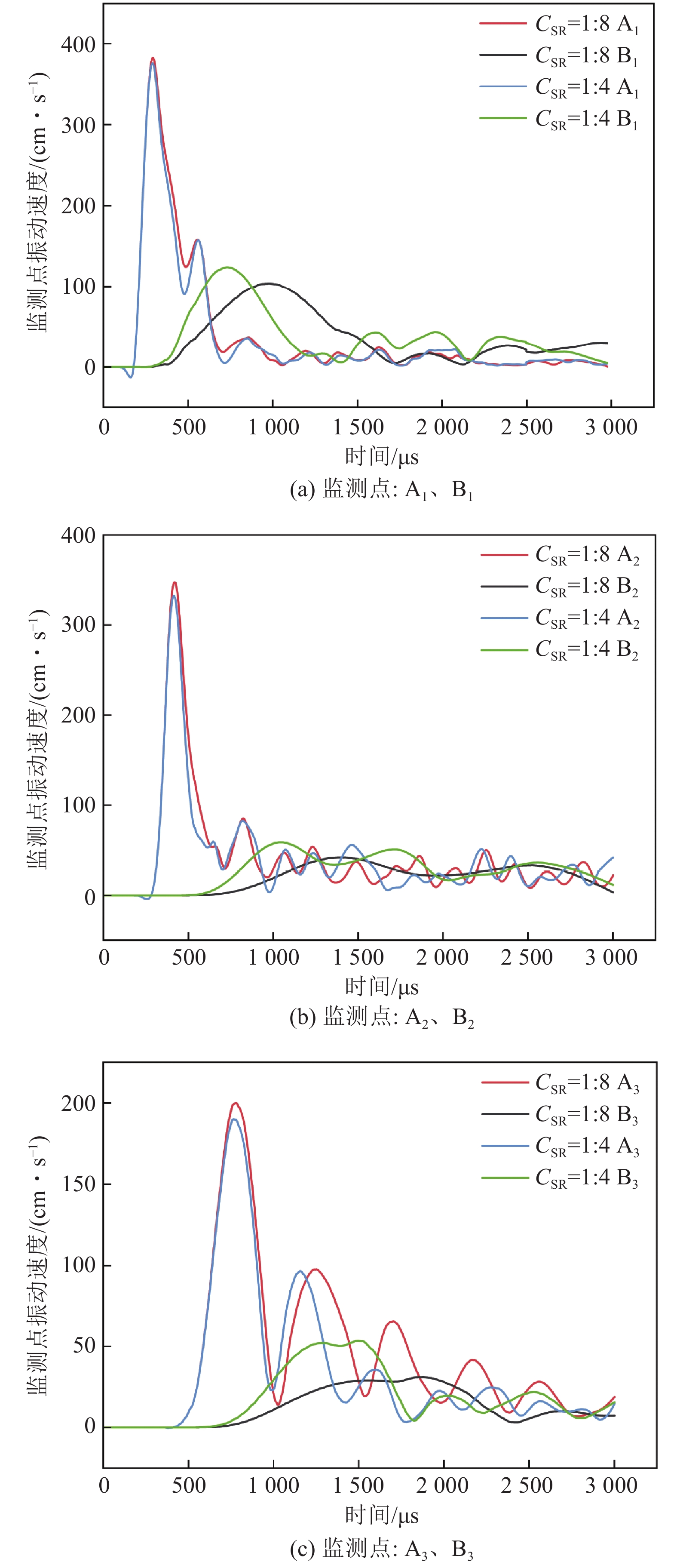
15000 us后，根据数值模型计算结果，分析K1(监测点B1～G1)、K2(监测点B2～G2)、K3(监测点B3～G3)等3列监测点的速度时程曲线，如图6所示，因岩−充界面上承受的爆破动载较大，则图6中未包括A1、A2、A3这3个监测点的振动速度变化。![]()
图 6 不同锯齿宽度时各监测点速度时程曲线Figure 6. Velocity time history curve of each monitoring point under the different SW从图6a可知，在相同工况下，当SW=0 cm时，共有12个监测点的峰值振动速度(PPV)超过安全值Vmax(17.1 cm/s)，距离岩−充界面最远发生破坏的监测点分别为E1、E2、E3。当SW=30、40、50 cm时，各个充填体模型中均有9个监测点超过PPV的安全值Vmax(17.1 cm/s)，距离岩−充界面最远的监测点均为K1列的E1监测点。值得注意的是，对于K1列和K3列的各监测点，其监测点振动速度随着时间变化而逐渐递减，而K2列的监测点受到爆炸应力波叠加影响，其振动速度变化更为复杂，导致振动周期规律性较差，例如B2。
此外，由图6b、6c、6d可知，当SW增大时，K1和K2列监测点的PPV随之增大；但SW变化引起叠加后的爆炸应力波入射角度不同，使K3列监测点的PPV反而随SW增大而减小。
3.2.2 不同锯齿宽度岩−充界面对胶结充填体损伤的影响
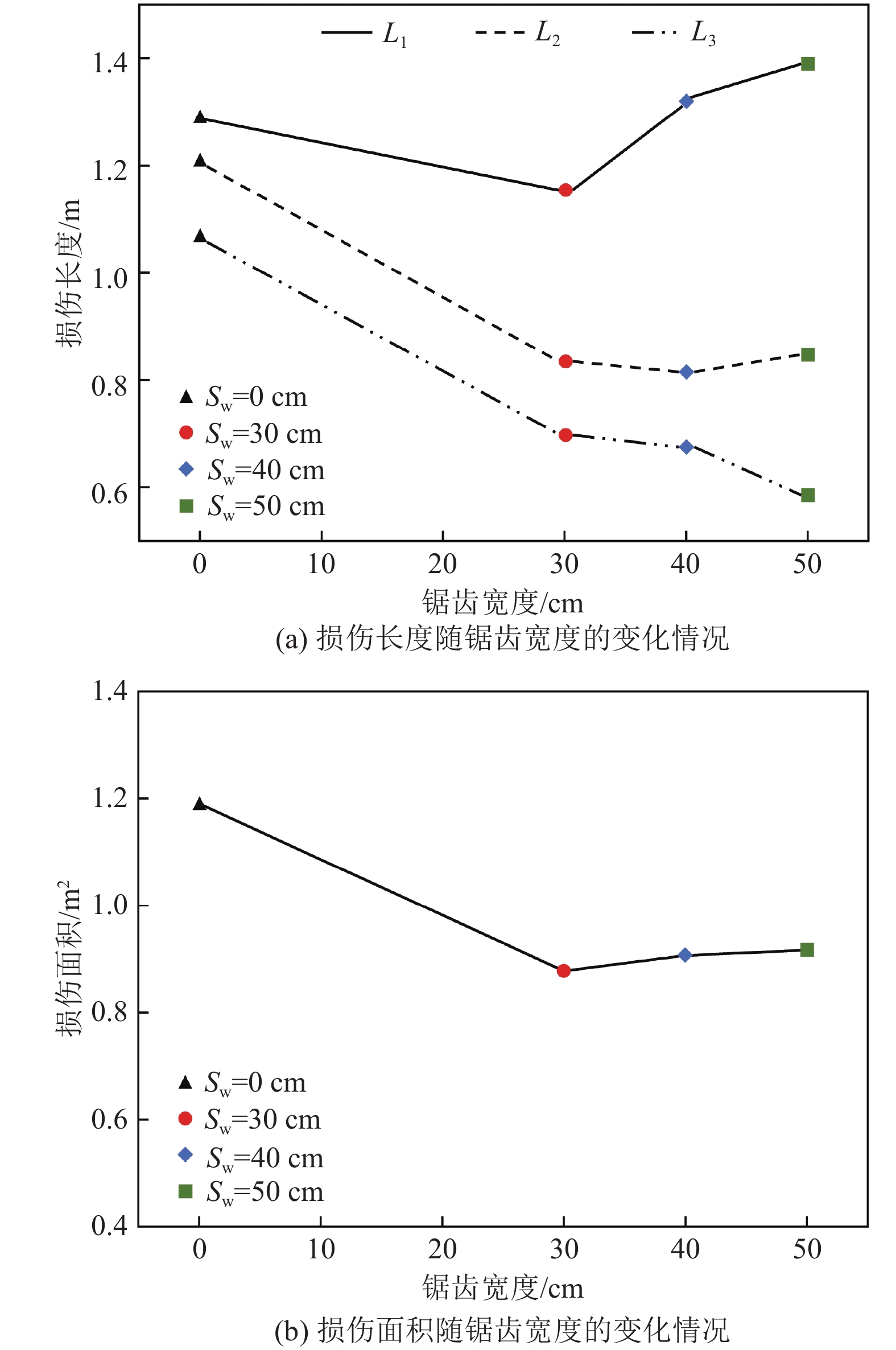
由以上可知，在相同爆破动载作用下，不同SW对胶结充填体的损伤区范围有显著影响，根据图6中各个胶结充填体模型监测线K1、K2、K3上的PPV，经过数据分析，提取出每列监测线上超过胶结充填体振速安全阈值Vmax(17.1 cm/s)且距岩−充界面最远处的坐标，最终得到不同SW下，胶结充填体模型中各列监测线方向上的最大损伤长度L，如图7a所示。
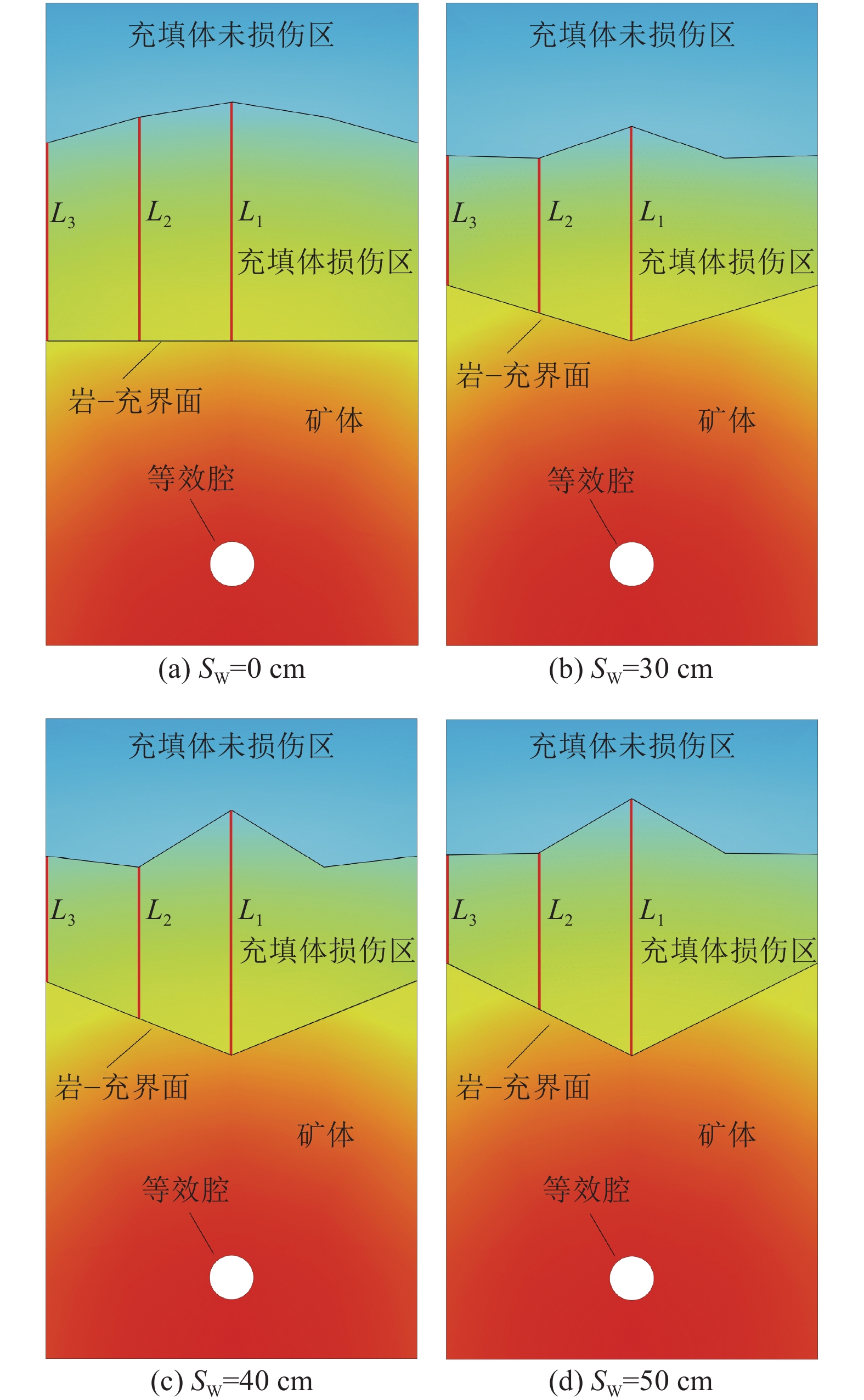
从图7a可知，不管V如何变化，K1监测线方向上的最大损伤长度L1最大，K2次之，K3监测线方向上的最大损伤长度L3最小。随SW的增大，K1、K2监测线方向上的L1、L2呈先减小后增大的趋势；K3监测线方向上L3随SW增大而减小。SW=0 cm时，最大损伤长度L1=1.29 m，最小损伤长度L3=1.06 m，二者差值为0.23 m，即胶结充填体在三列监测线方向上L较接近，胶结充填体损伤区域形状近似矩形状，如图8a所示；同一爆炸应力波斜射入岩−充界面时，随着SW的增大，同一爆炸应力波的入射角也增大，岩−充界面对爆炸应力波的衰减作用逐渐增强[41]。因此SW越大，K2、K3范围内的L越小，而相邻炮孔的应力波反射到K1范围内，导致K1范围内的L更大；当SW相同时，从相同位置开始传播的一组爆炸应力波，从锯齿尖部传入时的入射角小于从锯齿根部传入的入射角，因此锯齿尖部的爆炸应力波衰减得更少，同样导致K1方向的L更大。
计算出不同SW时的损伤面积S，如图7b所示，结合图7a可知，随着SW的增大，S呈现先减小后缓慢增大的趋势。S越大，单个锯齿范围内的充填体两端的L减小，中间部位L的增大，胶结充填体的损伤区域形状由近似矩形状向近似菱形状过渡，越容易发生楔形垮落，如图8b—图8d所示。
综上所述，对于更符合实际工况的锯齿状岩−充界面，随着锯齿宽度的增大，透射应力波的衰减程度逐渐增大。但充填体锯齿尖部区域内的应力波衰减速率大于锯齿根部，导致胶结充填体损伤区域形状类似菱形，极易发生楔形垮落。
3.3 灰砂比对不同锯齿宽度胶结充填体损伤的影响
为了探究不同灰砂比CSR对胶结充填体的影响，针对于本文研究的组合胶结充填体，选取SW=0、50 cm，SHD =1.2 m的数值模型，分别讨论V为1∶4(模拟区域1)、1∶8(模拟区域2)工况下，胶结充填体在爆破动载下的损伤情况，其对应承受的σh分别为0.12、0.15 MPa，在分析时可忽略σh不同而带来的影响，工况方案见表4。
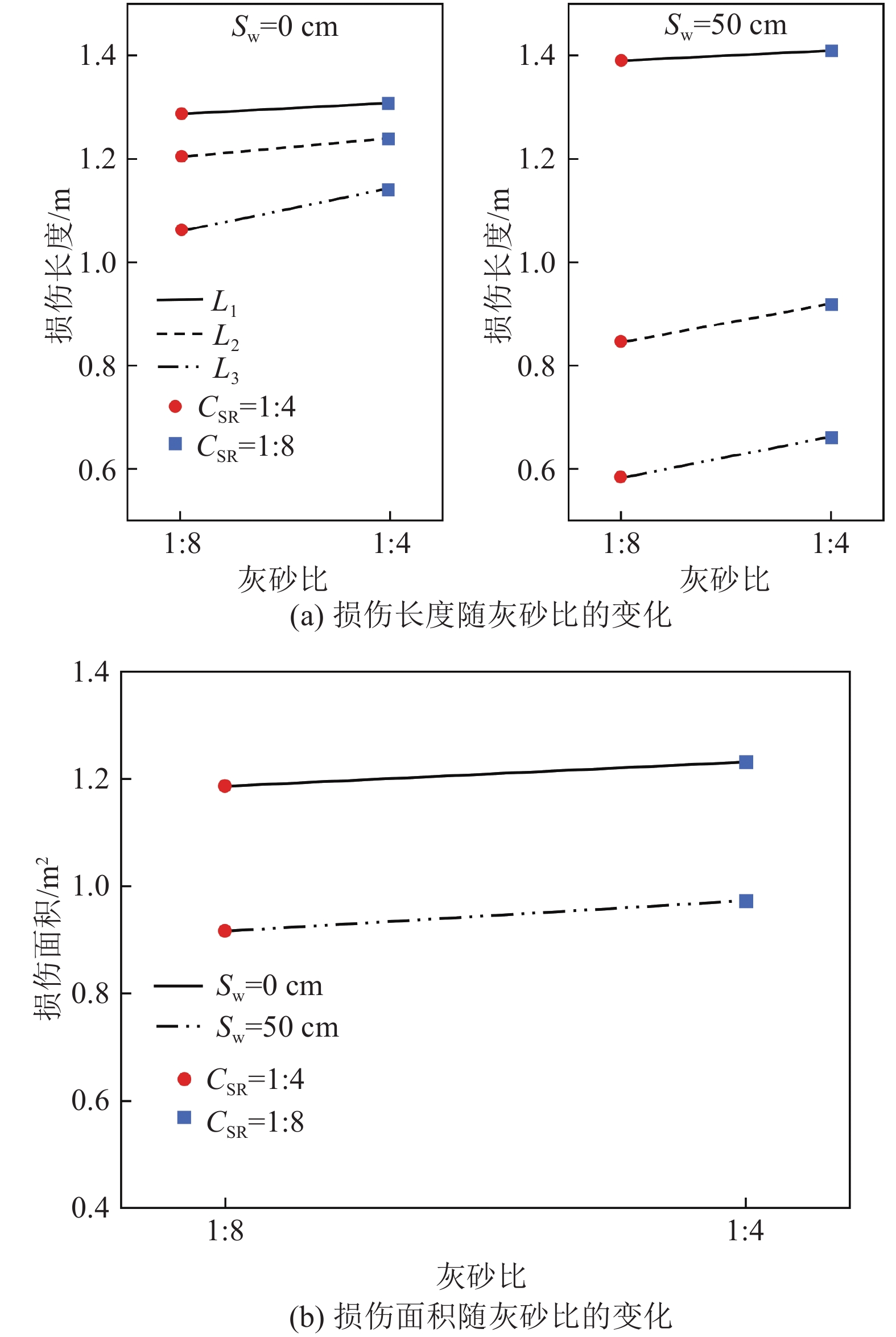
表 4 模拟灰砂比变化的工况方案Table 4. Working condition that simulate variations in the CSR工况编号 模拟区域 CSR SW/cm SHD/m σh/MPa 工况1 区域1 1∶4 0 1.2 0.12 工况2 区域2 1∶8 0 1.2 0.15 工况3 区域1 1∶4 50 1.2 0.12 工况4 区域2 1∶8 50 1.2 0.15 根据数值模拟计算结果所得到的胶结充填体模型K1、K2、K3三列监测线上的PPV，经过数据分析，提取出每列监测线上超过Vmax且距岩−充界面最远处的坐标，最终得到SW=0、50 cm情况下，不同CSR时组合胶结充填体模型中各列监测线的L，如图9a所示，损伤面积S如图9b所示。特别地，CSR为1∶4和1∶8时对应的Vmax分别为29.3和17.1 cm/s。
由图9a可知，当SW增大时，两种CSR下的充填体模型在K1监测线上的L均增大，K2、K3监测线方向上的L均减小。这同样符合3.2.3节中SW的增大将使得胶结充填体的损伤区域形状由近似矩形状向近似菱形状过渡的结论。相同SW下，随着CSR的增大，胶结充填体相同监测线方向上L逐渐增大，如SW=50 cm，CSR为1∶8时，K3方向上的最大损伤长度L3=0.58 m；CSR为1∶4时，L3=0.65 m。造成这种情况的原因在于，高灰砂比的胶结充填体波速更大，则对应波阻抗也越大。同一爆炸应力波在经岩−充界面传入胶结充填体内的过程中，胶结充填层的波阻抗越大，应力波反射越少，透射应力波的波能越多，应力波传播速度越快，且衰减越慢。最终导致当垂直应力相近时，高灰砂比充填体的最大损伤长度L更大[42-43]。
例如，在本节研究中，这两种CSR胶结充填体的垂直应力几乎相同，在相同的爆炸荷载和SW下，CSR为1∶4时胶结充填体模型内的应力波传播速度越快，各监测点振动速度达到峰值的耗时更短，且相邻监测点的振动速度峰值衰减得更慢。根据数值模型计算结果和各监测线上的L，得出不同CSR下，SW=0、50 cm时的S，如图9b所示。结合图9a、9b可知，SW相同时，S随着CSR的增大而缓慢增大；CSR相同时，S随SW增大而减小。
选取图3b中的A1、B1、A2、B2、A3、B3作为典型监测点进一步分析不同CSR下的速度衰减差异。当SW=50 cm、CSR分别为1∶4和1∶8时，六个典型监测点的速度时程曲线如图10所示。从图中可知，CSR为1∶8时监测点A1、A2、A3的PVV甚至略高于CSR为1∶4的PPV。但随着爆炸应力波传播到充填体内，CSR为1∶4时，B1、B2、B3三个监测点振动响应更快，到达PPV所需的时间也更短，且PPV值均比CSR为1∶8时更大。表明在相同条件下，当CSR为1∶4时，尽管达到损伤时需要的Vmax更大，但应力波传播速度越快，波能衰减越慢，损伤长度L因此越大。
![]()
图 10 不同灰砂比下典型监测点的速度时程曲线Figure 10. Velocity time history curve of typical monitoring points at different the CSR3.4 孔边距对不同锯齿宽度胶结充填体损伤的影响
为了探究孔边距SHD对胶结充填体的影响，选取SW=0、50 cm，CSR=1:8，σh=0.48 MPa，SHD =1.2 m的充填体，分别讨论SHD =1、1.2、1.5 m情况下，胶结充填体在爆破动载影响下的损伤情况，相对应的数值模型位置为图2a中的模拟区域3，工况方案见表5。
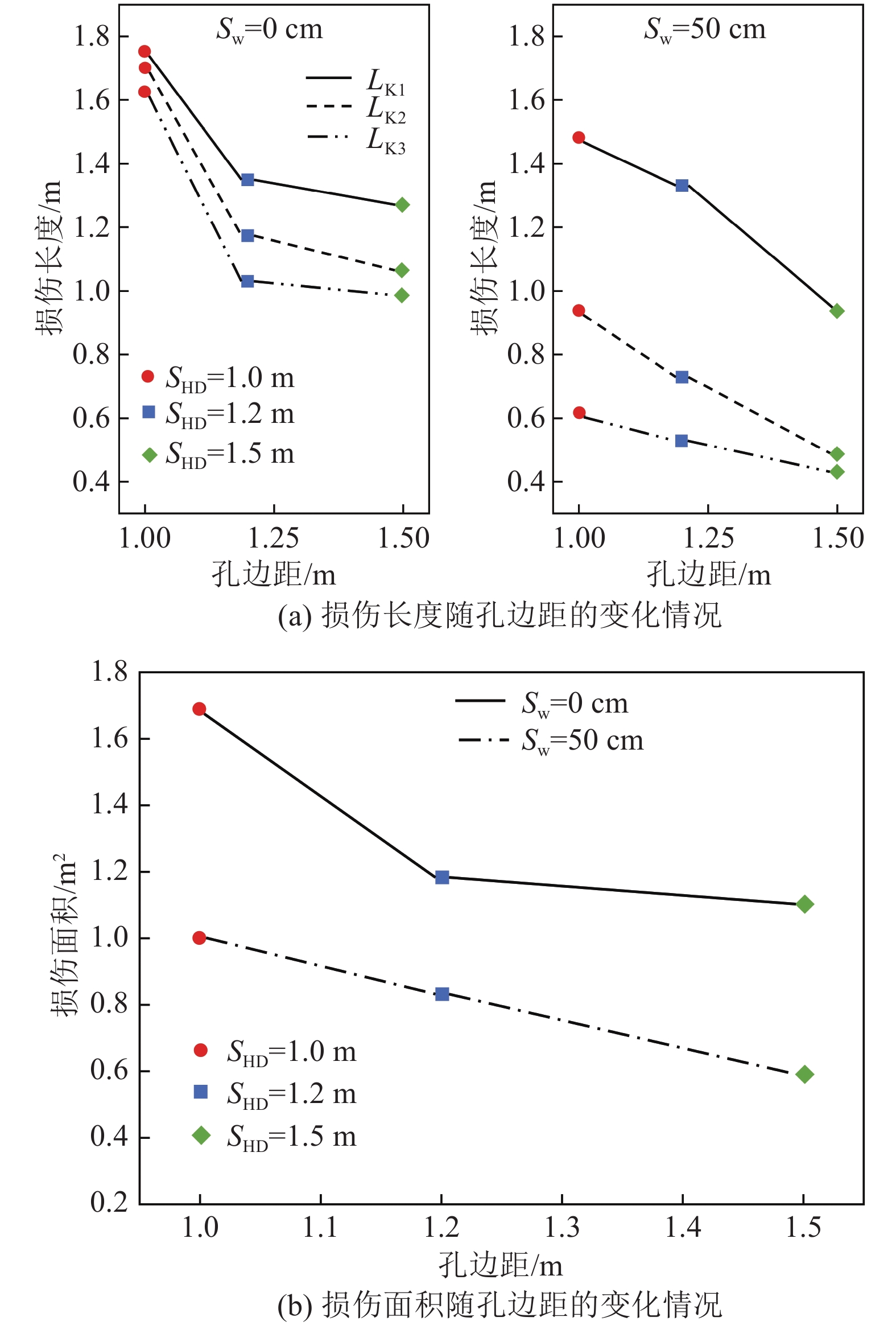
表 5 模拟孔边距变化的工况方案Table 5. Working condition that simulate variations in the SHD工况编号 模拟区域 CSR SW/cm SHD/m σh/MPa 工况1 区域3 1:8 0 1 0.48 工况2 区域3 1:8 0 1.2 0.48 工况3 区域3 1:8 0 1.5 0.48 工况4 区域3 1:8 50 1 0.48 工况5 区域3 1:8 50 1.2 0.48 工况6 区域3 1:8 50 1.5 0.48 同样地，根据数值模拟计算结果所得到的胶结充填体模型K1、K2、K3三列监测线上的PPV，经过数据分析，提取出每列监测线上超过Vmax(17.1 cm/s)且距岩−充界面最远处的坐标，最终得到SW=0、50 cm情况下，不同SHD时胶结充填体模型中各列监测线的L，如图11a所示，根据数值模型计算结果和各监测线上的L，得出了不同SHD下，SW=0、50 cm时的S，如图11b所示。
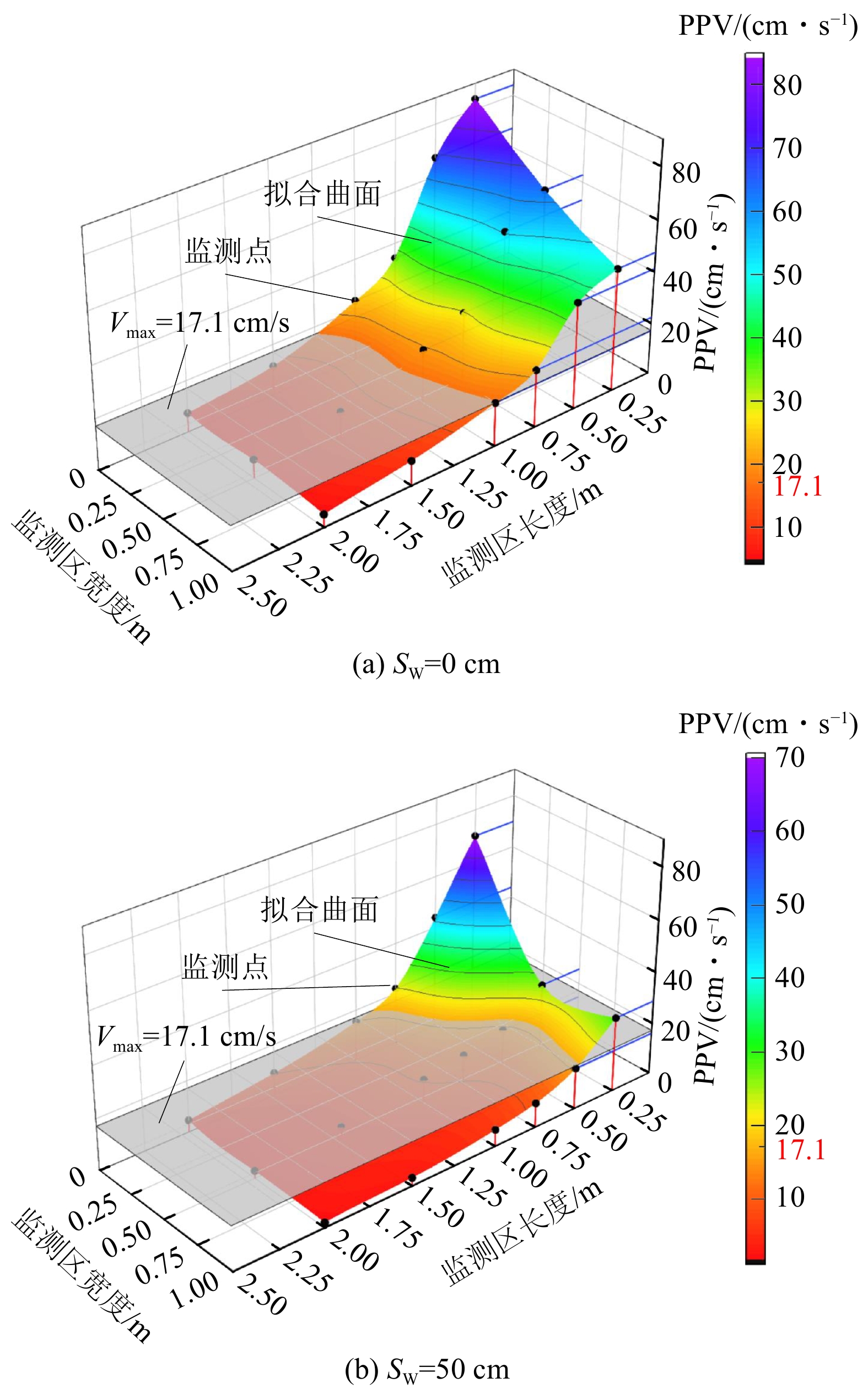
由图11a可知，相同SW下，随着SHD的增大，胶结充填体相同监测线方向上的L逐渐减小，如SW=50 cm，SHD =1 m时，K2方向上的最大损伤长度L2=0.94 m；SHD =1.2 m时，L2=0.73 m；SHD =1.5 m时，L2=0.48 m；此外，当SHD相同时，锯齿状岩−充界面下胶结充填体的L均小于平面状岩−充界面，如当SHD =1.5 m时，平面状岩−充界面(SW=0 cm)时K3方向上的L3=0.99 m，而锯齿状岩−充界面(SW=50 cm)时L3=0.44 m，L折减了55.6%。结合图11b可知，SW相同时，S随着SHD的增大而减小，特别是当岩−充界面为锯齿状时，如SW=50 cm时，SHD与S呈线性负相关；同样地，SHD相同时，S随SW增大而减小。
当SHD =1.5 m时，平面状岩−充界面(SW=0 cm)和锯齿状岩−充界面(SW=50 cm)胶结充填体监测区内的PPV递减趋势如图12所示。可知当SW=0 cm时，胶结充填体内质点振动速度超过Vmax的区域形状近似矩形状，而当SW=50 cm时，胶结充填体内质点振动速度超过Vmax的区域形状近似菱形状，结合图11b可知，SW增大时，虽然S将变小，但损伤区域容易发展为楔形破坏，该结论与3.2.3节结论相符。
3.5 垂直应力对不同锯齿宽度胶结充填体损伤的影响
为了探究垂直应力σh对组合胶结充填体的影响，选取CSR为1:8，SW=0、50 cm， SHD =1.2 m的数值模型，分别讨论σh=0.15 MPa(模拟区域2)、0.48 MPa(模拟区域3)、0.66 MPa(模拟区域4)工况下，组合胶结充填体在爆破动载下的损伤情况，工况方案见表6。
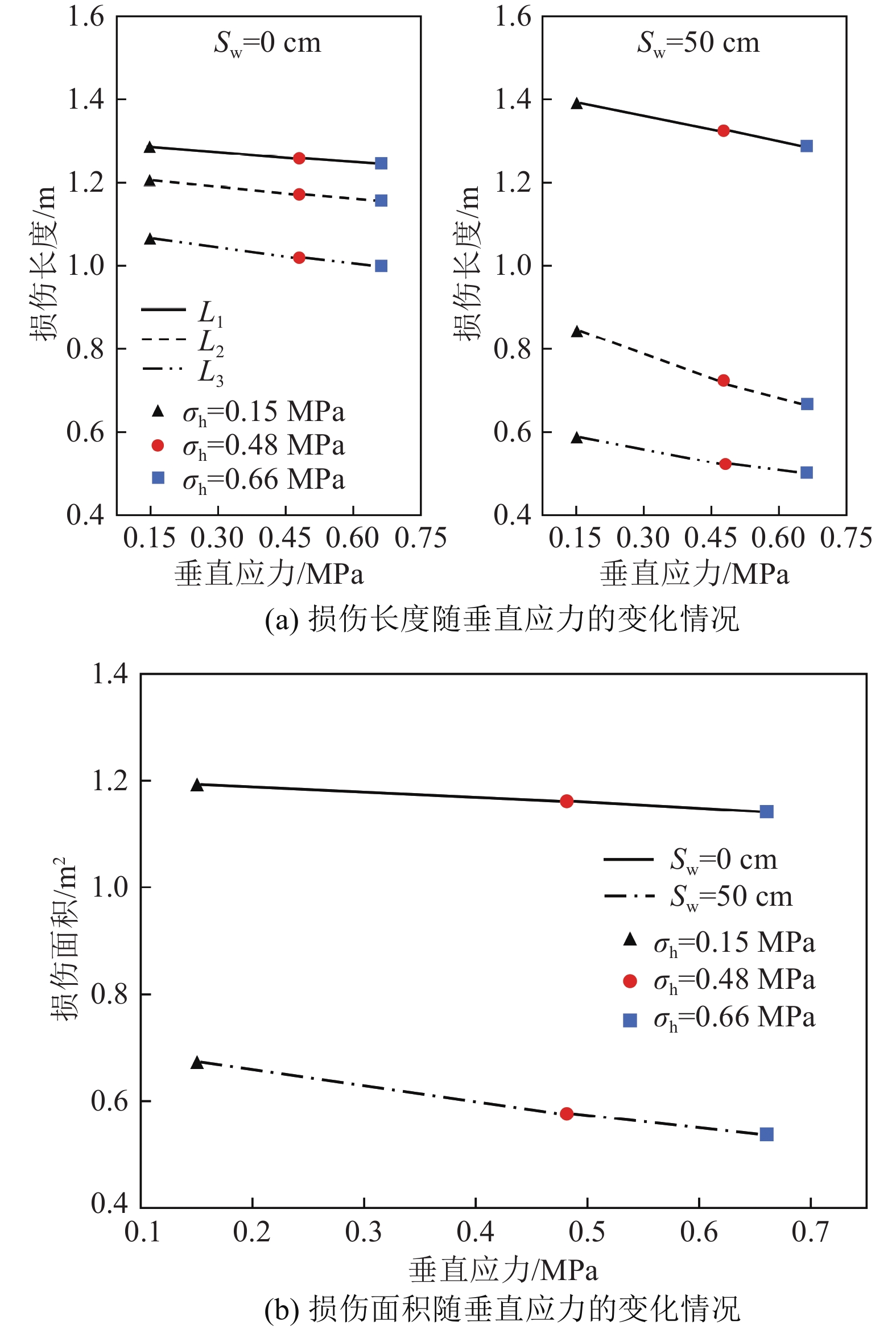
表 6 模拟垂直应力变化的工况方案表Table 6. Working condition that simulate variations in the σh工况编号 模拟区域 CSR SW/cm SHD/m σh/MPa 工况1 区域2 1∶8 0 1.2 0.15 工况2 区域3 1∶8 0 1.2 0.48 工况3 区域4 1∶8 0 1.2 0.66 工况4 区域2 1∶8 50 1.2 0.15 工况5 区域3 1∶8 50 1.2 0.48 工况6 区域4 1∶8 50 1.2 0.66 根据数值模拟计算结果所得到的K1、K2、K3三列监测线上的PPV，经过数据分析，提取出每列监测线上超过Vmax(17.1 cm/s)且距岩−充界面最远处的坐标，最终得到SW=0、50 cm工况下，不同σh对各列监测线上L的影响，如图13a所示，同样地，计算出不同σh下，SW=0、50 cm时的S，如图13b所示。
从图13a可以看出，当SW=0、50 cm时，各监测线方向上的L依旧服从L1 > L2 > L3的规律。相同SW下，随着σh的增大，胶结充填体相同监测线方向上的L逐渐减小，如SW=50 cm，σh=0.15 MPa时，K2方向上的最大损伤长度L2=0.85 m；σh=0.48 MPa时，L2=0.73 m；σh=0.66 MPa时，L2=0.67 m。此外，当SW增大时，K1监测线上的L均增大，K2、K3监测线方向上的损L均减小，这符合3.2.3节中SW的增大将使得胶结充填体的损伤区域形状由近似矩形状向近似菱形过渡的结论。
由图13b可知，对于相同SW，随着σh增大，胶结充填体的整体损伤区域越小，原因在于同一个采场内，胶结充填体受到的水平应力相近，而相同CSR的充填体，当σh较大时，充填体颗粒的位移被抑制得更为严重，因此充填体的振动速度减小，爆炸应力波将被抑制传播；相反，当σh较小时爆炸应力波被促进传播[44-45]。此外，在相同σh下，SW=0 cm时S更大。
4. 结 论
1)平面状岩−充界面下胶结充填体的损伤区域形状近似于矩形，当锯齿宽度增大时，锯齿状岩−充界面下的损伤区域形状接近似于菱形，且锯齿宽度越大，胶结充填体更易发生楔形破坏。因此，在研究胶结充填体因近场爆破而发生损伤破坏时，岩−充界面不宜简单假设为平面状。
2)对于不同灰砂比的组合胶结充填体，当垂直应力相近时，高灰砂比充填层的峰值振动速度更大，爆炸应力波波能衰减越慢，爆破动载更容易在灰砂比不同的两层充填体间诱发错动，高灰砂比充填层的损伤面积略大于低灰砂比充填层。
3)在同一个采场内，同一灰砂比下胶结充填体承受的垂直应力越大，损伤面积越小；胶结充填体的损伤面积随着孔边距的增大而减小，模拟结果表明，当孔边距大于1.5 m时，胶结充填体的损伤区域将能被有效控制在可接受的范围内。
-
![]()
图 5 不同锯齿宽度下胶结充填体的振动速度变化情况
Figure 5. Variation of vibration velocity of backfill at the different SW
![]()
图 6 不同锯齿宽度时各监测点速度时程曲线
Figure 6. Velocity time history curve of each monitoring point under the different SW
![]()
图 10 不同灰砂比下典型监测点的速度时程曲线
Figure 10. Velocity time history curve of typical monitoring points at different the CSR
表 1 矿体、岩体物理力学参数
Table 1 Mechanical properties of orebody and rock
名称 密度
ρ/(kg·m−3)泊松比
μm内摩擦角
Φm/(°)黏聚力
cm/MPa弹性模量
Em/GPa抗压强度
σc/MPa抗拉强度
σmt/MPa围岩 2700 0.30 41.45 3.64 34.64 74.7 3.22 矿体 2810 0.25 37.92 1.98 38.25 65.3 4.87 
下载: 导出CSV
表 2 胶结充填体物理力学参数
Table 2 Mechanical properties of backfill
灰砂比 密度
ρ/(kg·m−3)泊松比
μ内摩擦角
Φ/(°)粘聚力
c/MPa弹性模量
E/MPa抗压强度
σc/MPa抗拉强度
σt/MPa动态抗拉强度
σtd/MPa1:4 1712 0.28 32.4 1.39 274 1.64 0.32 0.41 1:8 1730 0.29 29.8 0.40 116 1.26 0.12 0.18
下载: 导出CSV
表 3 模拟锯齿宽度变化的工况方案
Table 3 Working condition that simulate variations in the SW
工况编号 模拟区域 CSR SW/cm SHD/m σh/MPa 工况1 区域2 1∶8 0 1.2 0.15 工况2 区域2 1∶8 30 1.2 0.15 工况3 区域2 1∶8 40 1.2 0.15 工况4 区域2 1∶8 50 1.2 0.15
下载: 导出CSV
表 4 模拟灰砂比变化的工况方案
Table 4 Working condition that simulate variations in the CSR
工况编号 模拟区域 CSR SW/cm SHD/m σh/MPa 工况1 区域1 1∶4 0 1.2 0.12 工况2 区域2 1∶8 0 1.2 0.15 工况3 区域1 1∶4 50 1.2 0.12 工况4 区域2 1∶8 50 1.2 0.15
下载: 导出CSV
表 5 模拟孔边距变化的工况方案
Table 5 Working condition that simulate variations in the SHD
工况编号 模拟区域 CSR SW/cm SHD/m σh/MPa 工况1 区域3 1:8 0 1 0.48 工况2 区域3 1:8 0 1.2 0.48 工况3 区域3 1:8 0 1.5 0.48 工况4 区域3 1:8 50 1 0.48 工况5 区域3 1:8 50 1.2 0.48 工况6 区域3 1:8 50 1.5 0.48
下载: 导出CSV
表 6 模拟垂直应力变化的工况方案表
Table 6 Working condition that simulate variations in the σh
工况编号 模拟区域 CSR SW/cm SHD/m σh/MPa 工况1 区域2 1∶8 0 1.2 0.15 工况2 区域3 1∶8 0 1.2 0.48 工况3 区域4 1∶8 0 1.2 0.66 工况4 区域2 1∶8 50 1.2 0.15 工况5 区域3 1∶8 50 1.2 0.48 工况6 区域4 1∶8 50 1.2 0.66
下载: 导出CSV
-
[1] 何满潮,谢和平,彭苏萍,等. 深部开采岩体力学研究[J]. 岩石力学与工程学报,2005,24(16):2803−2813. doi: 10.3321/j.issn:1000-6915.2005.16.001 HE Manchao, XIE Heping, PENG Suping, et al. Study on rock mechanics in deep mining engineering[J]. Chinese Journal of Rock Mechanics and Engineering,2005,24(16):2803−2813. doi: 10.3321/j.issn:1000-6915.2005.16.001
[2] 谢和平,高峰,鞠杨. 深部岩体力学研究与探索[J]. 岩石力学与工程学报,2015,34(11):2161−2178. XIE Heping, GAO Feng, JU Yang. Research and development of rock mechanics in deep ground engineering[J]. Chinese Journal of Rock Mechanics and Engineering,2015,34(11):2161−2178.
[3] 张海波,宋卫东. 评述国内外充填采矿技术发展现状[J]. 中国矿业,2009,18(12):59−62. doi: 10.3969/j.issn.1004-4051.2009.12.018 ZHANG Haibo, SONG Weidong. Discussion on the current state of backfill mining from the domestic and foreign development[J]. China Mining Magazine,2009,18(12):59−62. doi: 10.3969/j.issn.1004-4051.2009.12.018
[4] XUE G L, YILMAZ E, WANG Y D. Progress and prospects of mining with backfill in metal mines in China[J]. International Journal of Minerals, Metallurgy and Materials,2023,30(8):1455−1473. doi: 10.1007/s12613-023-2663-0
[5] HUO X F, SHI X Z, QIU X Y, et al. Rock damage control for large-diameter-hole lateral blasting excavation based on charge structure optimization[J]. Tunnelling and Underground Space Technology,2020,106:103569. doi: 10.1016/j.tust.2020.103569
[6] 颜峰,姜福兴. 爆炸冲击载荷作用下岩石的损伤实验[J]. 爆炸与冲击,2009,29(3):275−280. doi: 10.3321/j.issn:1001-1455.2009.03.009 YAN Feng, JIANG Fuxing. Experiment on rock damage under blasting load[J]. Explosion and Shock Waves,2009,29(3):275−280. doi: 10.3321/j.issn:1001-1455.2009.03.009
[7] 费鸿禄,杨卫风,张国辉,等. 金属矿山矿柱回采时爆破荷载下采空区的围岩稳定性[J]. 爆炸与冲击,2013,33(4):344−350. doi: 10.3969/j.issn.1001-1455.2013.04.002 FEI Honglu, YANG Weifeng, ZHANG Guohui, et al. Surrounding rock stability of mined-out area under blast loading in metal mine pillar robbing[J]. Explosion and Shock Waves,2013,33(4):344−350. doi: 10.3969/j.issn.1001-1455.2013.04.002
[8] 杨小林,王树仁. 岩石爆破损伤断裂的细观机理[J]. 爆炸与冲击,2000,20(3):247−252. doi: 10.3321/j.issn:1001-1455.2000.03.009 YANG Xiaolin, WANG Shuren. Meso-mechanism of damage and fracture on rock blasting[J]. Explosion and Shock Waves,2000,20(3):247−252. doi: 10.3321/j.issn:1001-1455.2000.03.009
[9] TAN Y Y, YU X, ELMO D, et al. Experimental study on dynamic mechanical property of cemented tailings backfill under SHPB impact loading[J]. International Journal of Minerals, Metallurgy, and Materials,2019,26(4):404−416. doi: 10.1007/s12613-019-1749-1
[10] LIU B, GAO Y T, JIN A B, et al. Dynamic characteristics of superfine tailings–blast furnace slag backfill featuring filling surface[J]. Construction and Building Materials,2020,242:118173. doi: 10.1016/j.conbuildmat.2020.118173
[11] CAO S, YILMAZ E, SONG W D. Dynamic response of cement-tailings matrix composites under SHPB compression load[J]. Construction and Building Materials,2018,186:892−903. doi: 10.1016/j.conbuildmat.2018.08.009
[12] 谭玉叶,汪杰,宋卫东,等. 循环冲击下胶结充填体动载力学特性试验研究[J]. 采矿与安全工程学报,2019,36(1):184−190,197. TAN Yuye, WANG Jie, SONG Weidong, et al. Experimental study on mechanical properties of cemented tailings backfill under cycle dynamic loading test[J]. Journal of Mining & Safety Engineering,2019,36(1):184−190,197.
[13] 姜立春,苏勇,代庆松. 远场爆破水平应力波扰动下分层胶结充填体矿柱的动力响应机制[J]. 岩石力学与工程学报,2020,39(1):34−44. JIANG Lichun, SU Yong, DAI Qingsong. Dynamic response mechanisms of layered cemented backfill pillars under horizontal stress wave disturbance of far-field blasting[J]. Chinese Journal of Rock Mechanics and Engineering,2020,39(1):34−44.
[14] 黄欣成,卢文波,张立新,等. 全尾砂胶结充填体的爆破振动破坏机制和振动速度阈值研究[J]. 爆破,2021,38(1):1−7. doi: 10.3963/j.issn.1001-487X.2021.01.001 HUANG Xincheng, LU Wenbo, ZHANG Lixin, et al. Study on blasting vibration failure mechanism and vibration velocity threshold of total tailing cemented backfill[J]. Blasting,2021,38(1):1−7. doi: 10.3963/j.issn.1001-487X.2021.01.001
[15] 朱鹏瑞,宋卫东,曹帅,等. 爆破动载下胶结充填体的张拉力学响应机制[J]. 采矿与安全工程学报,2018,35(3):605−611. ZHU Pengrui, SONG Weidong, CAO Shuai, et al. Tensile mechanical response mechanism of cemented backfills under blasting load[J]. Journal of Mining & Safety Engineering,2018,35(3):605−611.
[16] SUAZO G, VILLAVICENCIO G. Numerical simulation of the blast response of cemented paste backfilled stopes[J]. Computers and Geotechnics,2018,100:1−14. doi: 10.1016/j.compgeo.2018.04.007
[17] EMAD M Z, MITRI H, KELLY C. Dynamic model validation using blast vibration monitoring in mine backfill[J]. International Journal of Rock Mechanics and Mining Sciences,2018,107:48−54. doi: 10.1016/j.ijrmms.2018.04.047
[18] EMAD M Z, MITRI H, KELLY C. Effect of blast-induced vibrations on fill failure in vertical block mining with delayed backfill[J]. Canadian Geotechnical Journal,2014,51(9):975−983. doi: 10.1139/cgj-2013-0305
[19] LI G W, DENG G Z, MA J G. Numerical modelling of the response of cemented paste backfill under the blasting of an adjacent ore stope[J]. Construction and Building Materials,2022,343:128051. doi: 10.1016/j.conbuildmat.2022.128051
[20] 胡建华,张涛,丁啸天,等. 充−岩界面耦合体爆破动力响应机理[J]. 爆炸与冲击,2021,41(8):164−178. HU Jianhua, ZHANG Tao, DING Xiaotian, et al. Dynamic response mechanism of a rock-filling interfacial coupling body to blasting in it[J]. Explosion and Shock Waves,2021,41(8):164−178.
[21] 刘立波,李建春,李海波,等. 应力波斜入射黏弹性节理的传播规律[J]. 岩石力学与工程学报,2012,31(S2):3593−3598. LIU Libo, LI Jianchun, LI Haibo, et al. Propagation law of oblique incidence of stress wave across a viscoelastic joint[J]. Chinese Journal of Rock Mechanics and Engineering,2012,31(S2):3593−3598.
[22] 刘啸,华心祝,黄志国,等. 应力波作用下含大型结构面岩体垮塌动力失稳机制[J]. 岩石力学与工程学报,2021,40(10):2003−2014. LIU Xiao, HUA Xinzhu, HUANG Zhiguo, et al. Dynamic collapse mechanisms of rock mass with large structural planes under stress waves[J]. Chinese Journal of Rock Mechanics and Engineering,2021,40(10):2003−2014.
[23] SHARPE J A. The production of elastic waves by explosion pressures. I. Theory and empirical field observations[J]. Geophysics,1942,7(2):144. doi: 10.1190/1.1445002
[24] SAINOKI A, MITRI H S. Numerical simulation of rock mass vibrations induced by nearby production blast[J]. Canadian Geotechnical Journal,2014,51(11):1253−1262. doi: 10.1139/cgj-2013-0480
[25] SITHARAM T G. Geotechnical applications for earthquake engineering:Research Advancements[M]. Hershey:IGI Global, 2012:160−170.
[26] VAN Goolbronwyn. Effects of blasting on the stability of paste fill stopes at Cannington Mine[D]. Townsville:James Cook University, 2007:102−108.
[27] CHEN S H, WU J, ZHANG Z H. Blasting source equivalent load on elastic–plastic boundary for rock blasting[J]. Journal of Engineering Mechanics,2017,143(7):1−7.
[28] EMAD Muhammad Zaka, Dynamic Performance of Cemented Rockfill under Blast-Induced Vibrations[D]. Montreal:University of McGill, 2014:73−77.
[29] 冷振东,卢文波,陈明,等. 岩石钻孔爆破粉碎区计算模型的改进[J]. 爆炸与冲击,2015,35(1):101−107. doi: 10.11883/1001-1455(2015)01-0101-07 LENG Zhendong, LU Wenbo, CHEN Ming, et al. Improved calculation model for the size of crushed zone around blasthole[J]. Explosion and Shock Waves,2015,35(1):101−107. doi: 10.11883/1001-1455(2015)01-0101-07
[30] 李芳涛,胡志平,陈南南,等. 爆破荷载作用下隧道围岩裂隙范围计算方法研究[J]. 振动与冲击,2022,41(8):260−269. LI Fangtao, HU Zhiping, CHEN Nannan, et al. A study of fracture range of tunnel surrounding rock under blasting[J]. Journal of Vibration and Shock,2022,41(8):260−269.
[31] 杨建华,吴泽南,姚池,等. 地应力对岩石爆破开裂及爆炸地震波的影响研究[J]. 振动与冲击,2020,39(13):64−70,90. YANG Jianhua, WU Zenan, YAO Chi, et al. Influences of in situ stress on blast-induced rock fracture and seismic waves[J]. Journal of Vibration and Shock,2020,39(13):64−70,90.
[32] 叶志伟,陈明,李桐,等. 小不耦合系数装药爆破孔壁压力峰值计算方法[J]. 爆炸与冲击,2021,41(6):116−126. YE Zhiwei, CHEN Ming, LI Tong, et al. A calculation method of the peak pressure on borehole wall for low decoupling coefficient charge blasting[J]. Explosion and Shock Waves,2021,41(6):116−126.
[33] LU W B, YANG J H, CHEN M, et al. An equivalent method for blasting vibration simulation[J]. Simulation Modelling Practice and Theory,2011,19(9):2050−2062. doi: 10.1016/j.simpat.2011.05.012
[34] YI C P, JOHANSSON D, GREBERG J. Effects of in situ stresses on the fracturing of rock by blasting[J]. Computers and Geotechnics,2018,104:321−330. doi: 10.1016/j.compgeo.2017.12.004
[35] BLAIR D P. A comparison of Heelan and exact solutions for seismic radiation from a short cylindrical charge[J]. Geophysics,2007,72(2):E33−E41. doi: 10.1190/1.2424543
[36] YI C P, JOHANSSON D, NYBERG U, et al. Stress wave interaction between two adjacent blast holes[J]. Rock Mechanics and Rock Engineering,2016,49(5):1803−1812. doi: 10.1007/s00603-015-0876-x
[37] 雷刚,李元辉,徐世达,等. 基于FLAC3D模拟的深部岩体爆破损伤规律研究[J]. 金属矿山,2017(10):135−140. doi: 10.3969/j.issn.1001-1250.2017.10.027 LEI Gang, LI Yuanhui, XU Shida, et al. Simulation study on blasting damage law of deep rock mass based on FLAC3D[J]. Metal Mine,2017(10):135−140. doi: 10.3969/j.issn.1001-1250.2017.10.027
[38] 甘肃,郑怀昌,赵忠琦,等. 远爆区爆破对胶结充填体损伤特性研究[J]. 矿业研究与开发,2019,39(7):78−83. GAN Su, ZHENG Huaichang, ZHAO Zhongqi, et al. Study on the damage properties of cemented filling body by blasting in the remote blasting area[J]. Mining Research and Development,2019,39(7):78−83.
[39] 王振昌. 二步回采围岩和充填体爆破损伤特征及安全阈值研究[D]. 福州:福州大学,2018 :105−107. WANG Zhenchang. Study on blasting damage characteristics and safety threshold of surrounding rock and backfill in two-step mining [D]. Fuzhou:Fuzhou University, 2018 :105−107.
[40] 杨伟,李国平,李夕兵,等. 爆破荷载下全尾砂胶结充填体破坏规律及防治措施[J]. 矿业研究与开发,2018,38(3):113−118. YANG Wei, LI Guoping, LI Xibing, et al. The failure rules and preventive measures of cemented full tailings filling body under blasting load[J]. Mining Research and Development,2018,38(3):113−118.
[41] 刘西森. 层状岩体隧道爆破开挖引起的非对称振动传播规律研究[D]. 焦作:河南理工大学,2022:18−25. LIU Xisen. Propagation law of asymmetric vibration induced by tunnel blasting in layered rock[D]. Jiaozuo:Henan Polytechnic University, 2022:18−25.
[42] 杨仁树,李炜煜,李永亮,等. 3种岩石动态拉伸力学性能试验与对比分析[J]. 煤炭学报,2020,45(9):3107−3118. YANG Renshu, LI Weiyu, LI Yongliang, et al. Comparative analysis on dynamic tensile mechanical properties of three kinds of rocks[J]. Journal of China Coal Society,2020,45(9):3107−3118.
[43] 李杨,王雁冰,付代睿,等. 动载下层状复合岩石能量耗散及断裂特征研究[J]. 工程科学学报,2023,45(11):1833−1846. LI Yang, WANG Yanbing, FU Dairui, et al. Energy dissipation and fracture characteristics of composite layered rock under dynamic load[J]. Chinese Journal of Engineering,2023,45(11):1833−1846.
[44] 刘鑫,兰涛,秦广冲,等. 地应力对混凝土材料中爆炸应力波传播影响规律研究[J]. 爆破,2023,40(3):151−157,205. doi: 10.3963/j.issn.1001-487X.2023.03.021 LIU Xin, LAN Tao, QIN Guangchong, et al. Study on influence of in situ stress on propagation of explosion stress wave in concrete[J]. Blasting,2023,40(3):151−157,205. doi: 10.3963/j.issn.1001-487X.2023.03.021
[45] 杨建华,孙文彬,姚池,等. 高地应力岩体多孔爆破破岩机制[J]. 爆炸与冲击,2020,40(7):10. YANG Jianhua, SUN Wenbin, YAO Chi, et al. Mechanism of rock fragmentation by multi-hole blasting in highly-stressed rock masses[J]. , Explosion and Shock Waves,2020,40(7):10.
计量
- 文章访问数: 87
- HTML全文浏览量: 11
- PDF下载量: 18
