Electromechanical coupling dynamics behavior of permanent magnet motor semi-direct driving scraper conveyor
-
摘要:
针对刮板输送机传统异步电机驱动系统传动效率低、工作能耗高以及永磁直驱系统径向尺寸大难以适应综采工作面安装空间及过载工况等问题,设计了一种新型永磁电机半直驱系统,利用MATLAB/Simulink仿真软件与台架试验研究了永磁半直驱刮板输送机的机−电耦合动力学行为。首先,基于永磁电机驱动技术,以SGZ1000/2000型刮板输送机为例,设计了一种永磁电机半直驱系统,并完成了驱动系统关键参数设计。其次,推导齿轮传动系统动力学模型,基于状态空间方程建模法搭建永磁电机半直驱刮板输送机的机−电耦合动力学仿真模型,通过仿真试验研究了永磁电机半直驱刮板输送机在多种工况下的机−电耦合动力学行为;结果表明:永磁电机半直驱系统在空载启动定常落煤、非定常落煤以及故障后满载启动3种工况下,能够实现零速重载运行、输出转速与电磁转矩的快速响应以及动态调节;在启动瞬间与负载突变下,链条速度、加速度与张力会发生明显波动,其中:在机头与机尾链轮处的波动峰值最大;随着链条传递波动峰值会发生衰减,距离机头与机尾链轮越远,波动峰值越小。再次,利用永磁电机半直驱系统试验台,开展空载启动落煤与满载启动模拟试验,得到了永磁电机半直驱系统的动态特性,试验结果与机−电耦合动力学模型的仿真结果基本一致。最后,基于台架试验性能参数,通过对比永磁电机半直驱系统与传统异步电机驱动系统的驱动性能后得到:永磁电机半直驱系统在全负载点的驱动效率均优于传统异步电机驱动系统,至少提升了16.3%以上,可显著提高矿山运输装备的节电率,有助于推进矿山朝着绿色低碳方向发展。
Abstract:Aiming at the problems of low transmission efficiency and high energy consumption of the traditional induction motor drive system of the scraper conveyor, and the radial size of the permanent magnet direct driving system which is too large and difficult to be installed in the downhole working face, a new type of semi-direct driving system of permanent magnet motors is designed, and the electromechanical coupling dynamics behavior of the semi-direct drive scraper conveyor of permanent magnet is investigated by using the simulation software of MATLAB/Simulink and the test of the bench. First, a semi-direct driving system based on permanent magnet drive technology was designed using the SGZ1000/2000 type scraper conveyor as an example, and the key parameters of the drive system were designed. Then, the dynamic model of the gear transmission system was derived, and a simulation model of the electromechanical coupling dynamics of the permanent magnet motor semi-direct driving scraper conveyor was built based on the state space equation modelling method. On this basis, the electromechanical coupling dynamics behavior of the permanent magnet motor semi-direct driving scraper conveyor under various working conditions was investigated through simulation experiments. The results show that the semi-direct driving system of the permanent magnet motor could realize no-load and heavy-duty operation, fast response of output speed and electromagnetic torque, and dynamic adjustment under the three working conditions of no-load start of constant coal drop, non-constant coal drop, and full-load start after failure; At the moment of starting and under the sudden change of load, the chain speed, acceleration and tension fluctuate significantly, among which the fluctuation peaks are largest in the sprockets of the head and tail; as the fluctuation peaks of the chain transmission decay, the farther away from the head and tail sprockets, the smaller the fluctuation peaks. The fluctuation peaks are attenuated as the chain passes, and the farther away from the head and tail sprockets, the smaller the fluctuation peaks are. Again, using the permanent magnet motor semi-direct driving system test bench, the simulation test of no-load start-up coal drop and full-load start-up is carried out to obtain the dynamic characteristics of the permanent magnet motor semi-direct driving system, and the test results are basically consistent with the simulation results of the electromechanical coupling dynamics model. Finally, based on the experimental performance parameters obtained from the permanent magnet motor semi-direct driving system test bench, after comparing the output torque, electromagnetic torque and other driving performance of the permanent magnet motor semi-direct drive system and the traditional induction motor drive system, we could see that the driving efficiency of the permanent magnet motor semi-direct driving system is better than that of the traditional induction motor driving system at the full load point, which is at least more than 16.3%, which could significantly improve the power saving rate of mine transportation equipment and help promote the development of mining in the green and low-carbon direction. It can significantly improve the power saving rate of mine haulage equipment and help promote the development of mines in the green and low-carbon direction.
-
0. 引 言
煤炭作为推动我国经济发展与保障能源安全稳定的压舱石[1],在未来很长一段时间内仍将是我国主体能源。2023年3月,国家能源局印发《关于加快推进能源数字化智能化发展的若干意见》指出,要以数字化、智能化技术带动煤炭安全高效生产,加快实现采煤工作面采−支−运智能协同运行。近年来,在国家“双碳”战略目标与矿山智能化建设浪潮的驱动下,我国矿山运输装备正朝着智能、绿色与安全方向转型升级[2]。刮板输送机作为煤矿井下主煤流运输系统的关键装备之一,主要承担综采工作面煤炭运输以及向顺槽装载机转运煤炭的重要任务[3],其运行可靠性与高效性直接影响煤矿的生产效率和经济效益[4]。
目前,刮板输送机多采用三相异步电机作为动力源,不管是早期的液力耦合器(TTT)/可控启动装置(CST)的软启动方式[5-6],还是采用变频器的变频启动方式,均需要在链轮上安装机械减速装置,存在传动效率低、故障率高、维护成本高等技术不足,而三相异步电机也存在着启动特性差、启动电流大、功率因数低等问题[7],导致了刮板输送机整机运行能耗高、传动效率低,难以满足矿山装备绿色低碳化发展需求。永磁同步电机凭借其高功率因数、节能省电的优点以及低速大转矩的输出特性,可以舍去减速装置与低速重载工况的矿山运输装备实现直联驱动,大大提高了驱动效率,由于带式输送机在驱动原理上特有的自我保护特性,目前已在煤矿井下带式输送机上得到广泛应用[8]。张磊等[9]研发了一种集永磁直驱技术与永磁电张紧技术于一体的大运距高可靠智能型全永磁驱动带式输送机系统,通过驱动系统综合控制器可统一控制多套永磁直驱系统与永磁张紧绞车的电机工作,极大程度提高了带式输送机的运行效率;王雷等[10]研发了装机功率50~315 kW的带式输送机矿用隔爆永磁电动滚筒,在国内数十个煤矿得到了广泛应用。
永磁电机的低速大转矩输出特性主要得益于其内部转子上的高性能永磁体材料,而永磁体在高温与过电流等极端工况下存在退磁风险。受煤层地质条件与开采工艺影响,用于综采工作面的采煤机与刮板输送机,在运行过程中经常会遇到冲击载荷与突变负载,相比于带式输送机其运行工况更为恶劣,且没有摩擦驱动式设备的超载“打滑”自我保护特性,对驱动系统的可靠性要求更高。因此,目前采煤机与刮板输送机尚未实现永磁驱动化,多停留在系统结构设计与机−电耦合动力学等基础理论研究阶段,用以探究永磁驱动技术在综采工作面使用的可行性。例如,在采煤机永磁驱动技术领域,张务果[11]提出了一种采煤机永磁驱动截割传动系统,其取消了传统采煤机截割滚筒后连接的行星齿轮减速机构,缩短了采煤机截割传动系统的传动链;姜耸等[12]根据永磁电机、齿轮减速系统和末端截割滚筒的耦合关系,建立了永磁驱动截割传动系统的全局机−电耦合动力学模型,分析了传动轴扭转刚度、齿轮啮合刚度和轴承支撑刚度影响下系统固有频率变化规律,为采煤机截割滚筒永磁驱动技术研究提供了参考。
在刮板输送机永磁驱动技术领域,王洋洋[13]、鞠锦勇[14]等探究了永磁直驱刮板输送机在空载、重载与冲击载荷等工况下刮板链传动系统的机−电耦合动态特性;张强等[15]提出了一种新型多永磁电机串联驱动刮板输送机系统,着重分析了建立非线性机−电耦合动力学模型对于描述链传动系统非线性特征的重要性,以上研究均为永磁驱动技术在刮板输送机上应用提供了理论参考。
刮板输送机若采用永磁直驱方案,会因径向尺寸过大导致在综采工作面内难以布置,对此,笔者[16]提出了一种刮板输送机永磁半直驱电机,通过在传统永磁同步电机箱体内部安装行星齿轮减速装置,可在保证低速大转矩输出特性的同时,进一步减小永磁体与定子绕组结构,实现减小电机体积的目的。在此基础上,本文开展了多工况下的机−电耦合动力学行为研究,研究结果可为刮板输送机永磁驱动技术的研究与应用提供理论参考。
1. 刮板输送机永磁电机半直驱系统设计
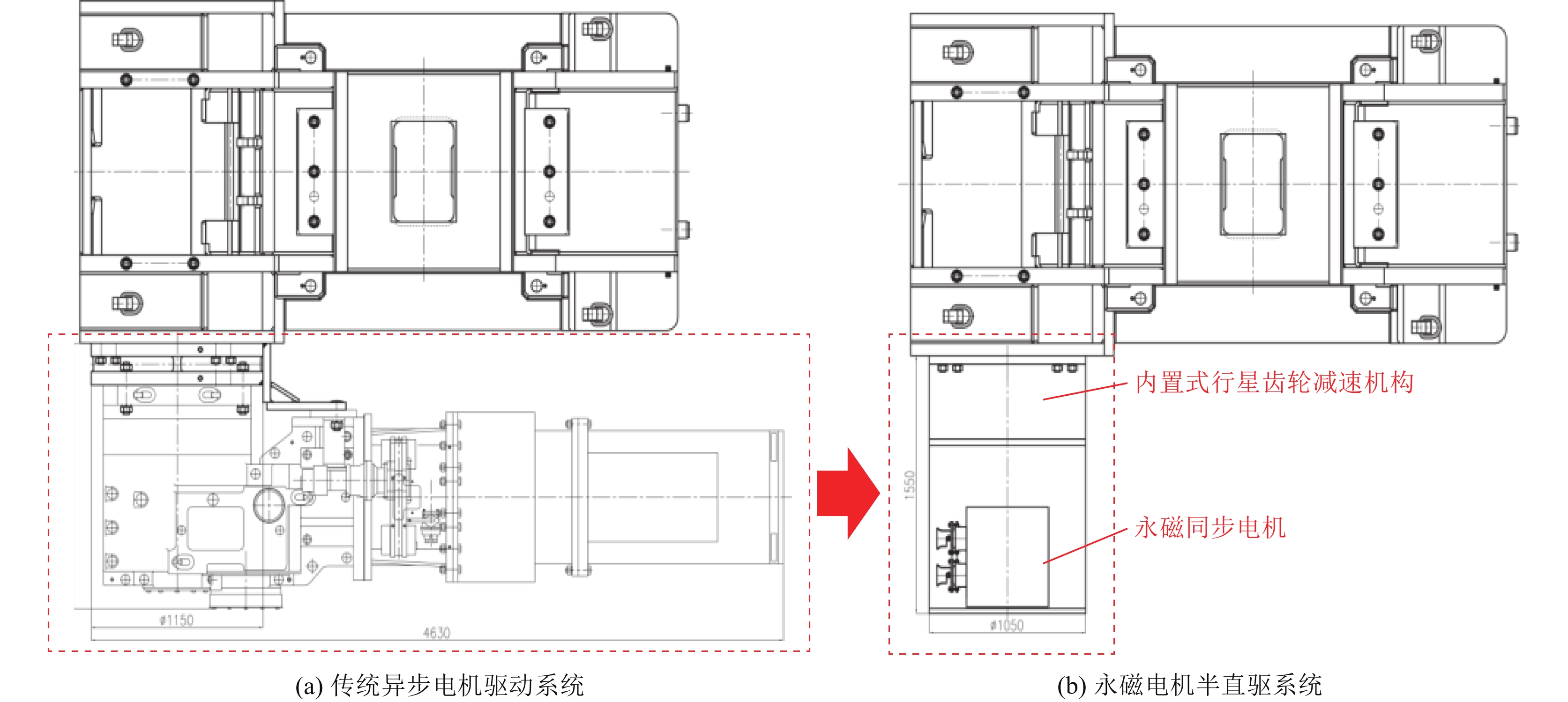
针对刮板输送机传统异步电机驱动性能不足,本文结合永磁同步电机高节电率与大启动转矩的驱动优势,以及行星齿轮减速装置的减速增扭特性,提出并设计了一种新型永磁电机半直驱系统,具体如图1所示。
1.1 永磁电机半直驱系统技术优势分析
分析表明,制约先进永磁直驱技术在刮板输送机上应用的主要原因是综采工作面空间受限及“三机”配套问题。刮板输送机所需驱动功率往往高达数千千瓦,若采用永磁直驱系统,为适应刮板输送机低速重载工况,将会导致电机径向尺寸过于庞大,机身高度过高,无法在矮机身的综采工作面刮板输送机上安装使用。同时,由于煤矿井下煤层地质条件复杂多变,导致采煤机截割落煤过程存在着许多不确定性,由于煤层“片帮”等原因导致刮板输送机瞬间数倍过载的恶劣工况要远多于带式输送机等其他输送装备,而直驱系统缺乏液力耦合器的缓冲保护,在过载工况下容易导致电机堵转产生高温,永磁电机存在退磁导致电机失速的风险。
行星齿轮减速机构相比于传统二级圆柱直齿轮减速器,具有结构紧凑、体积小、重量轻、传动比范围大与承载能力强等众多优势,十分适合于低速重载传动工况使用。因此,基于行星齿轮减速机构以上优点,本研究采用永磁同步电机替换三相异步电机,以内置式行星齿轮减速机构替换传统三相异步电机+减速器的“永磁半直驱”全新技术方案,通过内置式的行星齿轮减速机构,既可以通过行星齿轮减速机构实现减速增扭,还可以削减恶劣运输工况下突变负载对永磁电机的直接冲击,在运行可靠性方面更具优势。
如图2所示,永磁电机半直驱系统采用“永磁同步电机+内置式行星齿轮减速机构”的一体化结构,与传统异步电机驱动系统相比较,其传动链长度缩减了超过70%,重量减少了近50%[5],不仅可有效降低刮板输送机驱动系统的重量,解决刮板输送机的偏心问题,而且也更便于在井下安装和维护。
因此,结合煤矿井下工作面刮板输送机实际运输工况与严苛工作条件分析,采用永磁电机半直驱技术将是刮板输送机提高驱动效率的有效途径。
1.2 永磁电机半直驱系统主要参数设计
本研究选取了较为典型的SGZ1000/2000型刮板输送机传统异步电机驱动系统为研究对象,其原驱动系统由“三相异步电机+液力耦合器+减速器”组成,存在着传动链长、驱动效率低、故障率高以及液力耦合器软启动效果差等技术问题。对此,本研究拟将其升级为永磁电机半直驱系统,表1为该型号刮板输送机主要参数。
表 1 SGZ1000/2000型刮板输送机主要参数Table 1. Main parameters of SGZ1000/2000 scraper conveyor参数 数值 运输距离/m 300 运量能力/(t·h−1) 2500 驱动系统形式 异步电机+液力耦合器+减速器 驱动电机功率/kW 2× 1000 链条型式 中双链 链规格/mm ø48×152 如图3所示,刮板输送机驱动系统机械部分升级改造仅需将原有“三相异步电机+液力耦合器+减速器”从减速器轴端联轴器上拆下,直接更换为永磁电机半直驱系统即可。
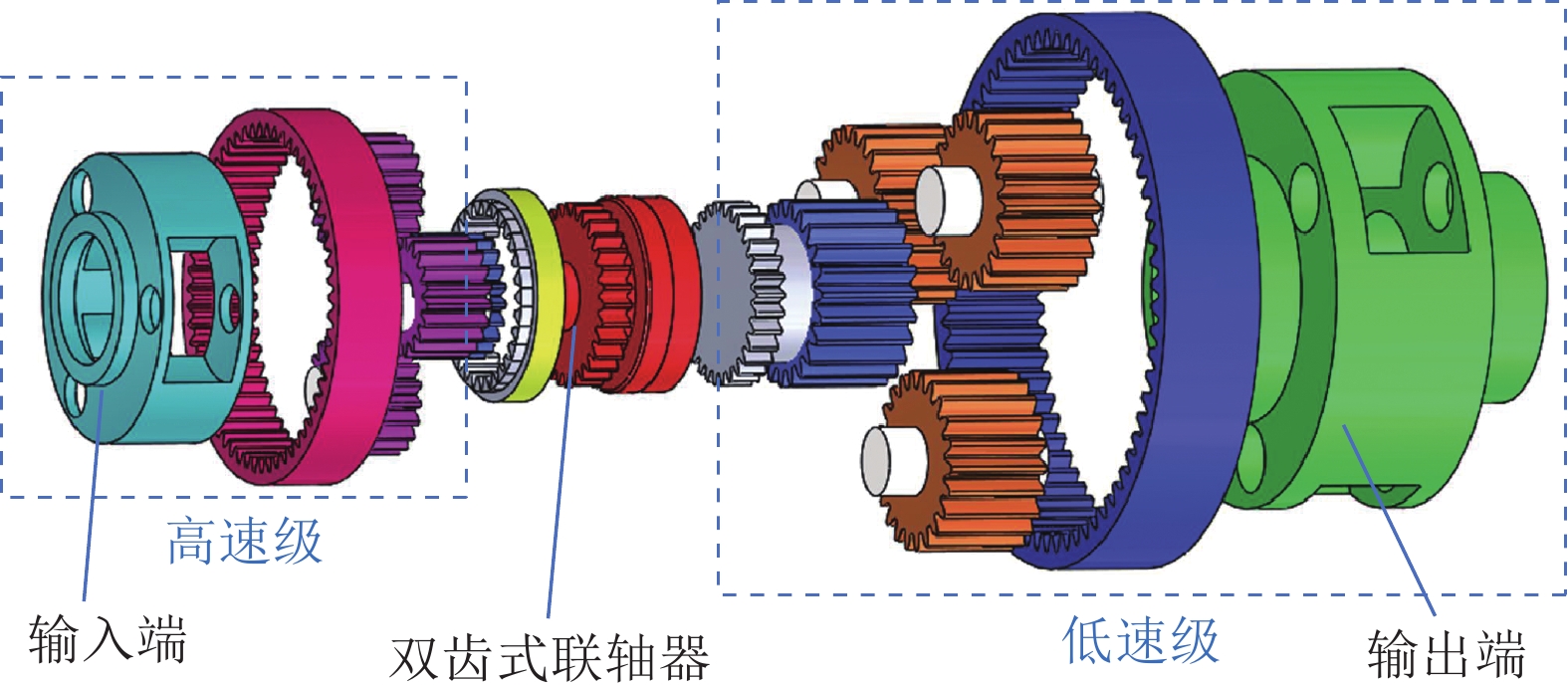
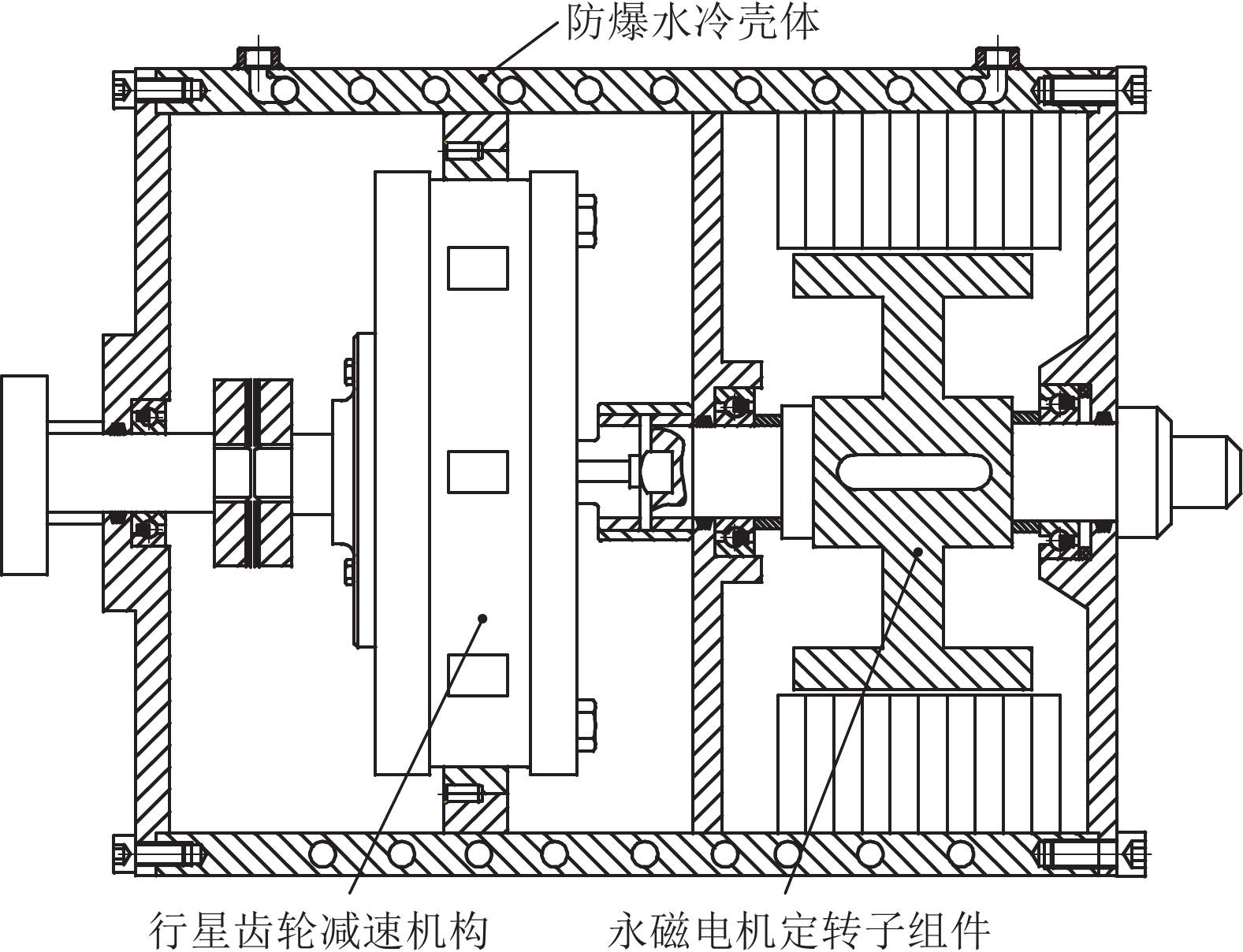
新型永磁电机半直驱系统在永磁同步电机的壳体内加装有行星齿轮减速机构,如图4所示,内置的行星齿轮减速机构采用NGW型行星轮系,输入端通过渐开线花键与永磁同步电机转子轴连接,输出端通过联轴器与刮板输送机链轮连接。采用两级行星齿轮减速机构,高速级与低速级之间通过双齿式联轴器连接,通过传统机械设计方法即可得到表2所示的永磁电机半直驱系统关键参数[17]。
表 2 刮板输送机永磁电机半直驱系统关键参数Table 2. Key parameters of permanent magnet motor semi-direct driving system for scraper conveyor参数 数值 驱动系统形式 变频器+永磁半直驱电机 装机功率/kW 2× 1000 额定电流/A 185 额定电压/V 3300 额定转速/(r·min−1) 750 额定频率/Hz 50 减速机构传动比 15 压力角/(°) 20 模数 10 太阳轮齿数 20、23 行星轮齿数 19、22 2. 永磁电机半直驱刮板输送机的机−电耦合动力学建模
传统刮板输送机静态设计方法,不考虑负载突变对刮板输送机动态特性的影响,将刮板链视作刚体,然而由于刮板链具有明显的粘弹性,其在运行过程中属于多输入非线性时变模型。因此,传统的静态设计方法已经无法满足设计需求。
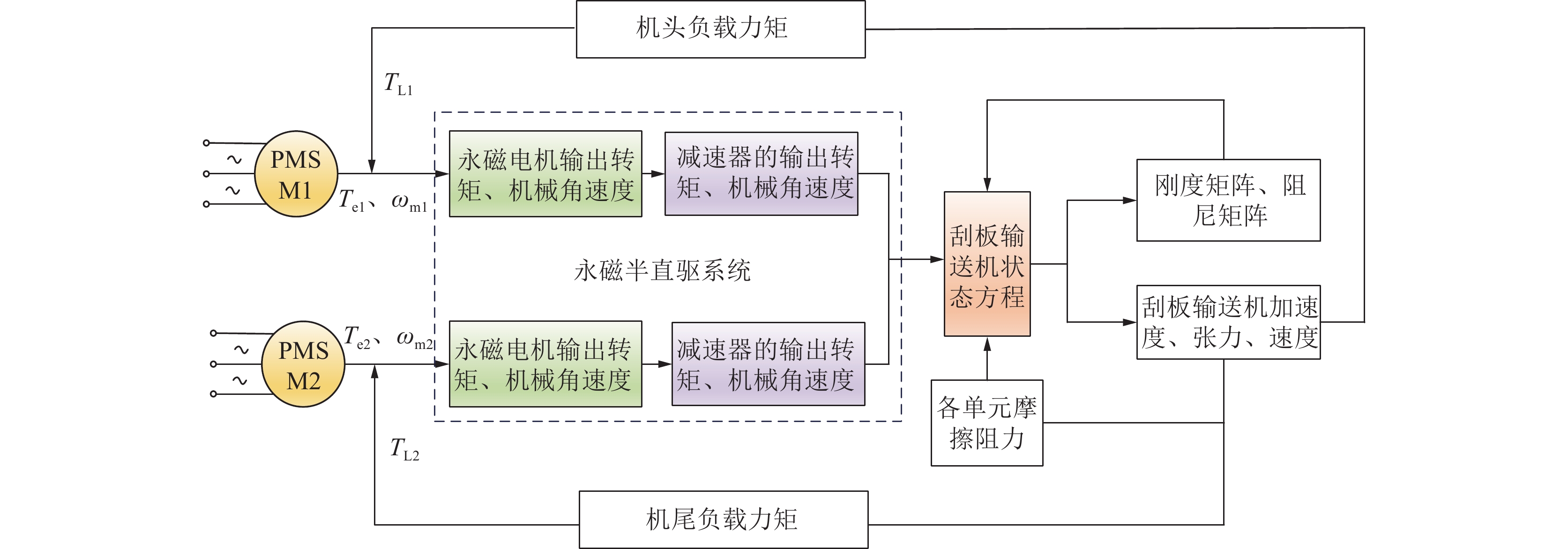
对此,为探究新型永磁电机半直驱系统与刮板输送机机械本体之间的机−电耦合动力学行为,本研究基于状态空间方程建模法,搭建了永磁电机半直驱刮板输送机的机−电耦合动力学模型(图5,图中,Te1、Te2分别为永磁电机1与永磁电机2的输出电磁转矩;TL1、TL2分别为机头负载转矩与机尾负载转矩;ωm1、ωm2为永磁电机1与永磁电机2的机械角速度),包括:行星齿轮减速机构动力学模型、永磁电机矢量控制模型和刮板输送机机械负载动力学模型等。
2.1 永磁半直驱电机齿轮传动系统动力学模型
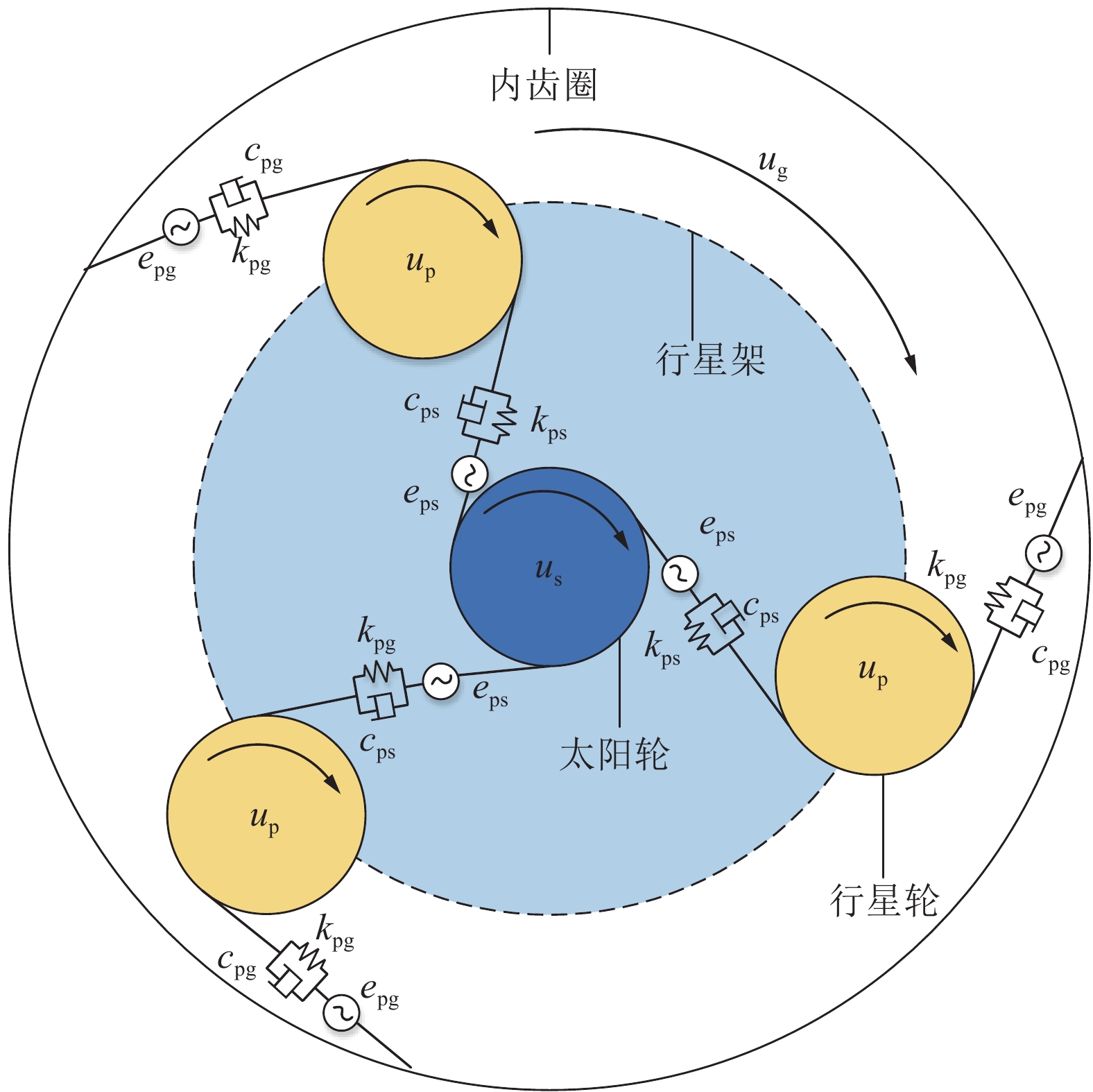
基于图4所设计的行星齿轮减速机构,因行星齿轮减速机构高速级与低速级动力学模型类似,为简化叙述过程,以高速级行星齿轮减速机构进行叙述,建立了如图6所示的半直驱齿轮传动系统动力学模型。规定顺时针方向为正,各齿轮的扭转位移为ui(i=s,p,g),其中:下标s代表太阳轮,下标p代表行星轮、下标g代表内齿圈。kps行星轮与太阳轮之间的啮合刚度、kpg行星轮与内齿圈之间的啮合刚度、cps行星轮与太阳轮之间的阻尼、cpg行星轮与太阳轮之间的阻尼、eps行星轮与太阳轮之间的传动误差、epg行星轮与太阳轮之间的传动误差。
基于图6所示模型,可得到永磁电机半直驱系统内部齿轮传动系统动力学模型,如式(1)所示。
式中:Is为太阳轮的转动惯量;Ip为行星轮转动惯量;Ig为内齿圈的转动惯量;Tin为减速器的输入转矩;$\dot u $(i=s,p,g)、$\ddot u $(i=s,p,g)为各齿轮的扭转速度与加速度;xsp、xpg分别为太阳轮与行星轮、行星轮与内齿圈之间的扭转位移变化量;rs、rp、rg分别为太阳轮、行星轮与内齿圈的啮合半径;αsp为太阳轮与行星轮的啮合角、αpg为内齿圈与行星轮的啮合角。
$$ \left\{ \begin{array}{l} {I_{\rm{s}}}/r_{{\rm{s}}}^2{{\ddot u}_{\rm{s}}} + 3{c_{{\rm{sp}}}}{{\dot x}_{{\rm{sp}}}} + 3{k_{{\rm{sp}}}}{x_{{\rm{sp}}}} = {T_{{\rm{in}}}}/{r_{\rm{s}}}\\ {I_{\rm{p}}}/r_{{\rm{p}}}^2{{\ddot u}_{\rm{p}}} - {c_{{\rm{sp}}}}{{\dot x}_{{\rm{sp}}}} + {c_{{\rm{sp}}}}{{\dot x}_{{\rm{pg}}}} - {k_{{\rm{sp}}}}{x_{{\rm{sp}}}} + {k_{{\rm{p}}g}}{x_{{\rm{pg}}}} = 0\\ {I_g}/r_{{\rm{g}}}^2{{\ddot u}_{\rm{g}}} - 3{c_{{\rm{sp}}}}\cos {\alpha _{{\rm{sp}}}}{{\dot x}_{{\rm{sp}}}} - 3{c_{{\rm{pg}}}}\cos {\alpha _{{\rm{pg}}}}{{\dot x}_{{\rm{pg}}}}- \\ \quad 3{k_{{\rm{sp}}}}{x_{{\rm{sp}}}}\cos {\alpha _{{\rm{sp}}}} - 3{k_{{\rm{pg}}}}{x_{{\rm{pg}}}}\cos {\alpha _{{\rm{pg}}}} + {c_{{\rm{gs}}}}({{\dot u}_{\rm{g}}}/r_{\rm{g}}^2 - \\\quad {{\dot u}_{\rm{s}}}/{r_{\rm{g}}}{r_{\rm{s}}}) + {k_{{\rm{gs}}}}({u_{\rm{g}}}/r_{\rm{g}}^2 - {u_{\rm{s}}}/{r_{\rm{g}}}{r_{\rm{s}}}) = - {T_{{\rm{in}}}}/{r_{\rm{g}}} \end{array} \right. $$ (1) 2.2 永磁电机矢量控制模型
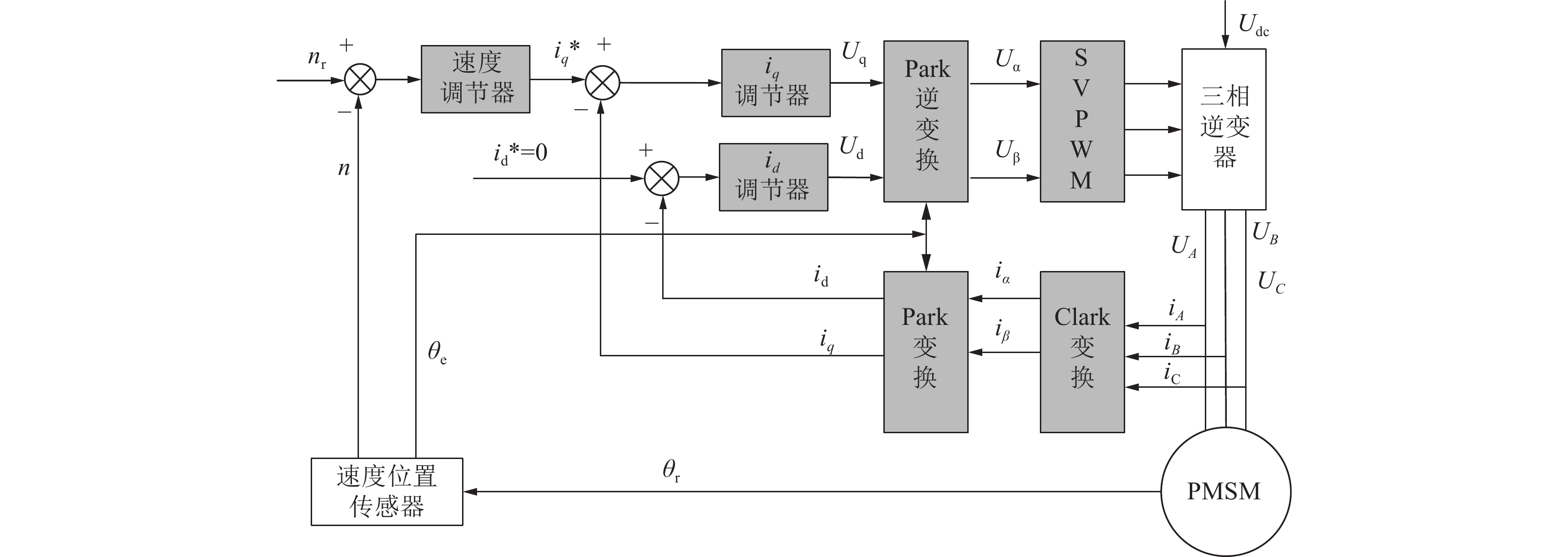
目前,永磁同步电机多采用矢量控制,基于磁场定向技术,通过坐标变换可实现励磁分量和转矩的重构及解耦,进而实现分别对电机d轴电流与q轴电流的控制,具有调速范围宽、运行平滑、动态转矩高等优点[18]。本文最终选用图7所示的基于id=0永磁电机矢量控制模型,图7中nr为需求转速,n为实时输出转速,θe为电角速度,此时永磁电机电磁转矩方程如式(2),输出电磁转矩中只有q轴永磁转矩分量,驱动系统响应速度更快,以适用刮板输送机非定常落煤工况。
$$ {T_{\mathrm{e}}} = 1.5{p_{\mathrm{n}}}{i_q}{\psi _{\mathrm{f}}} $$ (2) 式中:Te为电机电磁转矩,N∙m;pn为电机极对数,iq为q电流分量,A;ψf为磁链,Wb。
2.3 刮板输送机机械负载动力学模型
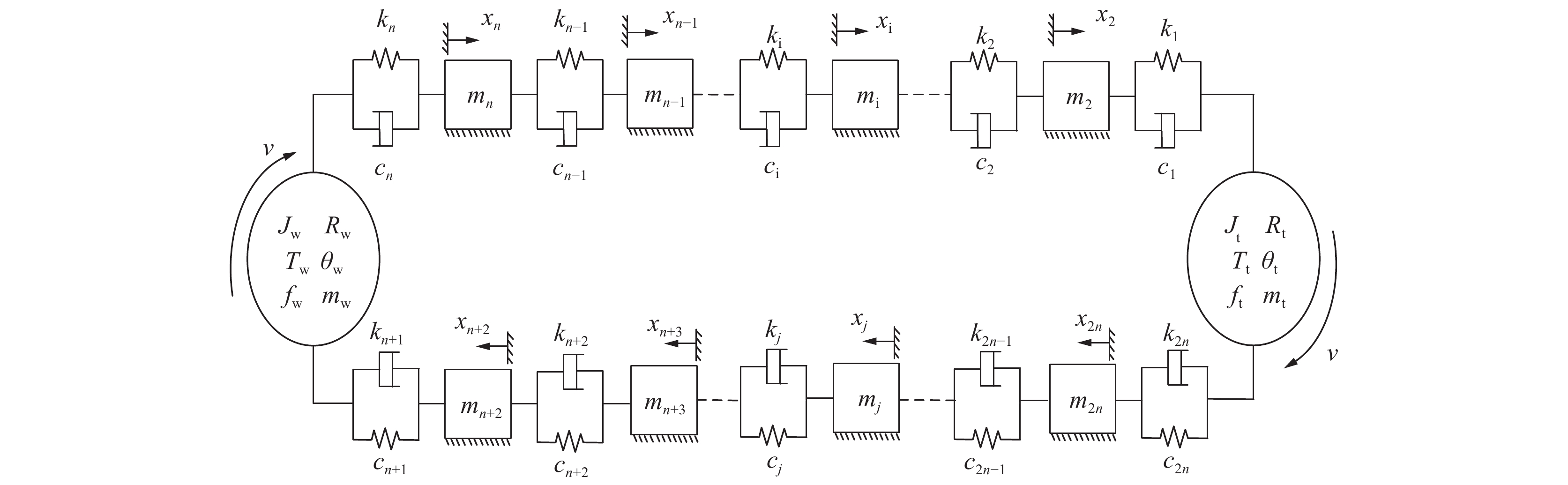
刮板输送机的机械本体主要由链轮、链条与刮板等部分组成,为简化建模过程,可将链条与刮板看作整体,等效质量沿刮板中部槽均匀分布。刮板输送机链条具有明显的黏性与弹性,对此选用Kelvin-Vogit模型作为基本动力学单元,将刮板输送机整体划分为2n个动力学单元,得到图8所示的机械负载动力学模型,并建立了式(3)所示的整机机械负载动力学方程。
图8与式(3)中Fi、ki、mi、ci、xi、$\dot x_i $、$\ddot x_i $分别代表链条的第i个动力学单元的运行阻力、刚度系数、质量、阻尼系数、位移变化量、速度变化量与加速度变化量,i的范围为1~2n;$\dot \theta_i $、$\ddot \theta_i $分别为链轮位移、速度与加速度;J、R、f、m、T分别代表转动惯量、节圆半径、附加阻力、单元体质量与电磁转矩;下标t代表机头,w代表机尾。
$$\begin{aligned} \left\{ \begin{gathered} {J_{\text{t}}}{{\ddot \theta }_{\text{t}}} + ( - {F_{2n}} + {F_1}){R_{\text{t}}} = {T_{\text{t}}} - {f_{\text{t}}}{R_{\text{t}}} \\ {J_{\text{w}}}{{\ddot \theta }_{\text{w}}} + ( - {F_n} + {F_{n + 1}}){R_{\text{w}}} = {T_{\text{w}}} - {f_{\text{w}}}{R_{\text{w}}} \\ {m_2}{{\ddot x}_2} + ({F_2} - {F_1}) = - {f_2} \\ {m_i}{{\ddot x}_i} + ({F_{i + 1}} - {F_i}) = - {f_i} \\ \qquad \qquad\qquad\vdots \\ {m_{2n}}{{\ddot x}_{2n}} + ({F_{2n}} - {F_{2n - 1}}) = - {f_{2n}} \\ {F_1} = {k_1}({\theta _{\text{t}}}{R_{\text{t}}} - {x_2}) + {c_1}({{\dot \theta }_{\text{t}}}{R_{\text{t}}} - {{\dot x}_2}) \\ {F_i} = {k_i}({x_i} - {x_{i + 1}}) + {c_1}({{\dot x}_i} - {{\dot x}_{i + 1}}) \\ {F_{2n}} = {k_{2n}}({x_{2n}} - {\theta _{\text{t}}}{R_{\text{t}}}) + {c_{2n}}({{\dot x}_{2n}} - {{\dot \theta }_{\text{t}}}{R_{\text{t}}}) \\ {x_i} = {\theta _{\text{t}}} \\ {x_{n + 1}} = {\theta _{\text{w}}} \\ \end{gathered} \right. \end{aligned} $$ (3) 2.4 机−电耦合动力学仿真模型
为构建机−电耦合动力学模型,将式(3)变换为矩阵方程形式:
$$ {\boldsymbol{M \ddot x}} + {\boldsymbol{C\dot x}} + {\boldsymbol{Kx}} ={\boldsymbol{F}} $$ (4) 式中:F为外力矩阵;M为质量矩阵;C为阻尼矩阵;K为刚度矩阵;x为刮板输送机链条位移矩阵;$ {\boldsymbol{\dot{x} }}$为刮板输送机链条速度矩阵;${\boldsymbol{ \ddot{x}}} $为刮板输送机链条加速度矩阵。
选取刮板输送机的链条位移变化量xi作为系统状态向量,可进一步得到基于状态空间方程的永磁半直驱刮板输送机机电耦合动力学方程:
$$ \left\{\begin{array}{l}{\boldsymbol{\dot{V}}}={\boldsymbol{AV}}+{\boldsymbol{BU}}\\ {\boldsymbol{y}}={\boldsymbol{CV}}+{\boldsymbol{DU}}\\ {\boldsymbol{V}}=[{x}_{1}\text{, }{x}_{2}\text{, }\cdots {x}_{2{n}}\text{, }{\dot{x}}_{1}\text{, }{\dot {x}}_{2}\text{, }\cdots {\dot{x}}_{2{n}}]\end{array}\right. $$ (5) 式中:
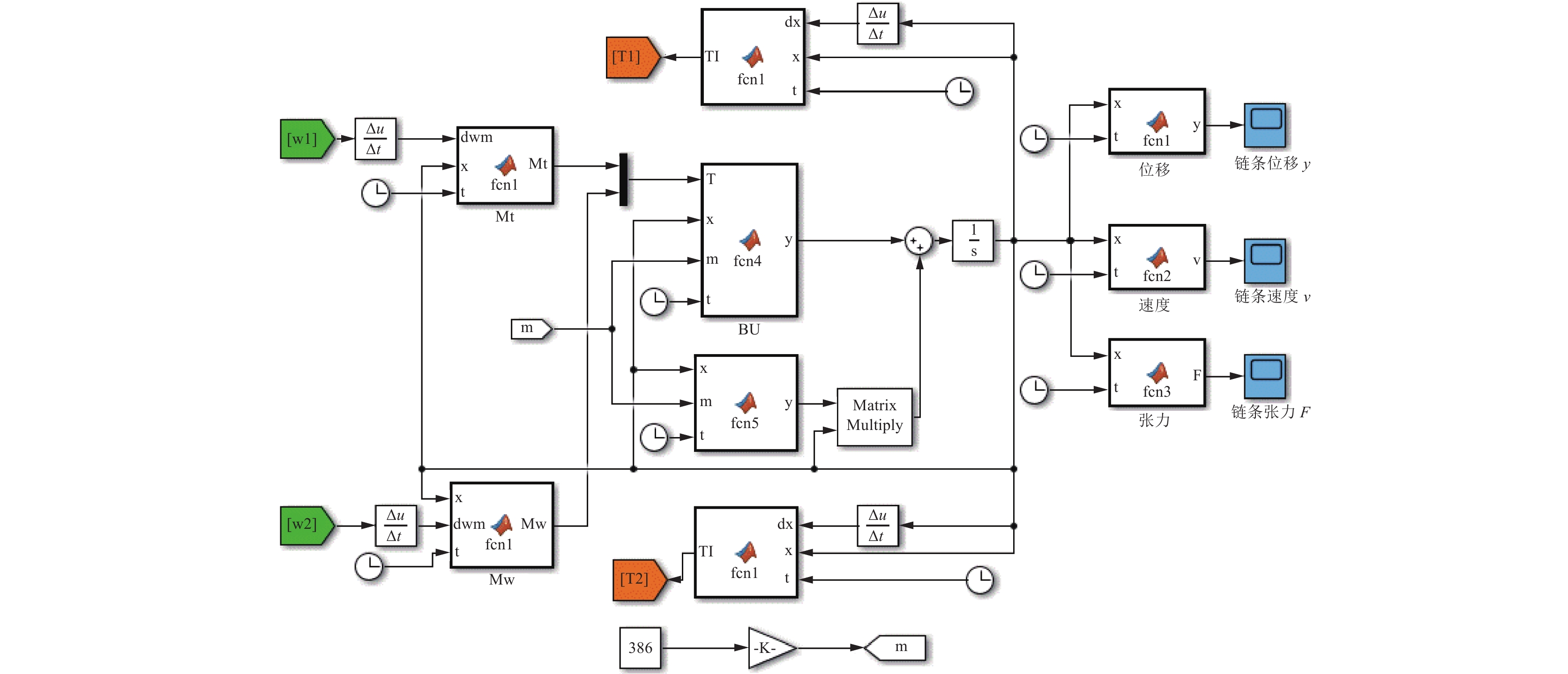
$$ \left\{\begin{array}{l}状态矩阵:{\boldsymbol{A}}=\left[\begin{array}{cc}0& I\\ -{M}^{-1}K& {M}^{-1}F\end{array}\right]\text{ }\\ 输入矩阵:{\boldsymbol{B}}=\left[\begin{array}{c}0\\ {M}^{-1}F\end{array}\right]\\ 输入矩阵:{\boldsymbol{C}}=\left[\begin{array}{ccc}1& 0& 0\\ 0& \ddots & 0\\ 0& 0& 1\end{array}\right]\\ 直连矩阵:{\boldsymbol{D}}=[0]\end{array}\right. $$ 基于式(5),采用MATLAB/Simulink软件搭建永磁半直驱刮板输送机的机−电耦合动力学仿真模型。如图9所示,该模型边界条件为电机转速n及承载端单元装载煤流质量m。
3. 永磁电机半直驱刮板输送机的机−电耦合动力学行为仿真试验
基于永磁电机半直驱刮板输送机的机−电耦合动力学模型,对刮板输送机整机空载启动后平稳落煤、非定常落煤、满载启动等3种运行工况以及齿轮传动系统在冲击载荷下的动力学行为进行仿真分析。以表2所示的永磁电机半直驱系统关键参数作为设计目标,通过Maxwell仿真得到了永磁电机的关键性能参数,将其作为表3所示的机−电耦合动力学模型的仿真参数。
表 3 机−电耦合动力学模型仿真参数Table 3. Simulation parameters of electromechanical coupling dynamics model参数 数值 定子电阻/Ω 0.0816 永磁体磁链/Wb 5.7 直轴电感/mH 10.2 交轴电感/mH 37.9 电机转动惯量/(kg·m2) 40 阻尼系数/(N·m·s) 0.005 系统额定转速/(r·min−1) 50 链条转速/(m·s−1) 2 3.1 空载启动后平稳落煤工况仿真分析
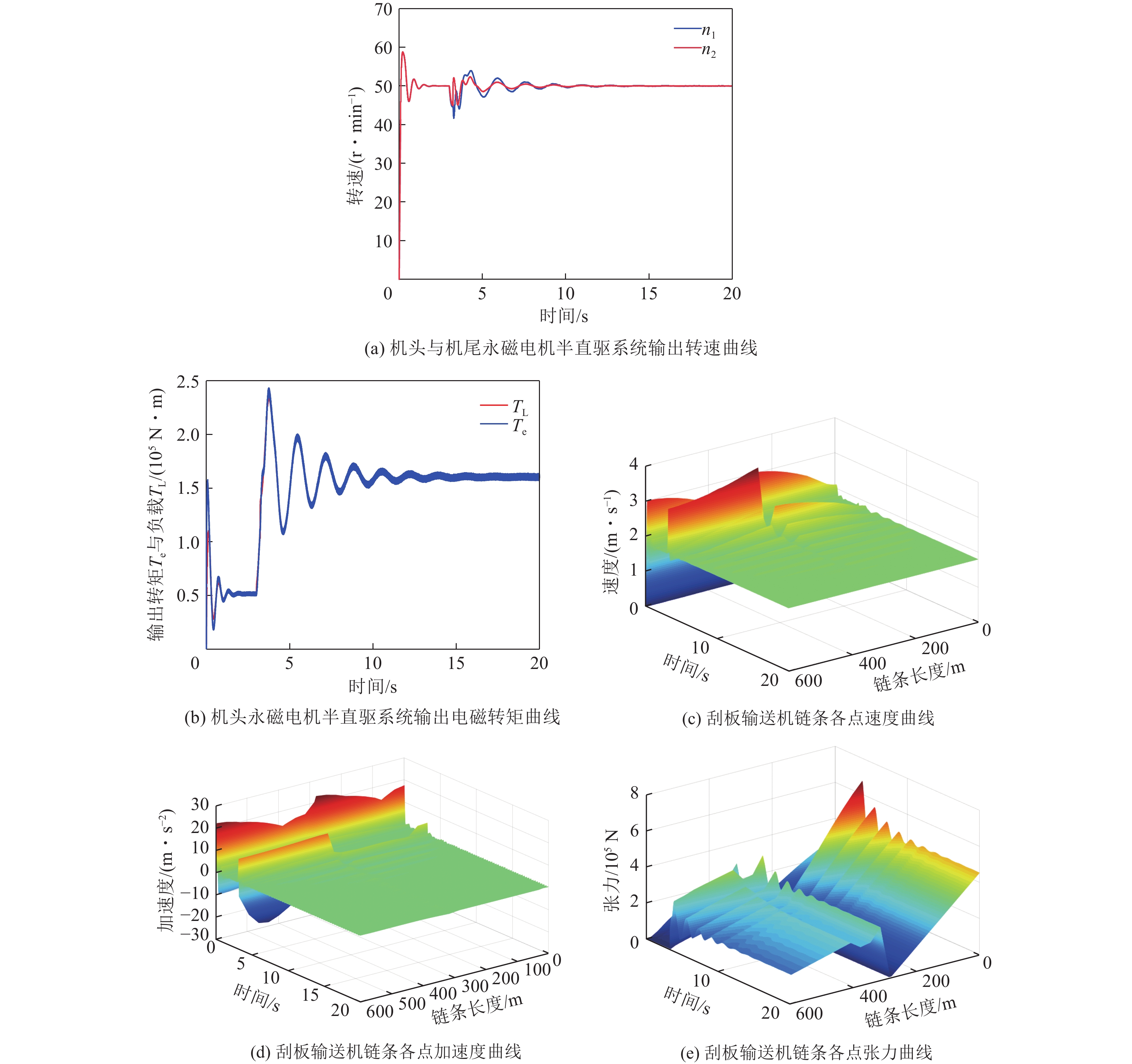
如式(6)所示,为模拟空载启动后平稳落煤工况,设置承载端单元装载煤流质量m为边界条件,在前3 s空载启动完成后,第4 s起切换至恒定负载落煤运行工况,设置仿真时间为20 s,得到图10所示仿真结果。
$$ m(t) = \left\{ \begin{gathered} 0\quad (t < {\text{3)}} \\ 386 \quad (t \geqslant {\text{3)}} \\ \end{gathered} \right. $$ (6) 机头与机尾永磁电机半直驱系统输出转速曲线如图10a所示。系统空载启动,在0.2 s最大超调量接近60 r/min,在2 s左右达到额定设定转速50 r/min;在第4 s平稳落煤后,永磁电机半直驱系统转速在40 ~55 r/min的范围内波动;两台电机转速变化趋势基本保持一致,在12 s左右恢复至额定转速。这表明,永磁电机半直驱系统在空载与负载突变下均能保持良好的速度响应特性。
机头永磁电机半直驱系统输出电磁转矩曲线如图10b所示。为克服刮板输送机链条与刮板在中部槽上受到的运行阻力,永磁电机半直驱系统空载启动最大转矩升至1.6×105 N·m,经过2 s后稳定在5×104 N·m;在第4秒平稳落煤后,系统负载转矩突变显著增加,为克服煤炭运输阻力,永磁电机半直驱系统电磁转矩在短时间内突增至2.4×105 N·m,最终稳定至1.6×105 N·m;在空载启动与平稳落煤过程,机头永磁电机半直驱系统的输出驱动转矩与负载转矩曲线保持一致,也进一步表明了新型永磁电机半直驱系统良好的拖动性能,能够满足拖动不同负载的需求。
输送机运输距离300 m,因此承载段与空回段链条长度共计600 m,为分析刮板输送机链条各位置的动力学行为,将链条的速度、加速度与张力值作为分析对象,得到了图10c—图10d所示刮板输送机链条各点的速度、加速度变化曲线,可知,第1秒与第4秒刮板输送机在空载启动与平稳落煤下链条受到冲击,导致了链条的速度与加速度出现2次明显波动。在空载启动时链条的承载段与空回段均存在明显波动,链轮与链条的啮合点处的速度与加速度最大,分别升至3 m/s与25 m/s2,且距离机头与机尾越远,链条速度与加速度越小;而在第4秒平稳落煤导致负载突变时,承载段的链条波动要远小于空回段,最大波动速度与波动加速度分别升至3.5 m/s与15 m/s2。
刮板输送机链条各点的张力变化曲线如图10e所示。在空载启动阶段,刮板输送机在机头链轮与机尾链轮处受到的张力最大,距离链轮的啮合点越远,张力越小,其中最大张力为2.8×105 N,出现在机头链轮与链条啮合处;在平稳落煤阶段,链条受到的运输阻力远大于启动阶段,最大张力为6.5×105 N,且承载段张力值明显大于空回段,呈现周期性变化规律。
3.2 非定常落煤工况仿真分析
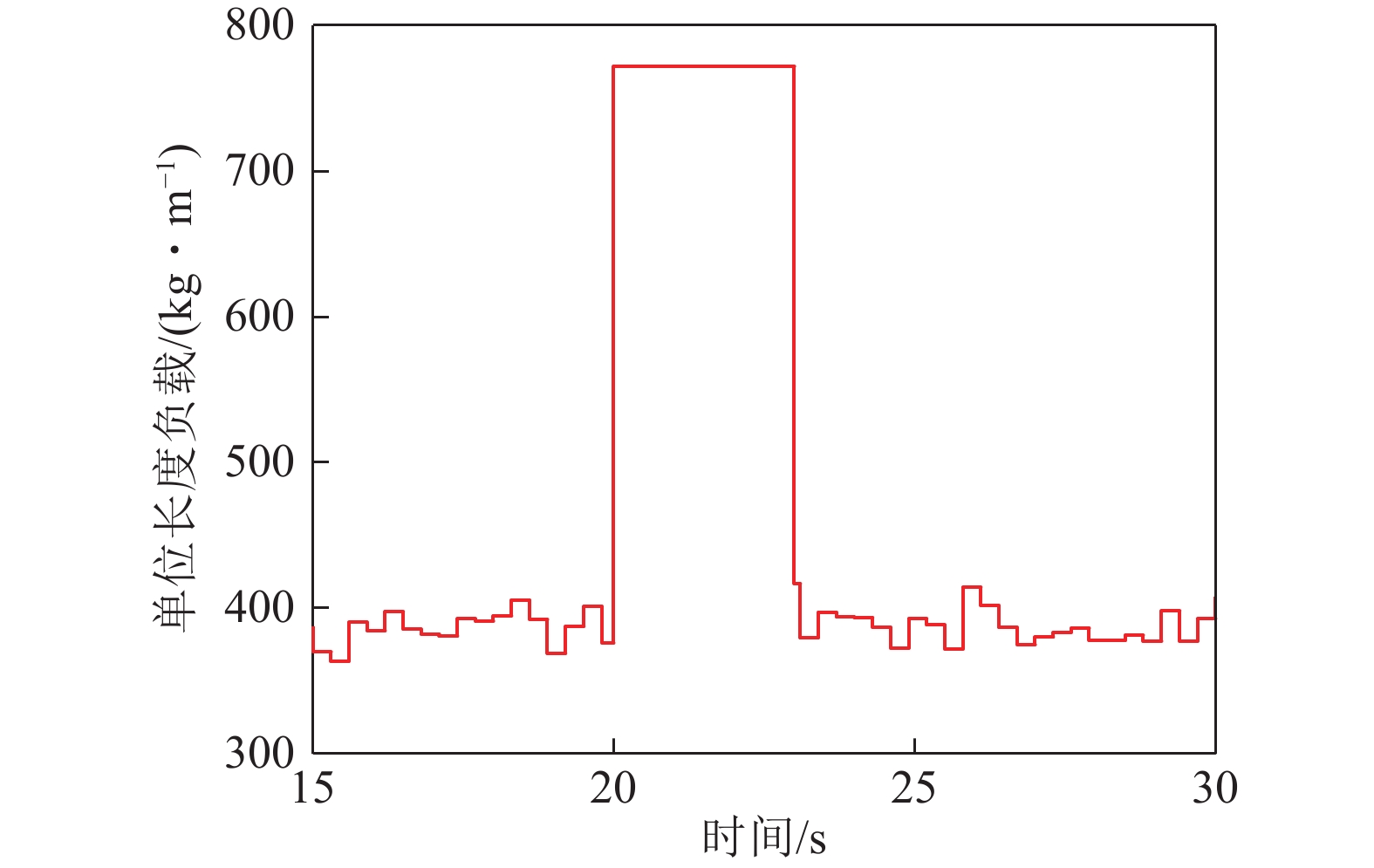
为模拟刮板输送机非定常落煤工况,设置图11所示的非定常落煤模拟曲线为边界条件m,仿真结果如图12所示。
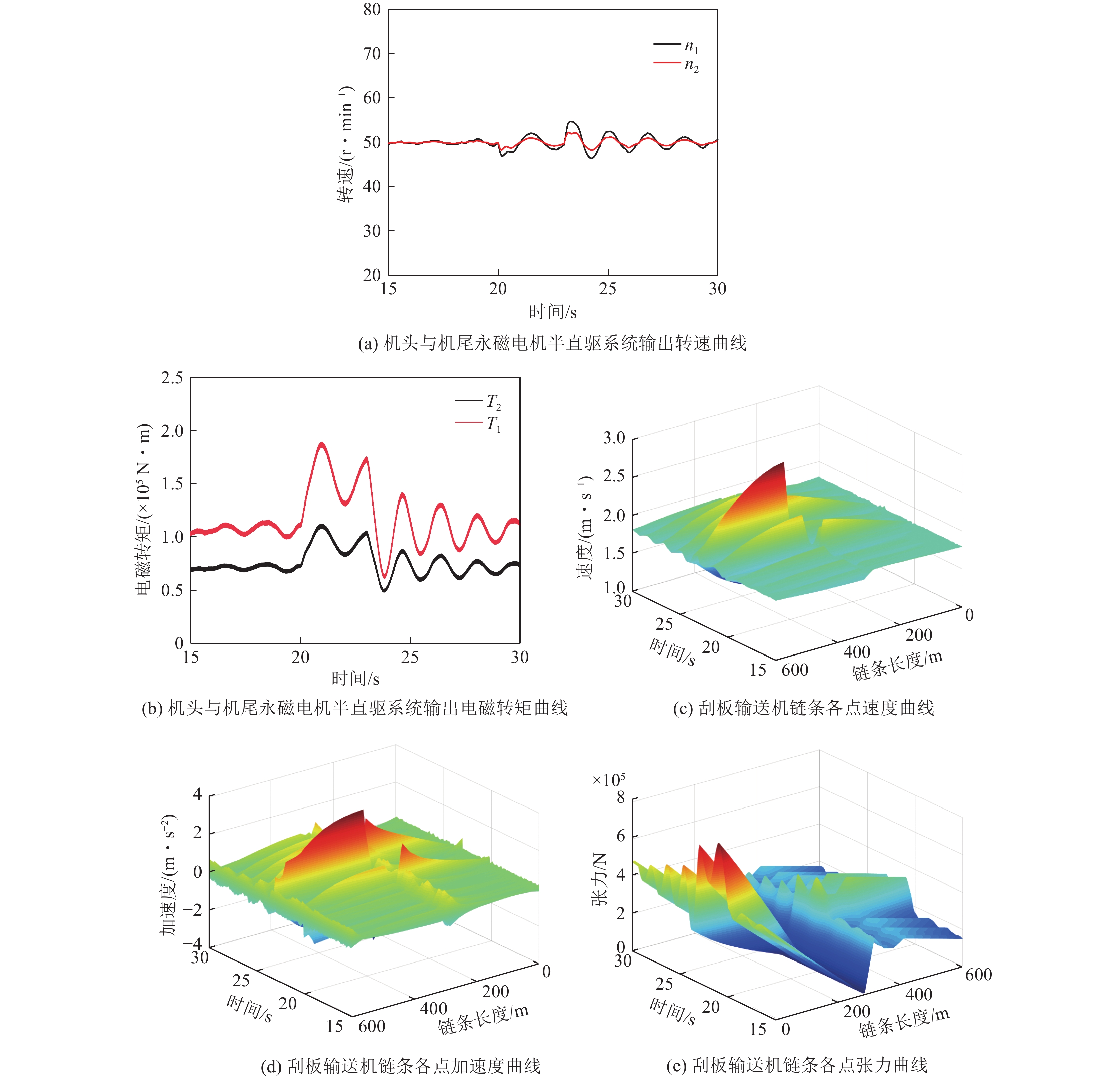
机头与机尾永磁电机半直驱系统输出转速曲线如图12a所示。在非定常落煤负载小范围波动下,永磁电机半直驱系统输出转速仍能维持在50 r/min左右;在第20秒后,系统处于2倍运输负载下,因刮板输送机运输距离长,导致物料存在堆积现象,机头电机的波动幅度要大于机尾电机。
机头永磁电机半直驱系统输出电磁转矩曲线如图12b所示。刮板输送机因机头与机尾链轮受到的负载不同,导致机头永磁半直驱电机输出电磁转矩T1大于机尾永磁半直驱电机输出电磁转矩T2。在第20秒后,在2倍负载突变下,电机的电磁转矩曲线与负载转矩曲线仍保持一致,这表明采用矢量控制策略的永磁电机半直驱系统可在2倍运输量的突变负载下平稳运行,体现了永磁电机的短时过载运行优势。
刮板输送机链条各点的速度、加速度、张力变化曲线,分别如图12c—图12e所示。在第20秒后因负载突变导致链条速度与加速度急增,最大速度约为2.7 m/s,最大加速度约为3.6 m/s2,出现在第300 m机尾链轮与承载段链条啮合点。随着运输负载突增至2倍,链条各点的张力也跟随显著增加,张力变化趋势与电磁转矩曲线基本保持一致,这是因为在负载突变时永磁电机半直驱系统所需输出电磁转矩增大,导致了对链条冲击变大,链条各点的速度、加速度与张力值也随之增加。
3.3 故障后满载启动工况仿真分析
刮板输送机在遇到故障停机后,需排查后重新启动,此时刮板输送机将处在满载启动工况,设置机电耦合动力学模型边界条件如下:
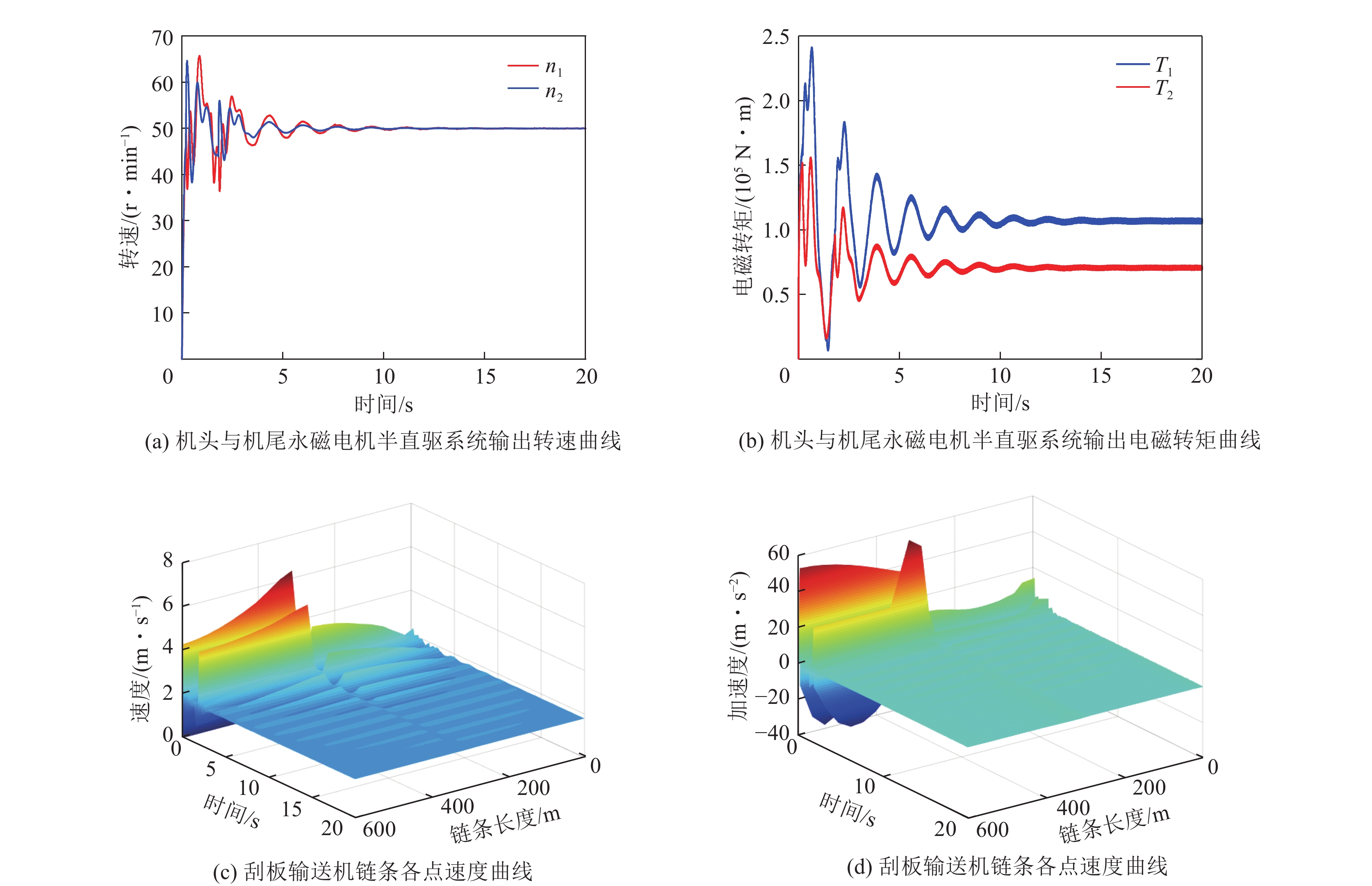
$$ m(t) = 386{\text{ kg/m (}}t \geqslant {\text{0)}} $$ (7) 机头与机尾永磁电机半直驱系统输出转速曲线如图13a所示。满载零速启动时,在前10 s刮板输送机永磁电机半直驱系统转速与电磁转矩波动要大于空载启动,最大波动转速至65 r/min,超调量为30%,是空载启动工况下的1.5倍,且因机头与机尾链轮负载情况不同,导致两台电机在最初启动阶段转速存在差值,但在前10 s后,基本恢复至50 r/min的额定转速,动态响应特性良好。
机头永磁电机半直驱系统输出电磁转矩与链条各点速度、加速度与张力变化曲线,分别如图13b—图13d所示。在满载启动工况下,永磁电机半直驱系统的电磁转矩、链条速度与加速度明显大于空载启动,其中链条峰值速度约为6 m/s,链条峰值加速度约为58 m/s2,电磁转矩峰值约为2.4×105 N·m,分别升至空载启动的2倍、2.3倍、1.6倍,这表明在满载启动下,永磁电机半直驱系统需要克服的系统惯性与运输阻力更大。
由图13c—图13d可得,在满载启动瞬间链条各点速度、加速度存在多次波动,启动时机头机尾处的链条加速度出现明显的波动,机尾处链条加速度明显高于机头部。因为机尾电机启动,带动机头链轮的转动。链条是一个粘弹性体,在加速度传递过程中出现损耗,导致机头部加速度远小于及尾部。而波动会随着时间逐渐衰减,在第10 s后链条各点的速度可维持在额定链速1.8 m/s,加速度减小至0,表明系统已进入稳定运行状态,这与电机动态特性规律基本保持一致;与空载启动工况相对比,在满载启动工况下,链条各点速度、加速度在空回段波动更为明显,这是因为满载工况下刮板输送机承载段的中部槽内已被煤炭覆盖,对链条具有一定缓冲作用,而空回段链条运输阻力明显小于承载段,导致了在负载突变时链条速度与加速度变化更为明显。
3.4 冲击载荷下齿轮传动系统仿真分析
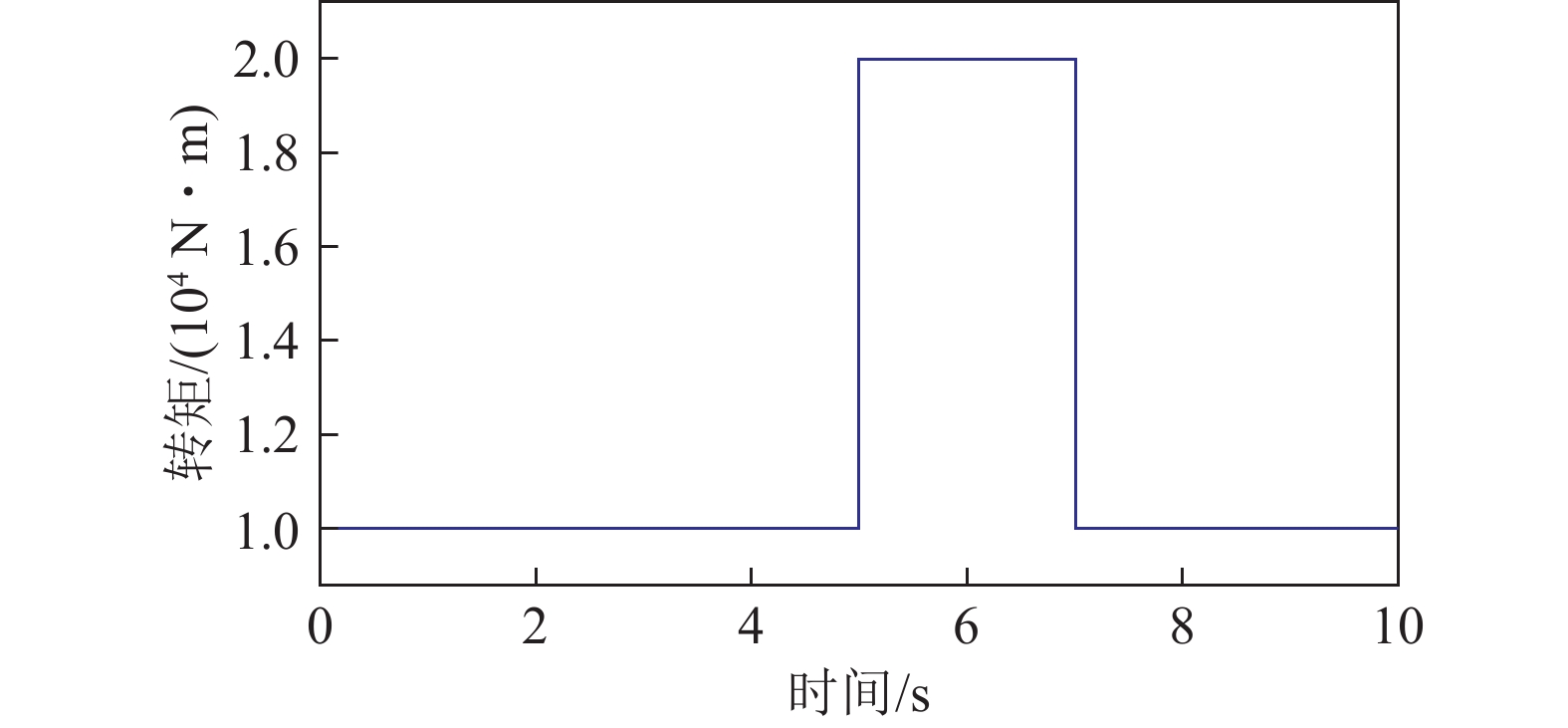
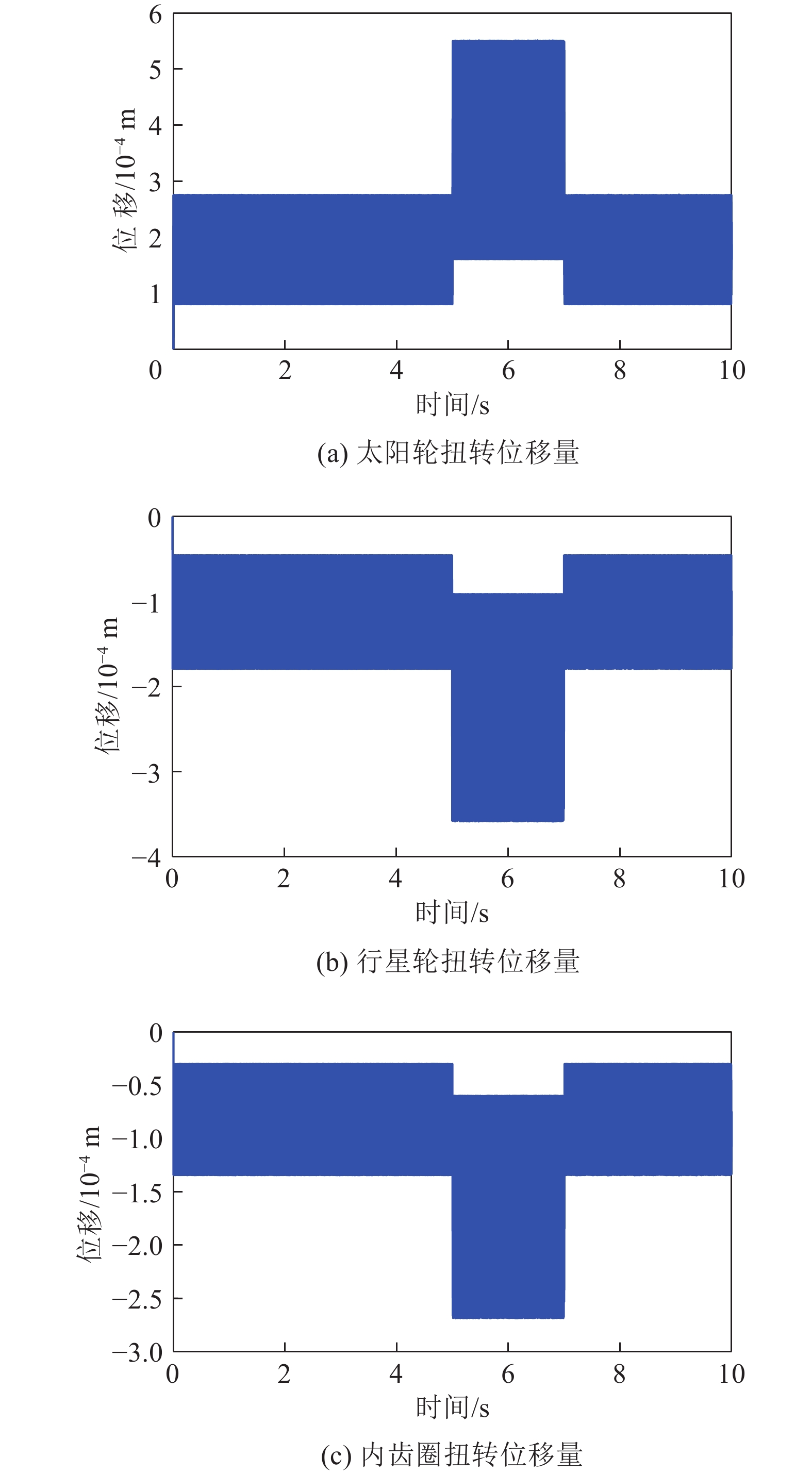
进一步,对机−电耦合动力学模型施加如图14所示的冲击载荷,可研究冲击载荷下各级齿轮的扭转位移、弹性变形与动态啮合力等动力学行为。图中的负值表示与物理坐标系方向相反。
冲击载荷作用下第一级齿轮扭转位移曲线如图15所示。在第5秒受到冲击载荷后,第一级行星轮系各齿轮扭转位移迅速增加,其中太阳轮、行星轮与内齿圈的扭转位移上升峰值分别为5.5×10−4、−3.5×10−4与−2.7×10−4 m,与起始状态相比较,分别上升了49%,48.6%与33.3%。这表明,在冲击载荷下,第一级太阳轮作为系统的输入轮,与行星轮之间产生的扭转位移峰值较大,响应速度较快。
因相同冲击载荷下第二级齿轮扭转位移变化规律与第一级类似,为此通过表4的数据来简化表述冲击载荷下第二级齿轮扭转位移变化情况。
表 4 冲击载荷下第二级齿轮扭转位移Table 4. Second stage gear torsional displacement under impact load参数名称 扭转位移量变化范围/m 太阳轮 3.0×10−4~9.2×10−4 行星轮 −1.0×10−4~−6.9×10−4 内齿圈 −2.1×10−4~−6.9×10−4 由表4可得,在第5秒发生突变时,第二级太阳轮、行星轮与内齿圈的扭转位移变化范围分别为6.2×10−4、5.9×10−4与4.8×10−4 m,在数值上明显大于第一级行星轮系。这表明,永磁电机半直驱系统内部行星齿轮减速装置的扭转位移是连续传导,在冲击载荷下,距离输入端越远,扭转位移越明显。
由于齿轮传动系统的扭转位移与弹性变形为线性关系,而齿轮间的动态啮合力为齿轮副沿啮合线的弹性变形与平均啮合刚度的乘积,因此冲击载荷下齿轮弹性变形与动态啮合力变化趋势均与图14一致,对此可通过表5与表6的数据来简化表述齿轮弹性变形与动态啮合力变化情况。
表 5 冲击载荷下行星齿轮传动系统弹性变形量Table 5. Elastic deformation of planetary gear transmission system under impact load参数名称 弹性变形量变化范围/m 第一级太阳轮与行星轮 1.8×10−4~4.4×10−4 第一级内齿圈和行星轮 1.5×10−4~6.1×10−4 第二级太阳轮与行星轮 3.8×10−4~7.9×10−4 第二级内齿圈与行星轮 3.5×10−4~12.3×10−4 表 6 冲击载荷下行星齿轮传动系统动态啮合力Table 6. Dynamic meshing force of planetary gear transmission system under impact load参数名称 动态啮合力变化范围/N 第一级太阳轮与行星轮 1.7×105~4.6×105 第一级内齿圈和行星轮 1.3×105~5.8×105 第二级太阳轮与行星轮 5.9×105~1.2×106 第二级内齿圈与行星轮 5.0×105~1.7×106 由表5可得,在冲击载荷下,第一级、第二级太阳轮与行星轮之间的弹性变形量的变化范围分别为2.6×10−4、4.1×10−4 m,而第一级、第二级内齿圈与行星轮之间的弹性变形量的变化范围分别为4.6×10−4、8.8×10−4 m。这表明,在冲击载荷下,内齿圈与行星轮之间的弹性变形要比太阳轮与行星轮之间产生的弹性变形更为明显。同时,第二级行星轮系的弹性变形量也明显大于第一级行星轮系,这与冲击载荷下第一级与第二级轮系扭转位移变化规律一致。
由表6可得,在第5秒冲击载荷下,第一级、第二级太阳轮与行星轮之间的动态啮合力峰值分别为4.6×105、1.2×106 N,而第一级、第二级内齿圈与行星轮之间的动态啮合力峰值分别为5.8×105、1.7×106 N。这表明,第二级行星齿轮系的动态啮合力大于第一级行星齿轮系的的动态啮合力,基本动力学规律也与弹性变形量规律相一致。
4. 刮板输送机永磁电机半直驱系统台架试验
煤矿井下综采工作面刮板输送机的运输工况恶劣,其驱动电机须通过防爆检测与安标认证,而目前因缺乏针对新型永磁电机半直驱系统的整机检验标准,鲜有针对刮板输送机运输工况的防爆永磁电机半直驱系统产品。因此,本研究通过在实验室搭建永磁电机半直驱系统试验平台,借助测功机模拟刮板输送机运输工况,开展永磁电机半直驱系统驱动性能试验,从台架试验方面探究新型永磁电机半直驱系统的优势。
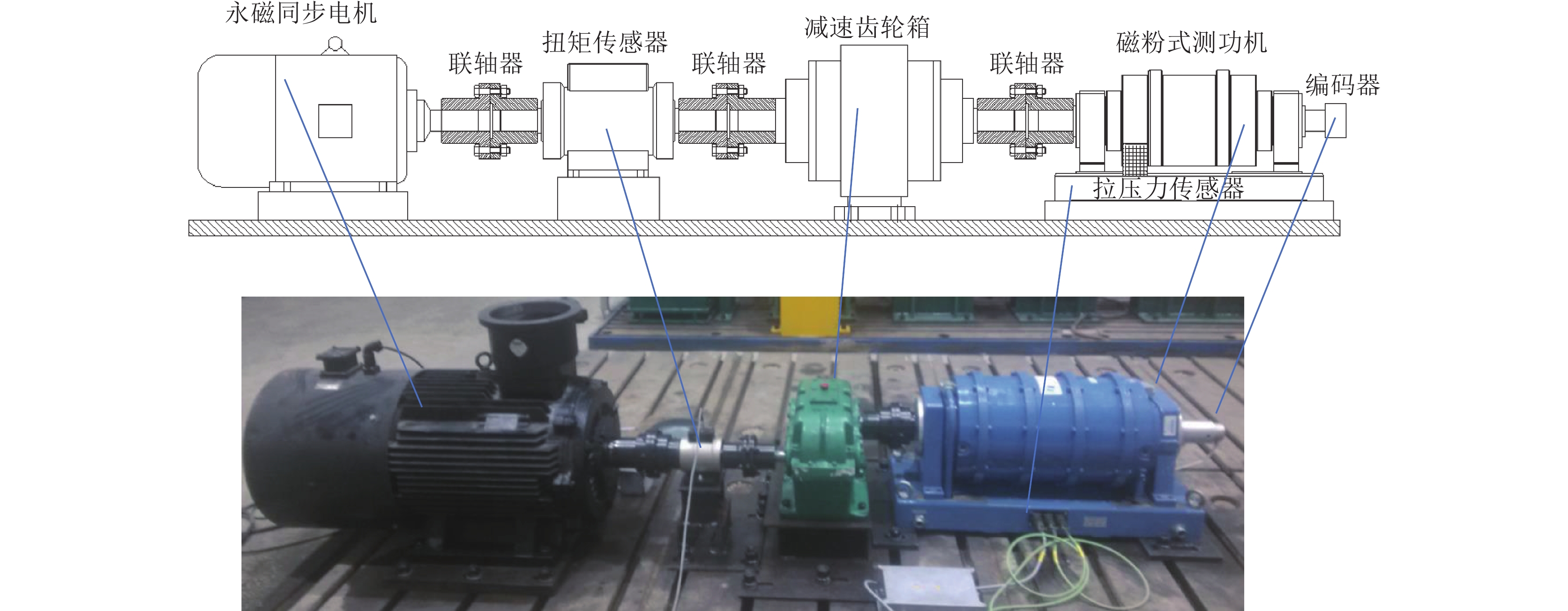
4.1 永磁电机半直驱系统试验平台搭建
为验证永磁电机半直驱系统的动态特性,搭建了永磁电机半直驱系统试验平台(图16),采用“永磁同步电机+二级齿轮减速器”来等效替代永磁电机半直驱系统。为使试验平台能够准确地模拟永磁电机半直驱系统的负载特性,进而探究新型永磁电机半直驱系统的优势,需对永磁电机半直驱系统的各个部分物理量进行等效缩放,忽略永磁电机半直驱系统中摩擦力的影响,可以将永磁电机半直驱系统的负载方程写为:
$$ J_{{\mathrm{m}}}^{*}=\dfrac{{\mathrm{d}} \omega_{{\mathrm{m}}}^{*}}{{\mathrm{d}} t}=T_{{\mathrm{e}}}^{*}-T_{{\mathrm{L}}}^{*} / i $$ (8) 式中:$ {J}_{{\mathrm{m}}}^{*} $为系统转动惯量;$ {\omega }_{{\mathrm{m}}}^{*} $为系统输出转速;$ {T}_{{\mathrm{e}}}^{*} $为系统电磁转矩;$ {T}_{{\mathrm{L}}}^{*} $为刮板输送机负载转矩;i为行星齿轮减速机构的减速比15。
永磁电机半直驱系统对用的标幺值系统负载方程为:
$$ J_{{\mathrm{m}}}=\frac{{\mathrm{d}} \omega_{{\mathrm{m}}}}{{\mathrm{d}} t}=T_{{\mathrm{e}}}-T_{{\mathrm{L}}}/ i $$ (9) 式中:Jm、ωm、Te、TL分别为$ {J}_{{\mathrm{m}}}^{*} $、$ {\omega }_{{\mathrm{m}}}^{*} $、$ {T}_{{\mathrm{e}}}^{*} $、$ {T}_{{\mathrm{L}}}^{*} $的标幺值,即小比例模拟系数。因试验平台所用的二级齿轮减速机构减速比为8,故i*=i×15/8,从而克服减速比不同,实现等参数缩放。
刮板输送机的动态载荷可通过试验平台的磁粉式测功机来模拟,试验平台具体参数见表7。
表 7 永磁电机半直驱系统试验平台参数Table 7. Parameters of permanent magnet motor semi-direct driving system test platform设备 型号 永磁同步电机 TYVZ-3800-280M-16 磁粉式测功机 4PB15 测功机控制器 DSP6001 二级齿轮减速器 ZLY160-8-1 扭矩传感器 TQ-660 数据采集卡 USB-7648A 4.2 空载启动后平稳落煤试验
为模拟空载启动后平稳落煤试验,采用等效缩放原则,在4PB15磁粉式测功机内设置图17所示输出负载转矩,该曲线与图10b基本一致。对处理后的机头负载进行再处理,满足磁粉测功机的加载要求。
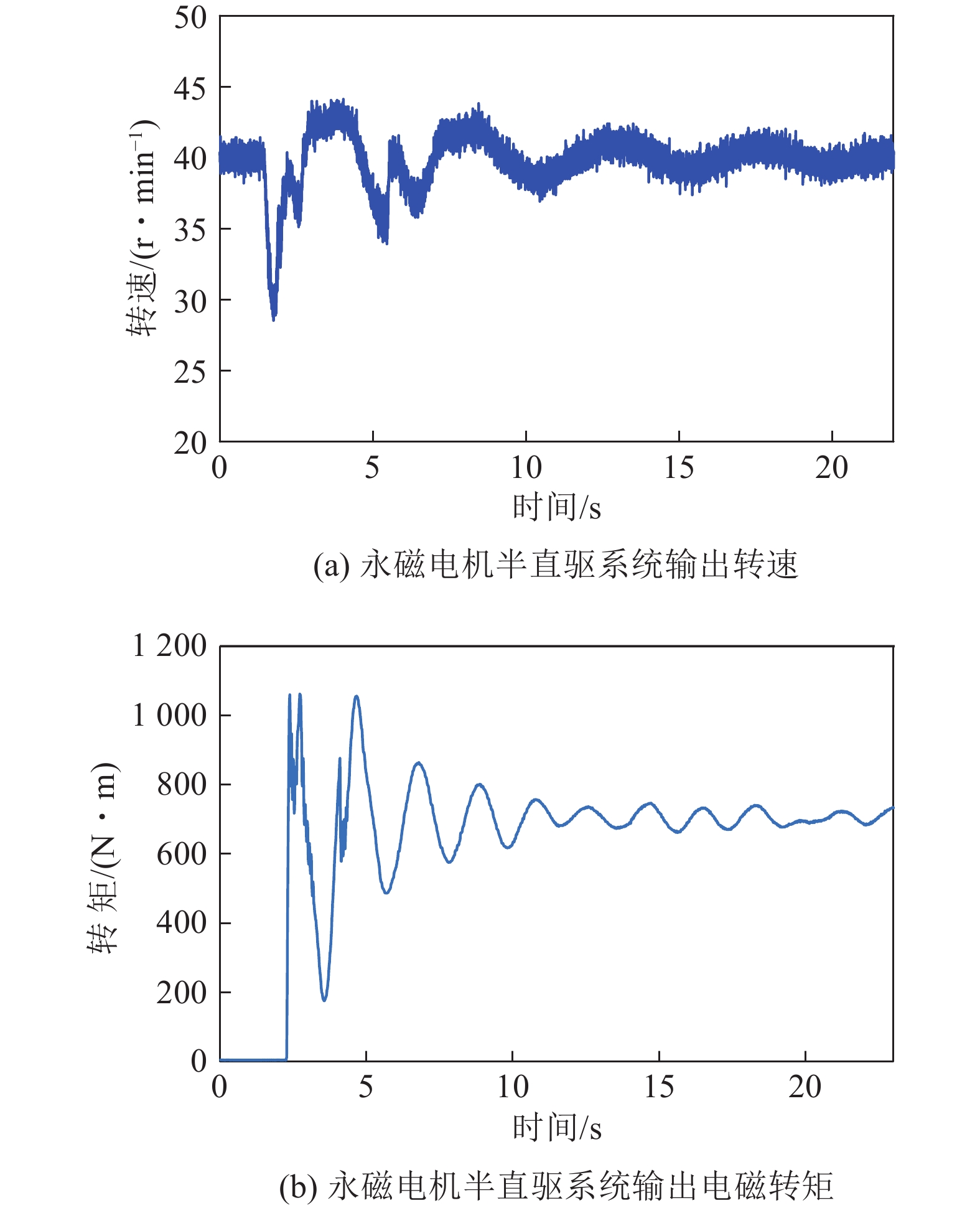
设置试验时间为30 s,收集轴端编码器数据,可绘制得到图18a所示的永磁电机半直驱系统输出转速曲线。在磁粉测功机负载转矩变化下,永磁电机半直驱系统输出转速在额定转速40 r/min附近波动;在第5 s平稳落煤时,转速突变明显,但仅需15 s系统即可恢复稳定运行状态。这表明,永磁电机半直驱系统具有良好的动态响应特性与抗干扰能力。
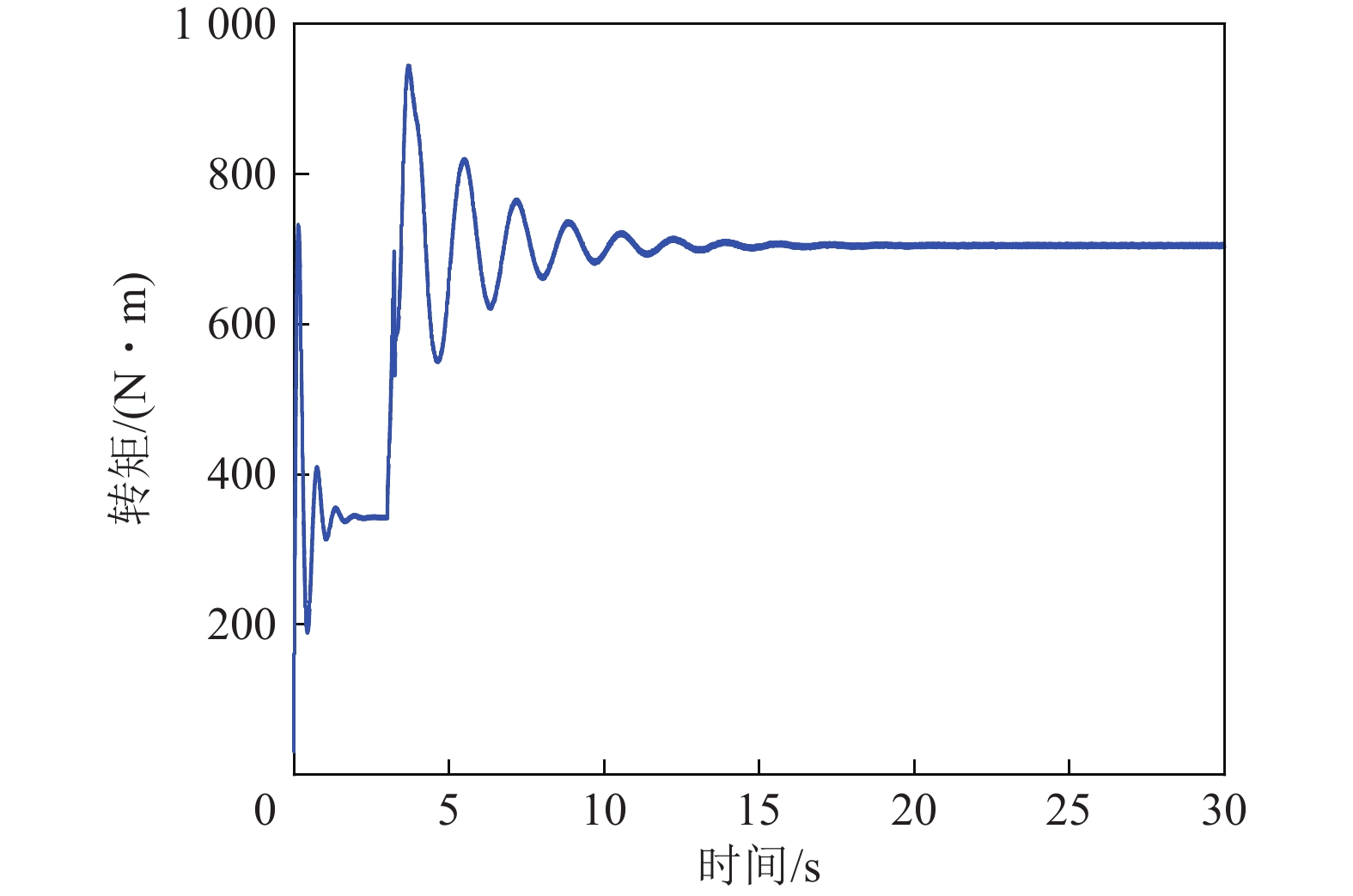
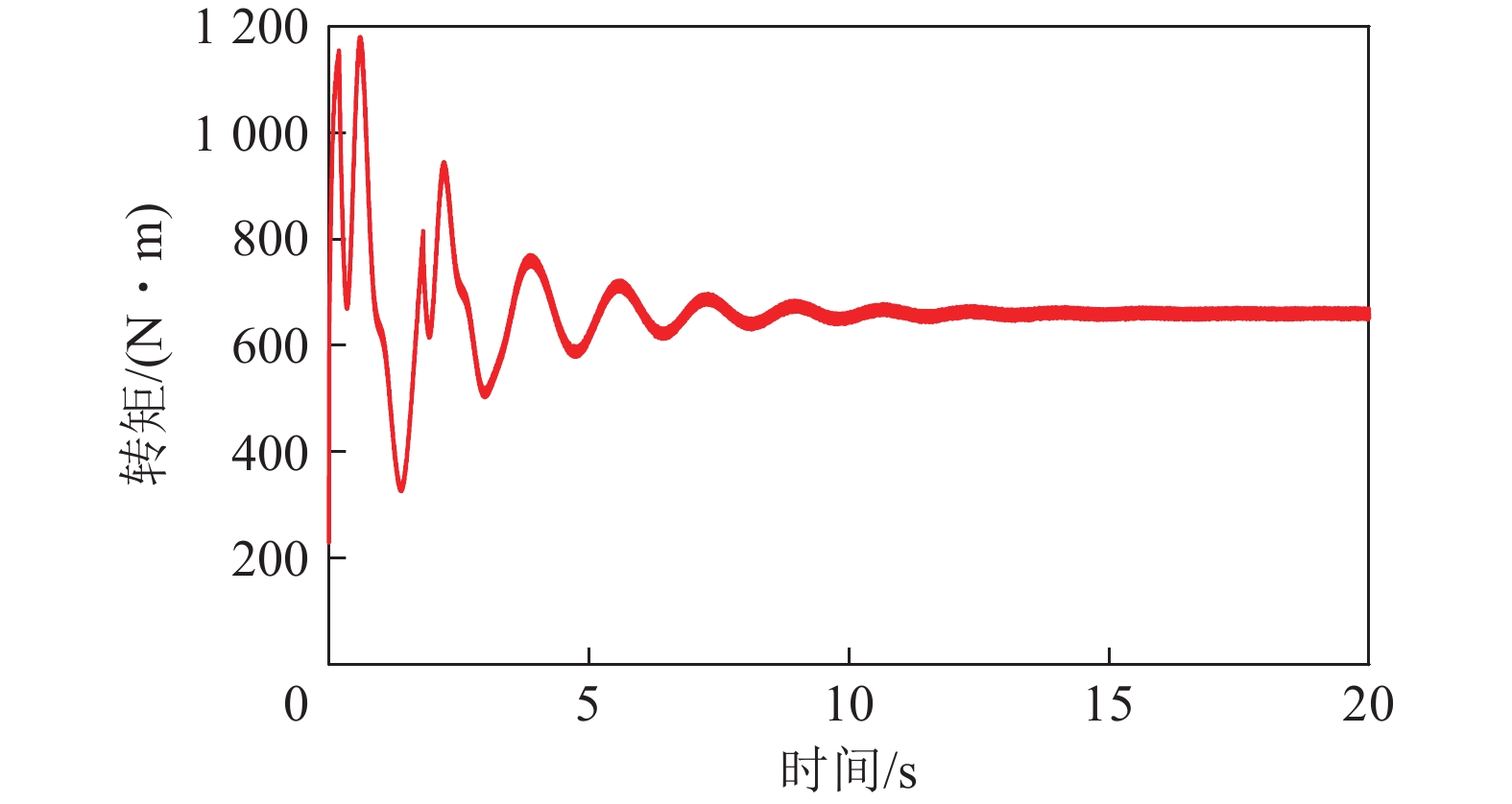
永磁电机半直驱系统输出电磁转矩曲线如图18b所示。除缓冲时间外,该曲线在数值与变化趋势上与图17基本保持一致。这表明,永磁电机半直驱系统能够应对负载突变,具有良好的低速大扭矩输出特性。
4.3 重载启动试验
为模拟永磁电机半直驱系统故障后直接重载启动的特性,可采用图19所示的负载转矩曲线进行试验。为避免永磁电机半直驱系统与测功机受到大负载冲击,在测功机中增加2 s零负载时间,绘制得到图20所示的满载启动工况下系统输出特性。
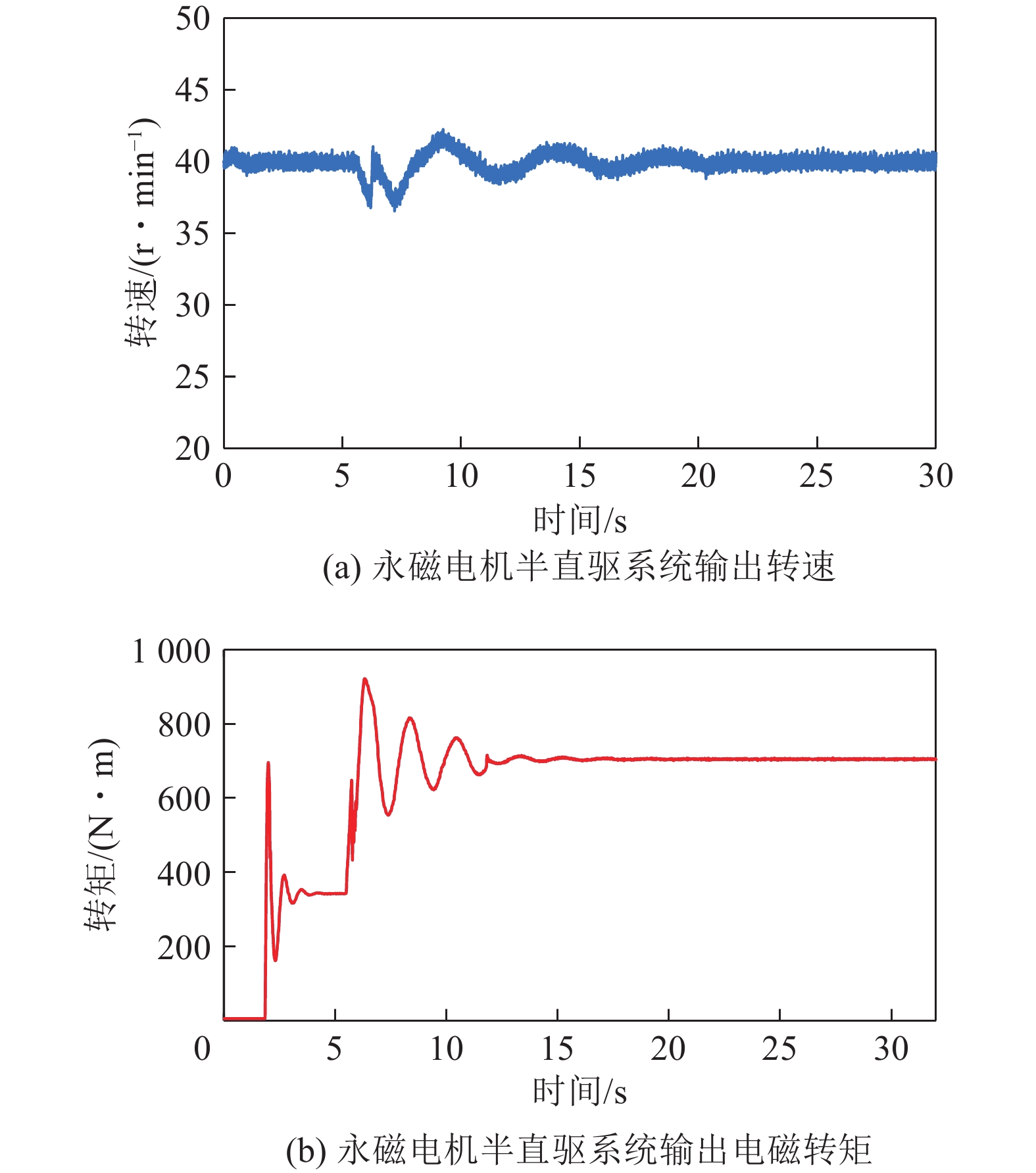
永磁电机半直驱系统输出转速曲线如图20a所示。与空载启动工况对比,零速重载启动工况下永磁电机半直驱系统的转速在29~43 r/min范围内波动,波动幅度更大,但也仅需15 s系统输出转速即可稳定至40 r/min附近。这表明,永磁电机半直驱系统具有良好的零速重载启动特性。
永磁电机半直驱系统输出电磁转矩曲线如图20b所示。负载突变瞬间,系统转速会瞬间降低,在id=0双闭环矢量控制策略作用下,系统的q轴输出电流会瞬间增加,使得永磁电机输出电磁转矩能够与负载转矩曲线保持一致。
基于以上台架试验结果可得:试验得到的永磁电机半直驱系统输出转速与电磁转矩变化规律,与前文机−电耦合动力学模型的电机动态特性仿真试验结果基本一致。
5. 永磁电机半直驱系统与异步电机驱动系统的驱动性能对比分析
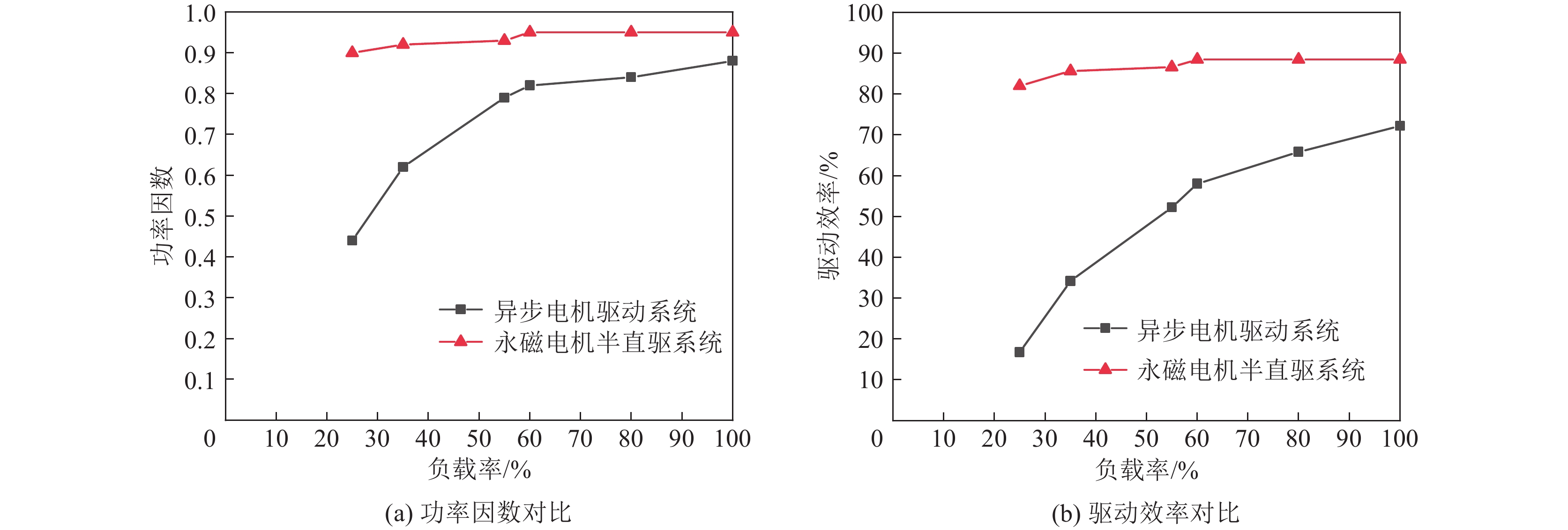
为进一步对比分析永磁电机半直驱系统驱动性能的优势,本研究选取不同负载率下电机功率因数与驱动效率作为关键性能指标,其中功率因数与电机耗电量直接相关,驱动效率则是衡量电机驱动性能的重要指标。对此,以永磁电机半直驱系统试验平台上的37 kW永磁同步电机为测试对象,分别采集25%、35%、55%、60%、80%与100%负载率下永磁同步电机的参数,将其与由“隔爆型三相异步电机+液力耦合器+减速器”组成的37 kW异步电机驱动系统进行对比,其中:减速器传动效率选取98%,液力耦合器传动效率选取96%。通过计算,得到如图21所示的结果。
永磁电机半直驱系统与传统异步电机驱动的功率因数对比曲线如图21a所示。异步电机驱动系统功率因数与负载率呈正相关变化,在25%负载率下功率因数仅为44%,而在煤矿井下综采工作面刮板输送机运行工况较为恶劣,经常处在动态落煤下运行,异步电机为保证大启动转矩,在选型时也会刻意提高功率富裕量,存在“大马拉小车”现象,因而传统异步电机驱动系统会持续运行在低功率因数区间,造成严重电能浪费。相比较而言,永磁电机半直驱系统采用永磁体励磁,无需转子励磁绕组,因此不仅功率因数要明显大于异步电机驱动系统,平均高达90%以上,而且由于定子绕组几乎为纯阻性负载,导致功率因数基本不受负载率变化影响,可持续在高效区间运行。
基于电机各负载点功率因数值,电机、减速器与液力耦合器传动效率值,可得到图21b所示的驱动效率对比曲线。永磁电机半直驱系统的传动效率在各负载率点均维持在82%~88%,而异步电机系统的驱动效率与负载率呈现正相关变化,在25%负载率下驱动效率仅为16%,与永磁电机半直驱系统驱动效率差异高达65.3%,平均驱动效率差异为36.7%,即使在满负载率下也相差16.3%,存在严重电能浪费。
因此,在相同负载下,采用永磁电机半直驱系统可显著提高刮板输送机的功率因数与驱动效率,大幅度减少设备用电量,更具节能减碳效益。
6. 结 论
1)通过仿真试验与台架试验表明,基于id=0双闭环矢量控制策略的新型永磁电机半直驱系统,通过内置行星齿轮减速机构,在缩小电机体积的同时能够实现零速重载启动与低速大扭矩运行,具有良好的动态特性;在负载发生突变时,系统2台永磁半直驱电机能够迅速响应,输出转速曲线基本一致,电磁转矩曲线与负载转矩曲线也基本一致,表明永磁电机半直驱系统具有良好的同步性能。在性能指标方面,永磁电机半直驱系统在全负载点功率因数均高达90%,传动效率均超过82%,对比传统异步电机驱动系统,传动效率至少提升了16.3%以上,显著提升了设备驱动性能与节电率。
2)通过机−电耦合模型仿真分析得到以下动力学行为规律:在启动瞬间与负载突变瞬间,刮板输送机链条的速度、加速度与张力会发生波动,链条具有明显的粘弹力学特性,在机头与机尾链轮处波动峰值最大;运行过程中链条的波动幅度与落煤量成正相关性,其中满载启动工况下链条的速度、加速度分别为空载启动的2倍、2.3倍,对系统的冲击更大,因此应尽量避免满载启动运行。
3)永磁电机半直驱系统的行星齿轮减速机构为两级行星轮系,在冲击载荷下,各级太阳轮、行星轮与内齿圈的扭转位移、弹性变形、与动态啮合力均会发生明显变化,而第二级行星轮系的变化要大于第一级;在同级传动中,行星轮与太阳轮之间的扭转位移要大于内齿圈与行星轮之间的所产生的,而行星轮与太阳轮之间的弹性变形与动态啮合力要小于内齿圈与行星轮之间的所产生的;以上动力学规律可为永磁电机半直驱系统的分析设计及可靠运行提供理论参考。
4)借助永磁电机半直驱刮板输送机机−电耦合动力学模型与试验平台,验证了新型永磁电机半直驱系统的技术可行性及其在驱动性能方面的节能优势,而目前针对永磁驱动技术的智能矢量控制策略是主要用于带式输送机等较为平缓的负载工况。为避免刮板输送机片帮、卡链与断链等故障对新型永磁电机半直驱动系统运行的影响,后期可引入模糊控制与自抗扰控制等先进算法来提高驱动系统抗干扰能力,保障电机持续高效运转。
-
表 1 SGZ1000/2000型刮板输送机主要参数
Table 1 Main parameters of SGZ1000/2000 scraper conveyor
参数 数值 运输距离/m 300 运量能力/(t·h−1) 2500 驱动系统形式 异步电机+液力耦合器+减速器 驱动电机功率/kW 2× 1000 链条型式 中双链 链规格/mm ø48×152 表 2 刮板输送机永磁电机半直驱系统关键参数
Table 2 Key parameters of permanent magnet motor semi-direct driving system for scraper conveyor
参数 数值 驱动系统形式 变频器+永磁半直驱电机 装机功率/kW 2× 1000 额定电流/A 185 额定电压/V 3300 额定转速/(r·min−1) 750 额定频率/Hz 50 减速机构传动比 15 压力角/(°) 20 模数 10 太阳轮齿数 20、23 行星轮齿数 19、22 表 3 机−电耦合动力学模型仿真参数
Table 3 Simulation parameters of electromechanical coupling dynamics model
参数 数值 定子电阻/Ω 0.0816 永磁体磁链/Wb 5.7 直轴电感/mH 10.2 交轴电感/mH 37.9 电机转动惯量/(kg·m2) 40 阻尼系数/(N·m·s) 0.005 系统额定转速/(r·min−1) 50 链条转速/(m·s−1) 2 表 4 冲击载荷下第二级齿轮扭转位移
Table 4 Second stage gear torsional displacement under impact load
参数名称 扭转位移量变化范围/m 太阳轮 3.0×10−4~9.2×10−4 行星轮 −1.0×10−4~−6.9×10−4 内齿圈 −2.1×10−4~−6.9×10−4 表 5 冲击载荷下行星齿轮传动系统弹性变形量
Table 5 Elastic deformation of planetary gear transmission system under impact load
参数名称 弹性变形量变化范围/m 第一级太阳轮与行星轮 1.8×10−4~4.4×10−4 第一级内齿圈和行星轮 1.5×10−4~6.1×10−4 第二级太阳轮与行星轮 3.8×10−4~7.9×10−4 第二级内齿圈与行星轮 3.5×10−4~12.3×10−4 表 6 冲击载荷下行星齿轮传动系统动态啮合力
Table 6 Dynamic meshing force of planetary gear transmission system under impact load
参数名称 动态啮合力变化范围/N 第一级太阳轮与行星轮 1.7×105~4.6×105 第一级内齿圈和行星轮 1.3×105~5.8×105 第二级太阳轮与行星轮 5.9×105~1.2×106 第二级内齿圈与行星轮 5.0×105~1.7×106 表 7 永磁电机半直驱系统试验平台参数
Table 7 Parameters of permanent magnet motor semi-direct driving system test platform
设备 型号 永磁同步电机 TYVZ-3800-280M-16 磁粉式测功机 4PB15 测功机控制器 DSP6001 二级齿轮减速器 ZLY160-8-1 扭矩传感器 TQ-660 数据采集卡 USB-7648A -
[1] 中矿(北京)煤炭产业景气指数研究课题组. 2022-2023年中国煤炭产业经济形势研究报告[J]. 中国煤炭,2023,49(3):2−10. doi: 10.3969/j.issn.1006-530X.2023.03.001 Research Group of Zhongkuang (Beijing) Coal Industry Prosperity Index. Research report on the economic situation of China's coal industry from 2022-2023[J]. China Coal,2023,49(3):2−10. doi: 10.3969/j.issn.1006-530X.2023.03.001
[2] 葛世荣,张晞,薛光辉,等. 我国煤矿煤机智能技术与装备发展研究[J]. 中国工程科学,2023,25(5):146−156. doi: 10.15302/J-SSCAE-2023.05.013 GE Shirong, ZHANG Xi, XUE Guanghui, et al. Development of intelligent technologies and machinery for coal mining in China’s underground coal mines[J]. Strategic Study of CAE,2023,25(5):146−156. doi: 10.15302/J-SSCAE-2023.05.013
[3] 葛世荣,郝尚清,张世洪,等. 我国智能化采煤技术现状及待突破关键技术[J]. 煤炭科学技术,2020,48(7):28−46. GE Shirong, HAO Shangqing, ZHANG Shihong, et al. Status of intelligent coal mining technology and potential key technologies in China[J]. Coal Science and Technology,2020,48(7):28−46.
[4] 鲍久圣,刘琴,葛世荣,等. 矿山运输装备智能化技术研究现状及发展趋势[J]. 智能矿山,2020,1(1):78−88. BAO Jiusheng, LIU Qin, GE Shirong, et al. Research status and development trend of intelligent technologies for mine transportation equipment[J]. Journal of Intelligent Mine,2020,1(1):78−88.
[5] 葛世荣. 刮板输送机技术发展历程(三):驱动与智能控制技术[J]. 中国煤炭,2024,50(4):1−12. GE Shirong. The development history of scraper conveyor technology (Part three):Intelligent drive and control technology[J]. China Coal,2024,50(4):1−12.
[6] LI L, CUI H W, LIAN Z S, et al. Modeling and optimization of soft start-up for hydroviscous drive applied to scraper conveyor[J]. Mathematical Problems in Engineering,2019,2019(1):6131364. doi: 10.1155/2019/6131364
[7] 井万里,贾立新,李梦毅,等. 刮板输送机双机驱动系统研究[J]. 工矿自动化,2022,48(4):72−77. JING Wanli, JIA Lixin, LI Mengyi, et al. A dual-motor drive system for scraper conveyor[J]. Journal of Mine Automation,2022,48(4):72−77.
[8] 张磊,鲍久圣,葛世荣,等. 永磁驱动技术及其在矿山装备领域的应用现状[J]. 煤炭科学技术,2022,50(3):275−284. ZHANG Lei, BAO Jiusheng, GE Shirong, et al. Permanent magnet driving technology and its application status in the field of mining equipment[J]. Coal Science and Technology,2022,50(3):275−284.
[9] 张磊,郝建伟,鲍久圣,等. 全永磁驱动带式输送机控制策略及动力学行为[J]. 机械工程学报,2022,58(21):134−147. doi: 10.3901/JME.2022.21.134 ZHANG Lei, HAO Jianwei, BAO Jiusheng, et al. Control strategy and dynamic behavior of full permanent magnet driving belt conveyor[J]. Journal of Mechanical Engineering,2022,58(21):134−147. doi: 10.3901/JME.2022.21.134
[10] 王雷,涂兴子,韩建国. 智能隔爆永磁同步滚筒:ZL201820302257.6 [P]. 2020−08−11. [11] 张务果. 采煤机截割部永磁短程驱动系统动态特性研究[D]. 徐州:中国矿业大学,2016. ZHANG Wuguo. Research on dynamic characteristics of permanent magnet short-range drive system for coal mining machine cutting section[D]. Xuzhou:China University of Mining and Technology, 2016.
[12] 姜耸,李威,王禹桥,等. 采煤机永磁半直驱截割传动系统动态特性研究[J]. 机械设计与制造,2024(9):97−103. doi: 10.3969/j.issn.1001-3997.2024.09.019 JIANG Song, LI Wei, WANG Yuqiao, et al. Study on dynamic characteristics of permanent magnet semi-direct drive cutting transmission system in shearer[J]. Machinery Design & Manufacture,2024(9):97−103. doi: 10.3969/j.issn.1001-3997.2024.09.019
[13] 王洋洋,鲍久圣,葛世荣,等. 刮板输送机永磁直驱系统机−电耦合模型仿真与试验[J]. 煤炭学报,2020,45(6):2127−2139. WANG Yangyang, BAO Jiusheng, GE Shirong, et al. Simulation and experimental study on electromechanical coupling model of permanent magnet direct drive system for scraper conveyor[J]. Journal of China Coal Society,2020,45(6):2127−2139.
[14] 鞠锦勇,李威,范孟豹,等. 永磁电机驱动的刮板输送机主传动系统机电耦合扭振动态分岔研究[J]. 振动与冲击,2018,37(23):52−60. JU Jinyong, LI Wei, FAN Mengbao, et al. Dynamic bifurcation analysis of electro-mechanical coupled torsional vibration for main transmission system of scraper conveyer driven by permanent magnet motor[J]. Journal of Vibration and Shock,2018,37(23):52−60.
[15] 张强,刘伟,王聪,等. 刮板输送机多永磁电机串联驱动新模式及关键技术[J]. 煤炭科学技术,2024,52(2):238−252. doi: 10.12438/cst.2023-1396 ZHANG Qiang, LIU Wei, WANG Cong, et al. New mode and key technology of series drive of multiple permanent magnet motors for scraper conveyor[J]. Coal Science and Technology,2024,52(2):238−252. doi: 10.12438/cst.2023-1396
[16] 葛世荣,鲍久圣,张磊. 一种并联永磁电机智能半直驱式刮板输送机:CN110752705B[P]. 2020-08-11. [17] 舒子龙. 永磁电机半直驱刮板输送机动态特性研究[D]. 徐州:中国矿业大学,2019. SHU Zilong. Research on dynamic characteristics of permanent magnet motor semi-direct drive scraper conveyor[D]. Xuzhou:China University of Mining and Technology, 2019.
[18] 单文桃,李坤. 内置式永磁同步电主轴模糊滑模联合矢量控制[J]. 机械工程学报,2022,58(3):177−185. doi: 10.3901/JME.2022.03.177 SHAN Wentao, LI Kun. SMC-FUZZY joint vector control of built-in permanent magnet synchronous motorized spindle[J]. Journal of Mechanical Engineering,2022,58(3):177−185. doi: 10.3901/JME.2022.03.177




 下载:
下载: